
Normal coordinates
Encyclopedia
In differential geometry, normal coordinates at a point p in a differentiable manifold
equipped with a symmetric
affine connection
are a local coordinate system in a neighborhood of p obtained by applying the exponential map
to the tangent space
at p. In a normal coordinate system, the Christoffel symbols
of the connection vanish at the point p, thus often simplifying local calculations. In normal coordinates associated to the Levi-Civita connection
of a Riemannian manifold
, one can additionally arrange that the metric tensor
is the Kronecker delta at the point p, and that the first partial derivative
s of the metric at p vanish.
A basic result of differential geometry states that normal coordinates at a point always exist on a manifold with a symmetric affine connection. In such coordinates the covariant derivative reduces to a partial derivative (at p only), and the geodesics through p are locally linear functions of t (the affine parameter). This idea was implemented in a fundamental way by Albert Einstein
in the general theory of relativity: the equivalence principle
uses normal coordinates via inertial frames. Normal coordinates always exist for the Levi-Civita connection of a Riemannian or Pseudo-Riemannian manifold. By contrast, there is no way to define normal coordinates for Finsler manifold
s .

and an isomorphism
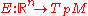
given by any basis of the tangent space at the fixed basepoint p ∈ M. If the additional structure of a Riemannian metric is imposed, then the basis defined by E may be required in addition to be orthonormal
, and the resulting coordinate system is then known as a Riemannian normal coordinate system.
Normal coordinates exist on a normal neighborhood of a point p in M. A normal neighborhood U is a subset of M such that there is a proper neighborhood V of the origin in the tangent space
TpM and expp acts as a diffeomorphism
between U and V. Now let U be a normal neighborhood of p in M then the chart is given by:

The isomorphism E can be any isomorphism between both vectorspaces, so there are as many charts as different orthonormal bases exist in the domain of E.
Polar coordinates provide a number of fundamental tools in Riemannian geometry. The radial coordinate is the most significant: geometrically it represents the geodesic distance to p of nearby points. Gauss's lemma
asserts that the gradient
of r is simply the partial derivative
 . That is,
. That is,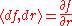
for any smooth function ƒ. As a result, the metric in polar coordinates assumes a block diagonal form
Differentiable manifold
A differentiable manifold is a type of manifold that is locally similar enough to a linear space to allow one to do calculus. Any manifold can be described by a collection of charts, also known as an atlas. One may then apply ideas from calculus while working within the individual charts, since...
equipped with a symmetric
Torsion tensor
In differential geometry, the notion of torsion is a manner of characterizing a twist or screw of a moving frame around a curve. The torsion of a curve, as it appears in the Frenet-Serret formulas, for instance, quantifies the twist of a curve about its tangent vector as the curve evolves In the...
affine connection
Affine connection
In the branch of mathematics called differential geometry, an affine connection is a geometrical object on a smooth manifold which connects nearby tangent spaces, and so permits tangent vector fields to be differentiated as if they were functions on the manifold with values in a fixed vector space...
are a local coordinate system in a neighborhood of p obtained by applying the exponential map
Exponential map
In differential geometry, the exponential map is a generalization of the ordinary exponential function of mathematical analysis to all differentiable manifolds with an affine connection....
to the tangent space
Tangent space
In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
at p. In a normal coordinate system, the Christoffel symbols
Christoffel symbols
In mathematics and physics, the Christoffel symbols, named for Elwin Bruno Christoffel , are numerical arrays of real numbers that describe, in coordinates, the effects of parallel transport in curved surfaces and, more generally, manifolds. As such, they are coordinate-space expressions for the...
of the connection vanish at the point p, thus often simplifying local calculations. In normal coordinates associated to the Levi-Civita connection
Levi-Civita connection
In Riemannian geometry, the Levi-Civita connection is a specific connection on the tangent bundle of a manifold. More specifically, it is the torsion-free metric connection, i.e., the torsion-free connection on the tangent bundle preserving a given Riemannian metric.The fundamental theorem of...
of a Riemannian manifold
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
, one can additionally arrange that the metric tensor
Metric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
is the Kronecker delta at the point p, and that the first partial derivative
Partial derivative
In mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant...
s of the metric at p vanish.
A basic result of differential geometry states that normal coordinates at a point always exist on a manifold with a symmetric affine connection. In such coordinates the covariant derivative reduces to a partial derivative (at p only), and the geodesics through p are locally linear functions of t (the affine parameter). This idea was implemented in a fundamental way by Albert Einstein
Albert Einstein
Albert Einstein was a German-born theoretical physicist who developed the theory of general relativity, effecting a revolution in physics. For this achievement, Einstein is often regarded as the father of modern physics and one of the most prolific intellects in human history...
in the general theory of relativity: the equivalence principle
Equivalence principle
In the physics of general relativity, the equivalence principle is any of several related concepts dealing with the equivalence of gravitational and inertial mass, and to Albert Einstein's assertion that the gravitational "force" as experienced locally while standing on a massive body is actually...
uses normal coordinates via inertial frames. Normal coordinates always exist for the Levi-Civita connection of a Riemannian or Pseudo-Riemannian manifold. By contrast, there is no way to define normal coordinates for Finsler manifold
Finsler manifold
In mathematics, particularly differential geometry, a Finsler manifold is a differentiable manifold together with the structure of an intrinsic quasimetric space in which the length of any rectifiable curve is given by the length functional...
s .
Geodesic normal coordinates
Geodesic normal coordinates are local coordinates on a manifold with an affine connection afforded by the exponential mapExponential map
In differential geometry, the exponential map is a generalization of the ordinary exponential function of mathematical analysis to all differentiable manifolds with an affine connection....

and an isomorphism
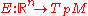
given by any basis of the tangent space at the fixed basepoint p ∈ M. If the additional structure of a Riemannian metric is imposed, then the basis defined by E may be required in addition to be orthonormal
Orthonormal basis
In mathematics, particularly linear algebra, an orthonormal basis for inner product space V with finite dimension is a basis for V whose vectors are orthonormal. For example, the standard basis for a Euclidean space Rn is an orthonormal basis, where the relevant inner product is the dot product of...
, and the resulting coordinate system is then known as a Riemannian normal coordinate system.
Normal coordinates exist on a normal neighborhood of a point p in M. A normal neighborhood U is a subset of M such that there is a proper neighborhood V of the origin in the tangent space
Tangent space
In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
TpM and expp acts as a diffeomorphism
Diffeomorphism
In mathematics, a diffeomorphism is an isomorphism in the category of smooth manifolds. It is an invertible function that maps one differentiable manifold to another, such that both the function and its inverse are smooth.- Definition :...
between U and V. Now let U be a normal neighborhood of p in M then the chart is given by:

The isomorphism E can be any isomorphism between both vectorspaces, so there are as many charts as different orthonormal bases exist in the domain of E.
Properties
The properties of normal coordinates often simplify computations. In the following, assume that U is a normal neighborhood centered at p in M and (xi) are normal coordinates on U.- Let V be some vector from TpM with components Vi in local coordinates, and
 be the geodesicGeodesicIn mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...
be the geodesicGeodesicIn mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...
with starting point p and velocity vector V, then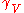 is represented in normal coordinates by
is represented in normal coordinates by  as long as it is in U.
as long as it is in U. - The coordinates of p are (0, ... , 0)
- In Riemannian normal coordinates at p the components of the Riemannian metricMetric tensorIn the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
g simplify to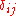 .
. - The Christoffel symbolsChristoffel symbolsIn mathematics and physics, the Christoffel symbols, named for Elwin Bruno Christoffel , are numerical arrays of real numbers that describe, in coordinates, the effects of parallel transport in curved surfaces and, more generally, manifolds. As such, they are coordinate-space expressions for the...
vanish at p. In the Riemannian case, so do the first partial derivatives of .
.
Polar coordinates
On a Riemannian manifold, a normal coordinate system at p facilitates the introduction of a system of spherical coordinates, known as polar coordinates. These are the coordinates on M obtained by introducing the standard spherical coordinate system on the Euclidean space TpM. That is, one introduces on TpM the standard spherical coordinate system (r,φ) where r ≥ 0 is the radial parameter and φ = (φ1,...,φn−1) is a parameterization of the (n−1)-sphere. Composition of (r,φ) with the inverse of the exponential map at p is a polar coordinate system.Polar coordinates provide a number of fundamental tools in Riemannian geometry. The radial coordinate is the most significant: geometrically it represents the geodesic distance to p of nearby points. Gauss's lemma
Gauss's lemma (Riemannian geometry)
In Riemannian geometry, Gauss's lemma asserts that any sufficiently small sphere centered at a point in a Riemannian manifold is perpendicular to every geodesic through the point. More formally, let M be a Riemannian manifold, equipped with its Levi-Civita connection, and p a point of M...
asserts that the gradient
Gradient
In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
of r is simply the partial derivative
Partial derivative
In mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant...
 . That is,
. That is,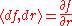
for any smooth function ƒ. As a result, the metric in polar coordinates assumes a block diagonal form


