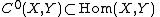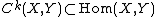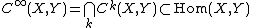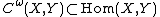Germ (mathematics)
Encyclopedia
In mathematics, the notion of a germ of an object in/on a topological space captures the local properties of the object. In particular, the objects in question are mostly functions (or maps
) and subsets. In specific implementations of this idea, the sets or maps in question will have specific properties, such as being analytic or smooth, but in general this is not needed (the maps or functions in question need not even be continuous); it is however necessary that the space on/in which the object is defined is a topological space, in order that the word local have some sense.
The name is derived from cereal germ
in a continuation of the sheaf
metaphor, as a germ is (locally) the "heart" of a function, as it is for a grain.
meaning that for all x in U.
Similarly, if S and T are any two subsets of X, then they define the same germ at x if there is again a neighbourhood U of x such that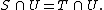
It is straightforward to see that defining the same germ at x is an equivalence relation
(be it on maps or sets), and the equivalence classes are called germs (map-germs, or set-germs accordingly). The equivalence relation is usually written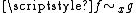 or
or 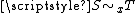 .
.
Given a map f on X, then its germ at x is usually denoted [f ]x. Similarly, the germ at x of a set S is written [S]x. Thus,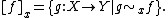
To denote a map germ at x in X which maps the point x in X to the point y in Y, one writes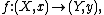
such an f is then an entire equivalence class of maps, and it is usual to use the same letter f for any representative map.
Notice that two sets are germ-equivalent at x if and only if their characteristic function
s are germ-equivalent at x: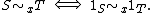
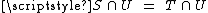 , and then moreover
, and then moreover 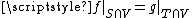 , for some smaller neighbourhood V with
, for some smaller neighbourhood V with 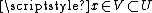 . This is particularly relevant in two settings:
. This is particularly relevant in two settings:
Moreover, if the target Y is a vector space, then it makes sense to add germs: to define [f]x + [g]x, first take representatives f and g, defined on neighbourhoods U and V respectively, then [f]x + [g]x is the germ at x of the map f + g (where f + g is defined on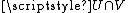 ).
).
(In the same way one can define more general linear combinations.)
The set of germs at x of maps from X to Y does not have a useful topology, except for the discrete one. It therefore makes little or no sense to talk of a convergent sequence of germs.
However, if X and Y are manifolds, then the spaces of jets
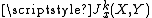 (finite order Taylor series at x of map(-germs)) do have topologies as they can be identified with finite-dimensional vector spaces.
(finite order Taylor series at x of map(-germs)) do have topologies as they can be identified with finite-dimensional vector spaces.
A presheaf
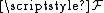 on a topological space X is an assignment of an Abelian group
on a topological space X is an assignment of an Abelian group
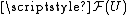 to each open set U in X. Typical examples of Abelian groups here are: real valued functions on U, differential forms on U, vector fields on U, holomorphic functions on U (when X is a complex space), constant functions on U and differential operators on U.
to each open set U in X. Typical examples of Abelian groups here are: real valued functions on U, differential forms on U, vector fields on U, holomorphic functions on U (when X is a complex space), constant functions on U and differential operators on U.
If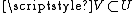 then there is a restriction map
then there is a restriction map 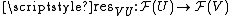 , satisfying certain compatibility conditions. For a fixed x, one says that elements
, satisfying certain compatibility conditions. For a fixed x, one says that elements 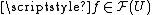 and
and 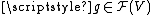 are equivalent at x if there is a neighbourhood
are equivalent at x if there is a neighbourhood 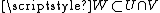 of x with resWU(f) = resWV(g) (both elements of
of x with resWU(f) = resWV(g) (both elements of 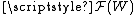 ). The equivalence classes form the stalk
). The equivalence classes form the stalk
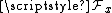 at x of the presheaf
at x of the presheaf 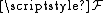 . This equivalence relation is an abstraction of the germ equivalence described above.
. This equivalence relation is an abstraction of the germ equivalence described above.
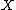 and
and 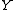 have additional structure, it is possible to define subsets of the set of all maps from X to Y or more generally sub-presheaves of a given presheaf
have additional structure, it is possible to define subsets of the set of all maps from X to Y or more generally sub-presheaves of a given presheaf 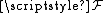 and corresponding germs: some notable examples follow.
and corresponding germs: some notable examples follow.
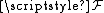 on a topological space
on a topological space 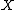 at a point
at a point  of
of 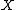 is commonly denoted by
is commonly denoted by 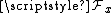 . As a consequence germs, being stalks of sheaves of various kind of functions, borrow this scheme of notation:
. As a consequence germs, being stalks of sheaves of various kind of functions, borrow this scheme of notation:
For germs of sets and varieties, the notation is not so well established: some notations found in literature include:
When the point is fixed and known (e.g. when
is fixed and known (e.g. when 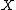 is a topological vector space
is a topological vector space
and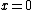 ), it can be dropped in each of the above symbols: also, when dim
), it can be dropped in each of the above symbols: also, when dim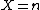 , a subscript before the symbol can be added. As example
, a subscript before the symbol can be added. As example
of a function at a point can be studied analyzing its germ. They are a generalization of Taylor series
, and indeed the Taylor series of a germ (of a differentiable function) is defined: you only need local information to compute derivatives.
Germs are useful in determining the properties of dynamical systems
near chosen points of their phase space
: they are one of the main tools in singularity theory
and catastrophe theory
.
When the topological spaces considered are Riemann surface
s or more generally analytic varieties
, germs of holomorphic functions on them can be viewed as power series, and thus the set of germs can be considered to be the analytic continuation
of an analytic function
.
Map (mathematics)
In most of mathematics and in some related technical fields, the term mapping, usually shortened to map, is either a synonym for function, or denotes a particular kind of function which is important in that branch, or denotes something conceptually similar to a function.In graph theory, a map is a...
) and subsets. In specific implementations of this idea, the sets or maps in question will have specific properties, such as being analytic or smooth, but in general this is not needed (the maps or functions in question need not even be continuous); it is however necessary that the space on/in which the object is defined is a topological space, in order that the word local have some sense.
The name is derived from cereal germ
Cereal germ
The germ of a cereal is the reproductive part that germinates to grow into a plant; it is the embryo of the seed. Along with bran, germ is often a by-product of the milling that produces refined grain products. Cereal grains and their components, such as wheat germ, rice bran, and maize may be used...
in a continuation of the sheaf
Sheaf (mathematics)
In mathematics, a sheaf is a tool for systematically tracking locally defined data attached to the open sets of a topological space. The data can be restricted to smaller open sets, and the data assigned to an open set is equivalent to all collections of compatible data assigned to collections of...
metaphor, as a germ is (locally) the "heart" of a function, as it is for a grain.
Basic definition
Given a point x of a topological space X, and two maps f, g : X → Y (where Y is any set), then f and g define the same germ at x if there is a neighbourhood U of x such that restricted to U, f and g are equal;meaning that for all x in U.
Similarly, if S and T are any two subsets of X, then they define the same germ at x if there is again a neighbourhood U of x such that
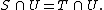
It is straightforward to see that defining the same germ at x is an equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
(be it on maps or sets), and the equivalence classes are called germs (map-germs, or set-germs accordingly). The equivalence relation is usually written
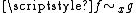 or
or 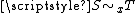 .
.Given a map f on X, then its germ at x is usually denoted [f ]x. Similarly, the germ at x of a set S is written [S]x. Thus,
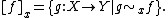
To denote a map germ at x in X which maps the point x in X to the point y in Y, one writes
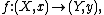
such an f is then an entire equivalence class of maps, and it is usual to use the same letter f for any representative map.
Notice that two sets are germ-equivalent at x if and only if their characteristic function
Characteristic function
In mathematics, characteristic function can refer to any of several distinct concepts:* The most common and universal usage is as a synonym for indicator function, that is the function* In probability theory, the characteristic function of any probability distribution on the real line is given by...
s are germ-equivalent at x:
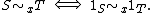
More generally
Maps need not be defined on all of X, and in particular they don't need to have the same domain. However, if f has domain S and g has domain T, both subsets of X, then f and g are germ equivalent at x in X if first S and T are germ equivalent at x, say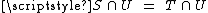 , and then moreover
, and then moreover 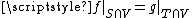 , for some smaller neighbourhood V with
, for some smaller neighbourhood V with 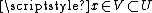 . This is particularly relevant in two settings:
. This is particularly relevant in two settings:
- f is defined on a subvariety V of X, and
- f has a pole of some sort at x, so is not even defined at x, as for example a rational function, which would be defined off a subvariety.
Basic properties
If f and g are germ equivalent at x, then they share all local properties, such as continuity, differentiability etc., so it makes sense to talk about a differentiable or analytic germ, etc. Similarly for subsets: if one representative of a germ is an analytic set then so are all representatives, at least on some neighbourhood of x.Moreover, if the target Y is a vector space, then it makes sense to add germs: to define [f]x + [g]x, first take representatives f and g, defined on neighbourhoods U and V respectively, then [f]x + [g]x is the germ at x of the map f + g (where f + g is defined on
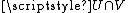 ).
).(In the same way one can define more general linear combinations.)
The set of germs at x of maps from X to Y does not have a useful topology, except for the discrete one. It therefore makes little or no sense to talk of a convergent sequence of germs.
However, if X and Y are manifolds, then the spaces of jets
Jet (mathematics)
In mathematics, the jet is an operation which takes a differentiable function f and produces a polynomial, the truncated Taylor polynomial of f, at each point of its domain...
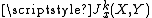 (finite order Taylor series at x of map(-germs)) do have topologies as they can be identified with finite-dimensional vector spaces.
(finite order Taylor series at x of map(-germs)) do have topologies as they can be identified with finite-dimensional vector spaces.Relation with sheaves
The idea of germ is behind the definition of sheaves and presheaves.A presheaf
Sheaf (mathematics)
In mathematics, a sheaf is a tool for systematically tracking locally defined data attached to the open sets of a topological space. The data can be restricted to smaller open sets, and the data assigned to an open set is equivalent to all collections of compatible data assigned to collections of...
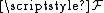 on a topological space X is an assignment of an Abelian group
on a topological space X is an assignment of an Abelian groupAbelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
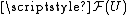 to each open set U in X. Typical examples of Abelian groups here are: real valued functions on U, differential forms on U, vector fields on U, holomorphic functions on U (when X is a complex space), constant functions on U and differential operators on U.
to each open set U in X. Typical examples of Abelian groups here are: real valued functions on U, differential forms on U, vector fields on U, holomorphic functions on U (when X is a complex space), constant functions on U and differential operators on U.If
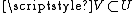 then there is a restriction map
then there is a restriction map 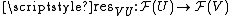 , satisfying certain compatibility conditions. For a fixed x, one says that elements
, satisfying certain compatibility conditions. For a fixed x, one says that elements 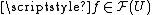 and
and 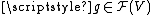 are equivalent at x if there is a neighbourhood
are equivalent at x if there is a neighbourhood 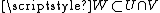 of x with resWU(f) = resWV(g) (both elements of
of x with resWU(f) = resWV(g) (both elements of 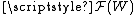 ). The equivalence classes form the stalk
). The equivalence classes form the stalkStalk (sheaf)
The stalk of a sheaf is a mathematical construction capturing the behaviour of a sheaf around a given point.-Motivation and definition:Sheaves are defined on open sets, but the underlying topological space X consists of points. It is reasonable to attempt to isolate the behavior of a sheaf at a...
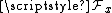 at x of the presheaf
at x of the presheaf 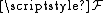 . This equivalence relation is an abstraction of the germ equivalence described above.
. This equivalence relation is an abstraction of the germ equivalence described above.Examples
If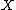 and
and 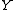 have additional structure, it is possible to define subsets of the set of all maps from X to Y or more generally sub-presheaves of a given presheaf
have additional structure, it is possible to define subsets of the set of all maps from X to Y or more generally sub-presheaves of a given presheaf 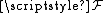 and corresponding germs: some notable examples follow.
and corresponding germs: some notable examples follow.- If
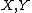 are both topological spaces, the subset
are both topological spaces, the subset
-
- of continuous functionContinuous functionIn mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
s defines germs of continuous functions.- If both
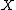 and
and 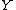 admit a differentiable structure, the subsetSubsetIn mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
admit a differentiable structure, the subsetSubsetIn mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
- If both
- of
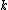 -times continuously differentiable functionDifferentiable functionIn calculus , a differentiable function is a function whose derivative exists at each point in its domain. The graph of a differentiable function must have a non-vertical tangent line at each point in its domain...
-times continuously differentiable functionDifferentiable functionIn calculus , a differentiable function is a function whose derivative exists at each point in its domain. The graph of a differentiable function must have a non-vertical tangent line at each point in its domain...
s, the subsetSubsetIn mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
- of smooth functionSmooth functionIn mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
s and the subsetSubsetIn mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
- of analytic functionAnalytic functionIn mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
s can be defined (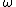 here is the ordinalOrdinal numberIn set theory, an ordinal number, or just ordinal, is the order type of a well-ordered set. They are usually identified with hereditarily transitive sets. Ordinals are an extension of the natural numbers different from integers and from cardinals...
here is the ordinalOrdinal numberIn set theory, an ordinal number, or just ordinal, is the order type of a well-ordered set. They are usually identified with hereditarily transitive sets. Ordinals are an extension of the natural numbers different from integers and from cardinals...
for infinity; this is an abuse of notationAbuse of notationIn mathematics, abuse of notation occurs when an author uses a mathematical notation in a way that is not formally correct but that seems likely to simplify the exposition or suggest the correct intuition . Abuse of notation should be contrasted with misuse of notation, which should be avoided...
, by analogy with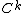 and
and 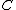 ∞), and then spaces of germs of (finitely) differentiable, smooth, analytic functions can be constructed.
∞), and then spaces of germs of (finitely) differentiable, smooth, analytic functions can be constructed.
- If
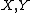 have a complex structure (for instance, are subsets of complex vector spacesVector spaceA vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
have a complex structure (for instance, are subsets of complex vector spacesVector spaceA vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
), holomorphic functionHolomorphic functionIn mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
s between them can be defined, and therefore spaces of germs of holomorphic functions can be constructed.
- If
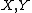 have an algebraic structureAlgebraic structureIn abstract algebra, an algebraic structure consists of one or more sets, called underlying sets or carriers or sorts, closed under one or more operations, satisfying some axioms. Abstract algebra is primarily the study of algebraic structures and their properties...
have an algebraic structureAlgebraic structureIn abstract algebra, an algebraic structure consists of one or more sets, called underlying sets or carriers or sorts, closed under one or more operations, satisfying some axioms. Abstract algebra is primarily the study of algebraic structures and their properties...
, then regularRegular functionIn mathematics, a regular function is a function that is analytic and single-valued in a given region. In complex analysis, any complex regular function is known as a holomorphic function...
(and rationalRational functionIn mathematics, a rational function is any function which can be written as the ratio of two polynomial functions. Neither the coefficients of the polynomials nor the values taken by the function are necessarily rational.-Definitions:...
) functions between them can be defined, and germs of regular functions (and likewise rational) can be defined.
Notation
The stalk of a sheaf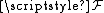 on a topological space
on a topological space 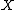 at a point
at a point  of
of 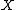 is commonly denoted by
is commonly denoted by 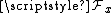 . As a consequence germs, being stalks of sheaves of various kind of functions, borrow this scheme of notation:
. As a consequence germs, being stalks of sheaves of various kind of functions, borrow this scheme of notation:
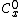 is the space of germs of continuous functions at
is the space of germs of continuous functions at  .
.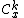 for each natural numberNatural numberIn mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
for each natural numberNatural numberIn mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
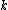 is the space of germs of
is the space of germs of 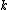 -times-differentiable functions at
-times-differentiable functions at  .
.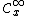 is the space of germs of infinitely differentiable ("smooth") functions at
is the space of germs of infinitely differentiable ("smooth") functions at  .
.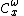 is the space of germs of analytic functions at
is the space of germs of analytic functions at  .
.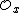 is the space of germs of holomorphic functions (in complex geometry), or space of germs of regular functions (in algebraic geometry) at
is the space of germs of holomorphic functions (in complex geometry), or space of germs of regular functions (in algebraic geometry) at  .
.
For germs of sets and varieties, the notation is not so well established: some notations found in literature include:
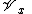 is the space of germs of analytic varieties at
is the space of germs of analytic varieties at  .
.
When the point
 is fixed and known (e.g. when
is fixed and known (e.g. when 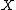 is a topological vector space
is a topological vector spaceTopological vector space
In mathematics, a topological vector space is one of the basic structures investigated in functional analysis...
and
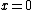 ), it can be dropped in each of the above symbols: also, when dim
), it can be dropped in each of the above symbols: also, when dim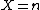 , a subscript before the symbol can be added. As example
, a subscript before the symbol can be added. As example
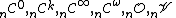 are the spaces of germs shown above when
are the spaces of germs shown above when 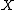 is a
is a  -dimensional vector spaceVector spaceA vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
-dimensional vector spaceVector spaceA vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
and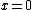 .
.
Applications
The key word in the applications of germs is locality: all local propertiesLocal property
In mathematics, a phenomenon is sometimes said to occur locally if, roughly speaking, it occurs on sufficiently small or arbitrarily small neighborhoods of points.-Properties of a single space:...
of a function at a point can be studied analyzing its germ. They are a generalization of Taylor series
Taylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
, and indeed the Taylor series of a germ (of a differentiable function) is defined: you only need local information to compute derivatives.
Germs are useful in determining the properties of dynamical systems
Dynamical system (definition)
The dynamical system concept is a mathematical formalization for any fixed "rule" which describes the time dependence of a point's position in its ambient space...
near chosen points of their phase space
Phase space
In mathematics and physics, a phase space, introduced by Willard Gibbs in 1901, is a space in which all possible states of a system are represented, with each possible state of the system corresponding to one unique point in the phase space...
: they are one of the main tools in singularity theory
Singularity theory
-The notion of singularity:In mathematics, singularity theory is the study of the failure of manifold structure. A loop of string can serve as an example of a one-dimensional manifold, if one neglects its width. What is meant by a singularity can be seen by dropping it on the floor...
and catastrophe theory
Catastrophe theory
In mathematics, catastrophe theory is a branch of bifurcation theory in the study of dynamical systems; it is also a particular special case of more general singularity theory in geometry....
.
When the topological spaces considered are Riemann surface
Riemann surface
In mathematics, particularly in complex analysis, a Riemann surface, first studied by and named after Bernhard Riemann, is a one-dimensional complex manifold. Riemann surfaces can be thought of as "deformed versions" of the complex plane: locally near every point they look like patches of the...
s or more generally analytic varieties
Analytic variety
In mathematics, specifically geometry, an analytic variety is defined locally as the set of common zeros of finitely many analytic functions. It is analogous to the included concept of complex algebraic variety, and every complex manifold is an analytic variety. Since analytic varieties may have...
, germs of holomorphic functions on them can be viewed as power series, and thus the set of germs can be considered to be the analytic continuation
Analytic continuation
In complex analysis, a branch of mathematics, analytic continuation is a technique to extend the domain of a given analytic function. Analytic continuation often succeeds in defining further values of a function, for example in a new region where an infinite series representation in terms of which...
of an analytic function
Analytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
.
See also
- Analytic varietyAnalytic varietyIn mathematics, specifically geometry, an analytic variety is defined locally as the set of common zeros of finitely many analytic functions. It is analogous to the included concept of complex algebraic variety, and every complex manifold is an analytic variety. Since analytic varieties may have...
- Catastrophe theoryCatastrophe theoryIn mathematics, catastrophe theory is a branch of bifurcation theory in the study of dynamical systems; it is also a particular special case of more general singularity theory in geometry....
- Gluing axiomGluing axiomIn mathematics, the gluing axiom is introduced to define what a sheaf F on a topological space X must satisfy, given that it is a presheaf, which is by definition a contravariant functor...
- Riemann surfaceRiemann surfaceIn mathematics, particularly in complex analysis, a Riemann surface, first studied by and named after Bernhard Riemann, is a one-dimensional complex manifold. Riemann surfaces can be thought of as "deformed versions" of the complex plane: locally near every point they look like patches of the...
- SheafSheaf (mathematics)In mathematics, a sheaf is a tool for systematically tracking locally defined data attached to the open sets of a topological space. The data can be restricted to smaller open sets, and the data assigned to an open set is equivalent to all collections of compatible data assigned to collections of...
- StalkStalk (sheaf)The stalk of a sheaf is a mathematical construction capturing the behaviour of a sheaf around a given point.-Motivation and definition:Sheaves are defined on open sets, but the underlying topological space X consists of points. It is reasonable to attempt to isolate the behavior of a sheaf at a...
External links
- Dorota Mozyrska, Zbigniew Bartosiewicz"Systems of germs and theorems of zeros in infinite-dimensional spaces", arxiv.org e-Prints server (Primary site at Cornell University). A research preprint dealing with germs of analytic varietiesAnalytic varietyIn mathematics, specifically geometry, an analytic variety is defined locally as the set of common zeros of finitely many analytic functions. It is analogous to the included concept of complex algebraic variety, and every complex manifold is an analytic variety. Since analytic varieties may have...
in an infinite dimensional setting.