
Catastrophe theory
Encyclopedia
In mathematics
, catastrophe theory is a branch of bifurcation theory
in the study of dynamical system
s; it is also a particular special case of more general singularity theory
in geometry
.
Bifurcation theory studies and classifies phenomena characterized by sudden shifts in behavior arising from small changes in circumstances, analysing how the qualitative nature of equation solutions depends on the parameters that appear in the equation. This may lead to sudden and dramatic changes, for example the unpredictable timing and magnitude
of a landslide
.
Catastrophe theory, which originated with the work of the French mathematician René Thom
in the 1960s, and became very popular due to the efforts of Christopher Zeeman in the 1970s, considers the special case where the long-run stable equilibrium can be identified with the minimum of a smooth, well-defined potential
function (Lyapunov function
).
Small changes in certain parameters of a nonlinear system can cause equilibria to appear or disappear, or to change from attracting to repelling and vice versa, leading to large and sudden changes of the behaviour of the system. However, examined in a larger parameter space, catastrophe theory reveals that such bifurcation points tend to occur as part of well-defined qualitative geometrical structures.
of the catastrophe geometries. The degeneracy of these critical points can be unfolded by expanding the potential function as a Taylor series
in small perturbations of the parameters.
When the degenerate points are not merely accidental, but are structurally stable
, the degenerate points exist as organising centres for particular geometric structures of lower degeneracy, with critical features in the parameter space around them. If the potential function depends on two or fewer active variables, and four (resp. five) or fewer active parameters, then there are only seven (resp. eleven) generic structures for these bifurcation geometries, with corresponding standard forms into which the Taylor series around the catastrophe germs can be transformed by diffeomorphism
(a smooth transformation whose inverse is also smooth). These seven fundamental types are now presented, with the names that Thom gave them.


At negative values of a, the potential has two extrema - one stable, and one unstable. If the parameter a is slowly increased, the system can follow the stable minimum point. But at the stable and unstable extrema meet, and annihilate. This is the bifurcation point. At there is no longer a stable solution. If a physical system is followed through a fold bifurcation, one therefore finds that as a reaches 0, the stability of the solution is suddenly lost, and the system will make a sudden transition to a new, very different behaviour. This bifurcation value of the parameter a is sometimes called the tipping point
.

The cusp geometry is very common, when one explores what happens to a fold bifurcation if a second parameter, b, is added to the control space. Varying the parameters, one finds that there is now a curve (blue) of points in (a,b) space where stability is lost, where the stable solution will suddenly jump to an alternate outcome.
But in a cusp geometry the bifurcation curve loops back on itself, giving a second branch where this alternate solution itself loses stability, and will make a jump back to the original solution set. By repeatedly increasing b and then decreasing it, one can therefore observe hysteresis
loops, as the system alternately follows one solution, jumps to the other, follows the other back, then jumps back to the first.
However, this is only possible in the region of parameter space . As a is increased, the hysteresis loops become smaller and smaller, until above they disappear altogether (the cusp catastrophe), and there is only one stable solution.
One can also consider what happens if one holds b constant and varies a. In the symmetrical case , one observes a pitchfork bifurcation
as a is reduced, with one stable solution suddenly splitting into two stable solutions and one unstable solution as the physical system passes to through the cusp point (0,0) (an example of spontaneous symmetry breaking
). Away from the cusp point, there is no sudden change in a physical solution being followed: when passing through the curve of fold bifurcations, all that happens is an alternate second solution becomes available.
A famous suggestion is that the cusp catastrophe can be used to model the behaviour of a stressed dog, which may respond by becoming cowed or becoming angry. The suggestion is that at moderate stress , the dog will exhibit a smooth transition of response from cowed to angry, depending on how it is provoked. But higher stress levels correspond to moving to the region . Then, if the dog starts cowed, it will remain cowed as it is irritated more and more, until it reaches the 'fold' point, when it will suddenly, discontinuously snap through to angry mode. Once in 'angry' mode, it will remain angry, even if the direct irritation parameter is considerably reduced.
Catastrophic failure of a complex system with parallel redundancy can be evaluated based on relationship between local and external stresses. The model of the structural fracture mechanics
is similar to the cusp catastrophe behavior. The model predicts reserve ability of a complex system.
Another application example is for the outer sphere electron transfer
frequently encountered in chemical and biological systems (Xu, F. Application of catastrophe theory to the ∆G≠ to -∆G relationship in electron transfer reactions. Zeitschrift für Physikalische Chemie Neue Folge 166, 79-91 (1990)).
Fold bifurcations and the cusp geometry are by far the most important practical consequences of catastrophe theory. They are patterns which reoccur again and again in physics, engineering and mathematical modelling.
They are the only way we currently have of detecting black holes and the dark matter
of the universe, via the phenomenon of gravitational lensing producing multiple images of distant quasars.
The remaining simple catastrophe geometries are very specialised in comparison, and presented here only for curiosity value.

The control parameter space is three dimensional. The bifurcation set in parameter space is made up of three surfaces of fold bifurcations, which meet in two lines of cusp bifurcations, which in turn meet at a single swallowtail bifurcation point.
As the parameters go through the surface of fold bifurcations, one minimum and one maximum of the potential function disappear. At the cusp bifurcations, two minima and one maximum are replaced by one minimum; beyond them the fold bifurcations disappear. At the swallowtail point, two minima and two maxima all meet at a single value of x. For values of a>0, beyond the swallowtail, there is either one maximum-minimum pair, or none at all, depending on the values of b and c. Two of the surfaces of fold bifurcations, and the two lines of cusp bifurcations where they meet for a<0, therefore disappear at the swallowtail point, to be replaced with only a single surface of fold bifurcations remaining. Salvador Dalí's
last painting, The Swallow's Tail
, was based on this catastrophe.

Depending on the parameter values, the potential function may have three, two, or one different local minima, separated by the loci of fold bifurcations. At the butterfly point, the different 3-surfaces of fold bifurcations, the 2-surfaces of cusp bifurcations, and the lines of swallowtail bifurcations all meet up and disappear, leaving a single cusp structure remaining when a>0
in the focal surfaces created by light reflecting off a surface in three dimensions and are intimately connected with the geometry of nearly spherical surfaces.
Thom proposed that the Hyperbolic umbilic catastrophe modeled the breaking of a wave and the elliptical umbilic modeled the creation of hair like structures.

gave the catastrophes the ADE classification
, due to a deep connection with simple Lie group
s.
There are objects in singularity theory which correspond to most of the other simple Lie groups.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, catastrophe theory is a branch of bifurcation theory
Bifurcation theory
Bifurcation theory is the mathematical study of changes in the qualitative or topological structure of a given family, such as the integral curves of a family of vector fields, and the solutions of a family of differential equations...
in the study of dynamical system
Dynamical system
A dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
s; it is also a particular special case of more general singularity theory
Singularity theory
-The notion of singularity:In mathematics, singularity theory is the study of the failure of manifold structure. A loop of string can serve as an example of a one-dimensional manifold, if one neglects its width. What is meant by a singularity can be seen by dropping it on the floor...
in geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
.
Bifurcation theory studies and classifies phenomena characterized by sudden shifts in behavior arising from small changes in circumstances, analysing how the qualitative nature of equation solutions depends on the parameters that appear in the equation. This may lead to sudden and dramatic changes, for example the unpredictable timing and magnitude
Magnitude (mathematics)
The magnitude of an object in mathematics is its size: a property by which it can be compared as larger or smaller than other objects of the same kind; in technical terms, an ordering of the class of objects to which it belongs....
of a landslide
Landslide
A landslide or landslip is a geological phenomenon which includes a wide range of ground movement, such as rockfalls, deep failure of slopes and shallow debris flows, which can occur in offshore, coastal and onshore environments...
.
Catastrophe theory, which originated with the work of the French mathematician René Thom
René Thom
René Frédéric Thom was a French mathematician. He made his reputation as a topologist, moving on to aspects of what would be called singularity theory; he became world-famous among the wider academic community and the educated general public for one aspect of this latter interest, his work as...
in the 1960s, and became very popular due to the efforts of Christopher Zeeman in the 1970s, considers the special case where the long-run stable equilibrium can be identified with the minimum of a smooth, well-defined potential
Scalar potential
A scalar potential is a fundamental concept in vector analysis and physics . The scalar potential is an example of a scalar field...
function (Lyapunov function
Lyapunov function
In the theory of ordinary differential equations , Lyapunov functions are scalar functions that may be used to prove the stability of an equilibrium of an ODE. Named after the Russian mathematician Aleksandr Mikhailovich Lyapunov, Lyapunov functions are important to stability theory and control...
).
Small changes in certain parameters of a nonlinear system can cause equilibria to appear or disappear, or to change from attracting to repelling and vice versa, leading to large and sudden changes of the behaviour of the system. However, examined in a larger parameter space, catastrophe theory reveals that such bifurcation points tend to occur as part of well-defined qualitative geometrical structures.
Elementary catastrophes
Catastrophe theory analyses degenerate critical points of the potential function — points where not just the first derivative, but one or more higher derivatives of the potential function are also zero. These are called the germsGerm (mathematics)
In mathematics, the notion of a germ of an object in/on a topological space captures the local properties of the object. In particular, the objects in question are mostly functions and subsets...
of the catastrophe geometries. The degeneracy of these critical points can be unfolded by expanding the potential function as a Taylor series
Taylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
in small perturbations of the parameters.
When the degenerate points are not merely accidental, but are structurally stable
Structural stability
In mathematics, structural stability is a fundamental property of a dynamical system which means that the qualitative behavior of the trajectories is unaffected by C1-small perturbations....
, the degenerate points exist as organising centres for particular geometric structures of lower degeneracy, with critical features in the parameter space around them. If the potential function depends on two or fewer active variables, and four (resp. five) or fewer active parameters, then there are only seven (resp. eleven) generic structures for these bifurcation geometries, with corresponding standard forms into which the Taylor series around the catastrophe germs can be transformed by diffeomorphism
Diffeomorphism
In mathematics, a diffeomorphism is an isomorphism in the category of smooth manifolds. It is an invertible function that maps one differentiable manifold to another, such that both the function and its inverse are smooth.- Definition :...
(a smooth transformation whose inverse is also smooth). These seven fundamental types are now presented, with the names that Thom gave them.
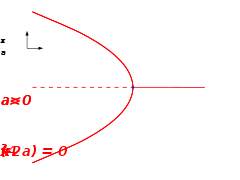
Fold catastrophe


At negative values of a, the potential has two extrema - one stable, and one unstable. If the parameter a is slowly increased, the system can follow the stable minimum point. But at the stable and unstable extrema meet, and annihilate. This is the bifurcation point. At there is no longer a stable solution. If a physical system is followed through a fold bifurcation, one therefore finds that as a reaches 0, the stability of the solution is suddenly lost, and the system will make a sudden transition to a new, very different behaviour. This bifurcation value of the parameter a is sometimes called the tipping point
Tipping point
In sociology, a tipping point is the event of a previously rare phenomenon becoming rapidly and dramatically more common. The phrase was coined in its sociological use by Morton Grodzins, by analogy with the fact in physics that adding a small amount of weight to a balanced object can cause it to...
.
Cusp catastrophe

 | |
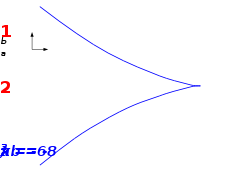 |  |
The cusp geometry is very common, when one explores what happens to a fold bifurcation if a second parameter, b, is added to the control space. Varying the parameters, one finds that there is now a curve (blue) of points in (a,b) space where stability is lost, where the stable solution will suddenly jump to an alternate outcome.
But in a cusp geometry the bifurcation curve loops back on itself, giving a second branch where this alternate solution itself loses stability, and will make a jump back to the original solution set. By repeatedly increasing b and then decreasing it, one can therefore observe hysteresis
Hysteresis
Hysteresis is the dependence of a system not just on its current environment but also on its past. This dependence arises because the system can be in more than one internal state. To predict its future evolution, either its internal state or its history must be known. If a given input alternately...
loops, as the system alternately follows one solution, jumps to the other, follows the other back, then jumps back to the first.
However, this is only possible in the region of parameter space . As a is increased, the hysteresis loops become smaller and smaller, until above they disappear altogether (the cusp catastrophe), and there is only one stable solution.
One can also consider what happens if one holds b constant and varies a. In the symmetrical case , one observes a pitchfork bifurcation
Pitchfork bifurcation
In bifurcation theory, a field within mathematics, a pitchfork bifurcation is a particular type of local bifurcation. Pitchfork bifurcations, like Hopf bifurcations have two types - supercritical or subcritical....
as a is reduced, with one stable solution suddenly splitting into two stable solutions and one unstable solution as the physical system passes to through the cusp point (0,0) (an example of spontaneous symmetry breaking
Spontaneous symmetry breaking
Spontaneous symmetry breaking is the process by which a system described in a theoretically symmetrical way ends up in an apparently asymmetric state....
). Away from the cusp point, there is no sudden change in a physical solution being followed: when passing through the curve of fold bifurcations, all that happens is an alternate second solution becomes available.
A famous suggestion is that the cusp catastrophe can be used to model the behaviour of a stressed dog, which may respond by becoming cowed or becoming angry. The suggestion is that at moderate stress , the dog will exhibit a smooth transition of response from cowed to angry, depending on how it is provoked. But higher stress levels correspond to moving to the region . Then, if the dog starts cowed, it will remain cowed as it is irritated more and more, until it reaches the 'fold' point, when it will suddenly, discontinuously snap through to angry mode. Once in 'angry' mode, it will remain angry, even if the direct irritation parameter is considerably reduced.
Catastrophic failure of a complex system with parallel redundancy can be evaluated based on relationship between local and external stresses. The model of the structural fracture mechanics
Structural Fracture Mechanics
Structural Fracture Mechanics is the field of structural engineering concerned with the study of load-carrying structures that includes one or several failed or damaged components...
is similar to the cusp catastrophe behavior. The model predicts reserve ability of a complex system.
Another application example is for the outer sphere electron transfer
Outer sphere electron transfer
Outer sphere refers to an electron transfer event that occurs between chemical species that remain separate intact before, during, and after the ET event. In contrast, for inner sphere electron transfer the participating redox sites undergoing ET become connected by a chemical bridge...
frequently encountered in chemical and biological systems (Xu, F. Application of catastrophe theory to the ∆G≠ to -∆G relationship in electron transfer reactions. Zeitschrift für Physikalische Chemie Neue Folge 166, 79-91 (1990)).
Fold bifurcations and the cusp geometry are by far the most important practical consequences of catastrophe theory. They are patterns which reoccur again and again in physics, engineering and mathematical modelling.
They are the only way we currently have of detecting black holes and the dark matter
Dark matter
In astronomy and cosmology, dark matter is matter that neither emits nor scatters light or other electromagnetic radiation, and so cannot be directly detected via optical or radio astronomy...
of the universe, via the phenomenon of gravitational lensing producing multiple images of distant quasars.
The remaining simple catastrophe geometries are very specialised in comparison, and presented here only for curiosity value.
Swallowtail catastrophe

The control parameter space is three dimensional. The bifurcation set in parameter space is made up of three surfaces of fold bifurcations, which meet in two lines of cusp bifurcations, which in turn meet at a single swallowtail bifurcation point.
As the parameters go through the surface of fold bifurcations, one minimum and one maximum of the potential function disappear. At the cusp bifurcations, two minima and one maximum are replaced by one minimum; beyond them the fold bifurcations disappear. At the swallowtail point, two minima and two maxima all meet at a single value of x. For values of a>0, beyond the swallowtail, there is either one maximum-minimum pair, or none at all, depending on the values of b and c. Two of the surfaces of fold bifurcations, and the two lines of cusp bifurcations where they meet for a<0, therefore disappear at the swallowtail point, to be replaced with only a single surface of fold bifurcations remaining. Salvador Dalí's
Salvador Dalí
Salvador Domènec Felip Jacint Dalí i Domènech, Marquis de Púbol , commonly known as Salvador Dalí , was a prominent Spanish Catalan surrealist painter born in Figueres,Spain....
last painting, The Swallow's Tail
The Swallow's Tail
The Swallow's Tail — Series on Catastrophes was Salvador Dalí's last painting. It was completed in May 1983, as the final part of a series based on René Thom's catastrophe theory....
, was based on this catastrophe.
Butterfly catastrophe

Depending on the parameter values, the potential function may have three, two, or one different local minima, separated by the loci of fold bifurcations. At the butterfly point, the different 3-surfaces of fold bifurcations, the 2-surfaces of cusp bifurcations, and the lines of swallowtail bifurcations all meet up and disappear, leaving a single cusp structure remaining when a>0
Potential functions of two active variables
Umbilic catastrophes are examples of corank 2 catastrophes. They can be observed in opticsOptics
Optics is the branch of physics which involves the behavior and properties of light, including its interactions with matter and the construction of instruments that use or detect it. Optics usually describes the behavior of visible, ultraviolet, and infrared light...
in the focal surfaces created by light reflecting off a surface in three dimensions and are intimately connected with the geometry of nearly spherical surfaces.
Thom proposed that the Hyperbolic umbilic catastrophe modeled the breaking of a wave and the elliptical umbilic modeled the creation of hair like structures.
Elliptic umbilic catastrophe

Arnold's notation
Vladimir ArnoldVladimir Arnold
Vladimir Igorevich Arnold was a Soviet and Russian mathematician. While he is best known for the Kolmogorov–Arnold–Moser theorem regarding the stability of integrable Hamiltonian systems, he made important contributions in several areas including dynamical systems theory, catastrophe theory,...
gave the catastrophes the ADE classification
ADE classification
In mathematics, the ADE classification is the complete list of simply laced Dynkin diagrams or other mathematical objects satisfying analogous axioms; "simply laced" means that there are no multiple edges, which corresponds to all simple roots in the root system forming angles of \pi/2 = 90^\circ ...
, due to a deep connection with simple Lie group
Simple Lie group
In group theory, a simple Lie group is a connected non-abelian Lie group G which does not have nontrivial connected normal subgroups.A simple Lie algebra is a non-abelian Lie algebra whose only ideals are 0 and itself...
s.
- A0 - a non-singular point:
 .
. - A1 - a local extremum, either a stable minimum or unstable maximum
 .
. - A2 - the fold
- A3 - the cusp
- A4 - the swallowtail
- A5 - the butterfly
- Ak - a representative of an infinite sequence of one variable forms

- D4- - the elliptical umbilic
- D4+ - the hyperbolic umbilic
- D5 - the parabolic umbilic
- Dk - a representative of an infinite sequence of further umbilic forms
- E6 - the symbolic umbilic

- E7
- E8
There are objects in singularity theory which correspond to most of the other simple Lie groups.
See also
- broken symmetry
- tipping pointTipping pointIn sociology, a tipping point is the event of a previously rare phenomenon becoming rapidly and dramatically more common. The phrase was coined in its sociological use by Morton Grodzins, by analogy with the fact in physics that adding a small amount of weight to a balanced object can cause it to...
- phase transitionPhase transitionA phase transition is the transformation of a thermodynamic system from one phase or state of matter to another.A phase of a thermodynamic system and the states of matter have uniform physical properties....
- domino effectDomino effectThe domino effect is a chain reaction that occurs when a small change causes a similar change nearby, which then will cause another similar change, and so on in linear sequence. The term is best known as a mechanical effect, and is used as an analogy to a falling row of dominoes...
- snowball effectSnowball effectSnowball effect is a figurative term for a process that starts from an initial state of small significance and builds upon itself, becoming larger , and perhaps potentially dangerous or disastrous , though it might be beneficial instead...
- butterfly effectButterfly effectIn chaos theory, the butterfly effect is the sensitive dependence on initial conditions; where a small change at one place in a nonlinear system can result in large differences to a later state...
- spontaneous symmetry breakingSpontaneous symmetry breakingSpontaneous symmetry breaking is the process by which a system described in a theoretically symmetrical way ends up in an apparently asymmetric state....
- chaos theoryChaos theoryChaos theory is a field of study in mathematics, with applications in several disciplines including physics, economics, biology, and philosophy. Chaos theory studies the behavior of dynamical systems that are highly sensitive to initial conditions, an effect which is popularly referred to as the...

