Dynamical system (definition)
Encyclopedia
The dynamical system concept is a mathematical
formalization
for any fixed "rule" which describes the time
dependence of a point's position in its ambient space
. The concept unifies very different types of such "rules" in mathematics: the different choices made for how time is measured and the special properties of the ambient space
may give an idea of the vastness of the class of objects described by this concept. Time can be measured by integers, by real or complex numbers or can be a more general algebraic object, losing the memory of its physical origin, and the ambient space may be simply a set, without the need of a smooth space-time structure defined on it.
and is measure theoretical in flavor. The measure theoretical definitions assume the existence of a measure-preserving transformation. This appears to exclude dissipative system
s, as in a dissipative system a small region of phase space shrinks under time evolution. A simple construction (sometimes called the Krylov-Bogolyubov theorem
) shows that it is always possible to construct a measure so as to make the evolution rule of the dynamical system a measure-preserving transformation. In the construction a given measure of the state space is summed for all future points of a trajectory, assuring the invariance.
The difficulty in constructing the natural measure for a dynamical system makes it difficult to develop ergodic theory starting from differential equations, so it becomes convenient to have a dynamical systems-motivated definition within ergodic theory that side-steps the choice of measure.
(T, M, Φ) where T is a monoid
, written additively, M is a set and Φ is a function
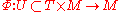
with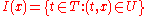
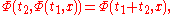for 
The function Φ(t,x) is called the evolution function of the dynamical system: it associates to every point in the set M a unique image, depending on the variable t, called the evolution parameter. M is called phase space
or state space, while the variable x represents an initial state of the system.
We often write
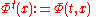
if we take one of the variables as constant.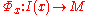
is called flow through x and its graph trajectory
through x. The set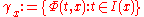
is called orbit
through x.
A subset S of the state space M is called Φ-invariant if for all x in S and all t in
In particular, for S to be Φ-invariant, we require that
for all 
in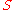 
. That is, the flow through x should be defined for all time for every element of 
.
).
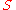is a tuple (T, M, Φ) with T an open interval in the real number
s R, M a manifold
locally diffeomorphic to a Banach space
, and Φ a continuous function
. If T=R we call the system global, if T is restricted to the non-negative reals we call the system a semi-flow. If Φ is continuously differentiable we say the system is a differentiable dynamical system. If the manifold M is locally diffeomorphic to Rn the dynamical system is finite-dimensional and if not, the dynamical system is infinite-dimensional.
(T, M, Φ) with T the integer
s, M a manifold
locally diffeomorphic to a Banach space
, and Φ a function. If T is restricted to the non-negative integers we call the system a semi-cascade.
such as the integer
s or a higher dimensional integer grid
, M a finite set, and Φ an evolution function. Some cellular automata are reversible dynamical systems, although most are not.
A dynamical system may be defined formally, as a measure-preserving transformation of a sigma-algebra
, the triplet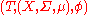
. Here, T is a monoid (usually the non-negative integers), X is a set, and Σ is a topology
on X, so that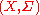
is a sigma-algebra. For every element 
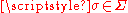, μ is its finite measure
, so that the triplet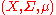
is a probability space. A map 
is said to be Σ-measurable
if and only if, for every
, one has 
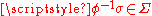. A map Φ is said to preserve the measure if and only if, for every 
, one has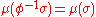 
. Combining the above, a map Φ is said to be a measure-preserving transformation of X , if it is a map from X to itself, it is Σ-measurable, and is measure-preserving. The triplet 
, for such a Φ, is then defined to be a dynamical system.
The map Φ embodies the time evolution of the dynamical system. Thus, for discrete dynamical systems the iterates
for every integer n are studied. For continuous dynamical systems, the map Φ is understood to be finite time evolution map and the construction is more complicated.
in Hamiltonian system
s, chosen over other invariant measures, such as the measures supported on periodic orbits of the Hamiltonian system. For many dissipative chaotic systems the choice of invariant measure is technically more challenging. The measure needs to be supported on the attractor
, but attractors have zero Lebesgue measure
and the invariant measures must be singular with respect to the Lebesgue measure.
For hyperbolic dynamical systems, the Sinai-Ruelle-Bowen measures appear to be the natural choice. They are constructed on the geometrical structure of stable and unstable manifolds of the dynamical system; they behave physically under small perturbations; and they explain many of the observed statistics of hyperbolic systems.
, that is the study of the initial value problem
s for their describing systems of ordinary differential equation
s.
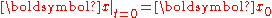
where
The solution is the evolution function already introduced in above
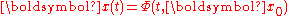
Some formal manipulation of the system of differential equation
s shown above gives a more general form of equations a dynamical system must satisfy
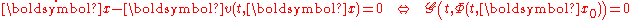
where
is a functional
from the set of evolution functions to the field of the complex numbers.
topological space
X, it is often useful to study the continuous extension Φ* of Φ to the one-point compactification X* of X. Although we lose the differential structure of the original system we can now use compactness arguments to analyze the new system (R, X*, Φ*).
In compact dynamical systems the limit set
of any orbit is non-empty, compact
and simply connected.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
formalization
Formalization
Formalization may refer to* formal system in formal logic* a process enhancing bureaucracy in sociology...
for any fixed "rule" which describes the time
Time
Time is a part of the measuring system used to sequence events, to compare the durations of events and the intervals between them, and to quantify rates of change such as the motions of objects....
dependence of a point's position in its ambient space
Space
Space is the boundless, three-dimensional extent in which objects and events occur and have relative position and direction. Physical space is often conceived in three linear dimensions, although modern physicists usually consider it, with time, to be part of a boundless four-dimensional continuum...
. The concept unifies very different types of such "rules" in mathematics: the different choices made for how time is measured and the special properties of the ambient space
Ambient space
An ambient space, ambient configuration space, or electroambient space, is the space surrounding an object.-Mathematics:In mathematics, especially in geometry and topology, an ambient space is the space surrounding a mathematical object...
may give an idea of the vastness of the class of objects described by this concept. Time can be measured by integers, by real or complex numbers or can be a more general algebraic object, losing the memory of its physical origin, and the ambient space may be simply a set, without the need of a smooth space-time structure defined on it.
Formal definition
There are two classes of definitions for a dynamical system: one is motivated by ordinary differential equations and is geometrical in flavor; and the other is motivated by ergodic theoryErgodic theory
Ergodic theory is a branch of mathematics that studies dynamical systems with an invariant measure and related problems. Its initial development was motivated by problems of statistical physics....
and is measure theoretical in flavor. The measure theoretical definitions assume the existence of a measure-preserving transformation. This appears to exclude dissipative system
Dissipative system
A dissipative system is a thermodynamically open system which is operating out of, and often far from, thermodynamic equilibrium in an environment with which it exchanges energy and matter....
s, as in a dissipative system a small region of phase space shrinks under time evolution. A simple construction (sometimes called the Krylov-Bogolyubov theorem
Krylov-Bogolyubov theorem
In mathematics, the Krylov–Bogolyubov theorem may refer to any of the two related fundamental theorems within the theory of dynamical systems...
) shows that it is always possible to construct a measure so as to make the evolution rule of the dynamical system a measure-preserving transformation. In the construction a given measure of the state space is summed for all future points of a trajectory, assuring the invariance.
The difficulty in constructing the natural measure for a dynamical system makes it difficult to develop ergodic theory starting from differential equations, so it becomes convenient to have a dynamical systems-motivated definition within ergodic theory that side-steps the choice of measure.
General definition
In the most general sense, a dynamical system is a tupleTuple
In mathematics and computer science, a tuple is an ordered list of elements. In set theory, an n-tuple is a sequence of n elements, where n is a positive integer. There is also one 0-tuple, an empty sequence. An n-tuple is defined inductively using the construction of an ordered pair...
(T, M, Φ) where T is a monoid
Monoid
In abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
, written additively, M is a set and Φ is a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
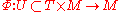
with
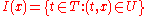
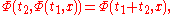for The function Φ(t,x) is called the evolution function of the dynamical system: it associates to every point in the set M a unique image, depending on the variable t, called the evolution parameter. M is called phase space
Phase space
In mathematics and physics, a phase space, introduced by Willard Gibbs in 1901, is a space in which all possible states of a system are represented, with each possible state of the system corresponding to one unique point in the phase space...
or state space, while the variable x represents an initial state of the system.
We often write
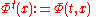
if we take one of the variables as constant.
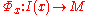
is called flow through x and its graph trajectory
Trajectory
A trajectory is the path that a moving object follows through space as a function of time. The object might be a projectile or a satellite, for example. It thus includes the meaning of orbit—the path of a planet, an asteroid or a comet as it travels around a central mass...
through x. The set
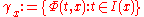
is called orbit
Orbit (dynamics)
In mathematics, in the study of dynamical systems, an orbit is a collection of points related by the evolution function of the dynamical system. The orbit is a subset of the phase space and the set of all orbits is a partition of the phase space, that is different orbits do not intersect in the...
through x.
A subset S of the state space M is called Φ-invariant if for all x in S and all t in
In particular, for S to be Φ-invariant, we require that
for all in 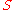. That is, the flow through x should be defined for all time for every element of 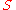.Geometrical cases
In these cases M is a manifold (or its extreme case a graphGraph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
).
Real dynamical system
A real dynamical system, real-time dynamical system or flowFlow (mathematics)
In mathematics, a flow formalizes the idea of the motion of particles in a fluid. Flows are ubiquitous in science, including engineering and physics. The notion of flow is basic to the study of ordinary differential equations. Informally, a flow may be viewed as a continuous motion of points over...
is a tuple (T, M, Φ) with T an open interval in the real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s R, M a manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
locally diffeomorphic to a Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
, and Φ a continuous function
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
. If T=R we call the system global, if T is restricted to the non-negative reals we call the system a semi-flow. If Φ is continuously differentiable we say the system is a differentiable dynamical system. If the manifold M is locally diffeomorphic to Rn the dynamical system is finite-dimensional and if not, the dynamical system is infinite-dimensional.
Discrete dynamical system
A discrete dynamical system, discrete-time dynamical system, map or cascade is a tupleTuple
In mathematics and computer science, a tuple is an ordered list of elements. In set theory, an n-tuple is a sequence of n elements, where n is a positive integer. There is also one 0-tuple, an empty sequence. An n-tuple is defined inductively using the construction of an ordered pair...
(T, M, Φ) with T the integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s, M a manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
locally diffeomorphic to a Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
, and Φ a function. If T is restricted to the non-negative integers we call the system a semi-cascade.
Cellular automaton
A cellular automaton is a tuple (T, M, Φ), with T a latticeLattice (group)
In mathematics, especially in geometry and group theory, a lattice in Rn is a discrete subgroup of Rn which spans the real vector space Rn. Every lattice in Rn can be generated from a basis for the vector space by forming all linear combinations with integer coefficients...
such as the integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s or a higher dimensional integer grid
Integer lattice
In mathematics, the n-dimensional integer lattice , denoted Zn, is the lattice in the Euclidean space Rn whose lattice points are n-tuples of integers. The two-dimensional integer lattice is also called the square lattice, or grid lattice. Zn is the simplest example of a root lattice...
, M a finite set, and Φ an evolution function. Some cellular automata are reversible dynamical systems, although most are not.
Measure theoretical definition
- See main article measure-preserving dynamical systemMeasure-preserving dynamical systemIn mathematics, a measure-preserving dynamical system is an object of study in the abstract formulation of dynamical systems, and ergodic theory in particular.-Definition:...
.
A dynamical system may be defined formally, as a measure-preserving transformation of a sigma-algebra
Sigma-algebra
In mathematics, a σ-algebra is a technical concept for a collection of sets satisfying certain properties. The main use of σ-algebras is in the definition of measures; specifically, the collection of sets over which a measure is defined is a σ-algebra...
, the triplet
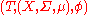. Here, T is a monoid (usually the non-negative integers), X is a set, and Σ is a topologyTopology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
on X, so that
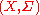is a sigma-algebra. For every element 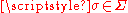, μ is its finite measureMeasure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
, so that the triplet
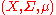is a probability space. A map is said to be Σ-measurableMeasurable function
In mathematics, particularly in measure theory, measurable functions are structure-preserving functions between measurable spaces; as such, they form a natural context for the theory of integration...
if and only if, for every
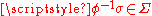, one has . A map Φ is said to preserve the measure if and only if, for every , one has 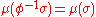. Combining the above, a map Φ is said to be a measure-preserving transformation of X , if it is a map from X to itself, it is Σ-measurable, and is measure-preserving. The triplet , for such a Φ, is then defined to be a dynamical system.The map Φ embodies the time evolution of the dynamical system. Thus, for discrete dynamical systems the iterates
Iterated function
In mathematics, an iterated function is a function which is composed with itself, possibly ad infinitum, in a process called iteration. In this process, starting from some initial value, the result of applying a given function is fed again in the function as input, and this process is repeated...
for every integer n are studied. For continuous dynamical systems, the map Φ is understood to be finite time evolution map and the construction is more complicated.Relation to geometric definition
Many different invariant measures can be associated to any one evolution rule. In ergodic theory the choice is assumed made, but if the dynamical system is given by a system of differential equations the appropriate measure must be determined. Some systems have a natural measure, such as the Liouville measureLiouville's theorem (Hamiltonian)
In physics, Liouville's theorem, named after the French mathematician Joseph Liouville, is a key theorem in classical statistical and Hamiltonian mechanics...
in Hamiltonian system
Hamiltonian system
In physics and classical mechanics, a Hamiltonian system is a physical system in which forces are momentum invariant. Hamiltonian systems are studied in Hamiltonian mechanics....
s, chosen over other invariant measures, such as the measures supported on periodic orbits of the Hamiltonian system. For many dissipative chaotic systems the choice of invariant measure is technically more challenging. The measure needs to be supported on the attractor
Attractor
An attractor is a set towards which a dynamical system evolves over time. That is, points that get close enough to the attractor remain close even if slightly disturbed...
, but attractors have zero Lebesgue measure
Lebesgue measure
In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
and the invariant measures must be singular with respect to the Lebesgue measure.
For hyperbolic dynamical systems, the Sinai-Ruelle-Bowen measures appear to be the natural choice. They are constructed on the geometrical structure of stable and unstable manifolds of the dynamical system; they behave physically under small perturbations; and they explain many of the observed statistics of hyperbolic systems.
Construction of dynamical systems
The concept of evolution in time is central to the theory of dynamical systems as seen in the previous sections: the basic reason for this fact is that the starting motivation of the theory was the study of time behavior of classical mechanical systemsClassical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
, that is the study of the initial value problem
Initial value problem
In mathematics, in the field of differential equations, an initial value problem is an ordinary differential equation together with a specified value, called the initial condition, of the unknown function at a given point in the domain of the solution...
s for their describing systems of ordinary differential equation
Ordinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
s.
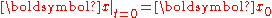
where
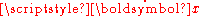represents the velocityVelocityIn physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...
of the material point
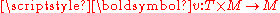is a vector fieldVector fieldIn vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
in
or 
and represents the change of velocityVelocityIn physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...
induced by the known forceForceIn physics, a force is any influence that causes an object to undergo a change in speed, a change in direction, or a change in shape. In other words, a force is that which can cause an object with mass to change its velocity , i.e., to accelerate, or which can cause a flexible object to deform...
s acting on the given material point. Depending on the properties of this vector field, the mechanical system is called- autonomous, when
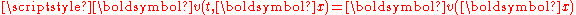
- homogeneous when
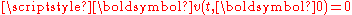for all 
The solution is the evolution function already introduced in above
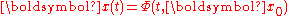
Some formal manipulation of the system of differential equation
Differential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
s shown above gives a more general form of equations a dynamical system must satisfy
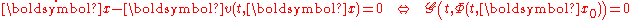
where
is a functionalFunctional
Generally, functional refers to something able to fulfill its purpose or function.*Functionalism and Functional form, movements in architectural design*Functional group, certain atomic combinations that occur in various molecules, e.g...
from the set of evolution functions to the field of the complex numbers.
Compactification of a dynamical system
Given a global dynamical system (R, X, Φ) on a locally compact and HausdorffHausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
X, it is often useful to study the continuous extension Φ* of Φ to the one-point compactification X* of X. Although we lose the differential structure of the original system we can now use compactness arguments to analyze the new system (R, X*, Φ*).
In compact dynamical systems the limit set
Limit set
In mathematics, especially in the study of dynamical systems, a limit set is the state a dynamical system reaches after an infinite amount of time has passed, by either going forward or backwards in time...
of any orbit is non-empty, compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
and simply connected.