
Krylov-Bogolyubov theorem
Encyclopedia
In mathematics
, the Krylov–Bogolyubov theorem (also known as the existence of invariant measures theorem) may refer to any of the two related fundamental theorem
s within the theory of dynamical systems. The theorems guarantee the existence of invariant measure
s for certain "nice" maps defined on "nice" spaces and were named after Russia
n-Ukrainian
mathematician
s and theoretical physicists
Nikolay Krylov
and Nikolay Bogolyubov
who proved the theorems.
, metrizable
topological space
and F : X → X a continuous map. Then F admits an invariant Borel probability measure
.
That is, if Borel(X) denotes the Borel σ-algebra generated by the collection T of open subsets
of X, then there exists a probability measure μ : Borel(X) → [0, 1] such that for any subset A ∈ Borel(X),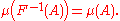
In terms of the push forward
, this states that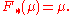
and let be the transition probabilities for a time-homogeneous Markov
be the transition probabilities for a time-homogeneous Markov
semigroup
on X, i.e.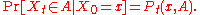
Theorem (Krylov–Bogolyubov): If there exists a point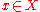 for which the family of probability measures { Pt(x, ·) | t > 0 } is uniformly tight
for which the family of probability measures { Pt(x, ·) | t > 0 } is uniformly tight
and the semigroup (Pt) satisfies the Feller property
, then there exists at least one invariant measure for (Pt), i.e. a probability measure μ on X such that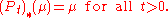
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Krylov–Bogolyubov theorem (also known as the existence of invariant measures theorem) may refer to any of the two related fundamental theorem
Theorem
In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...
s within the theory of dynamical systems. The theorems guarantee the existence of invariant measure
Invariant measure
In mathematics, an invariant measure is a measure that is preserved by some function. Ergodic theory is the study of invariant measures in dynamical systems...
s for certain "nice" maps defined on "nice" spaces and were named after Russia
Russia
Russia or , officially known as both Russia and the Russian Federation , is a country in northern Eurasia. It is a federal semi-presidential republic, comprising 83 federal subjects...
n-Ukrainian
Ukraine
Ukraine is a country in Eastern Europe. It has an area of 603,628 km², making it the second largest contiguous country on the European continent, after Russia...
mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
s and theoretical physicists
Theoretical physics
Theoretical physics is a branch of physics which employs mathematical models and abstractions of physics to rationalize, explain and predict natural phenomena...
Nikolay Krylov
Nikolay Mitrofanovich Krylov
Nikolay Mitrofanovich Krylov was a Russian and Soviet mathematician known for works on interpolation, non-linear mechanics, and numerical methods for solving equations of mathematical physics.-Biography:...
and Nikolay Bogolyubov
Nikolay Bogolyubov
Nikolay Nikolaevich Bogolyubov was a Russian and Ukrainian Soviet mathematician and theoretical physicist known for a significant contribution to quantum field theory, classical and quantum statistical mechanics, and to the theory of dynamical systems; a recipient of the Dirac Prize...
who proved the theorems.
Invariant measures for a single map
Theorem (Krylov–Bogolyubov): Let (X, T) be a compactCompact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
, metrizable
Metrization theorem
In topology and related areas of mathematics, a metrizable space is a topological space that is homeomorphic to a metric space. That is, a topological space is said to be metrizable if there is a metricd\colon X \times X \to [0,\infty)...
topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
and F : X → X a continuous map. Then F admits an invariant Borel probability measure
Probability measure
In mathematics, a probability measure is a real-valued function defined on a set of events in a probability space that satisfies measure properties such as countable additivity...
.
That is, if Borel(X) denotes the Borel σ-algebra generated by the collection T of open subsets
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
of X, then there exists a probability measure μ : Borel(X) → [0, 1] such that for any subset A ∈ Borel(X),
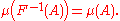
In terms of the push forward
Pushforward measure
In measure theory, a pushforward measure is obtained by transferring a measure from one measurable space to another using a measurable function.-Definition:...
, this states that
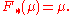
Invariant measures for a Markov process
Let X be a Polish spacePolish space
In the mathematical discipline of general topology, a Polish space is a separable completely metrizable topological space; that is, a space homeomorphic to a complete metric space that has a countable dense subset. Polish spaces are so named because they were first extensively studied by Polish...
and let
 be the transition probabilities for a time-homogeneous Markov
be the transition probabilities for a time-homogeneous MarkovMarkov process
In probability theory and statistics, a Markov process, named after the Russian mathematician Andrey Markov, is a time-varying random phenomenon for which a specific property holds...
semigroup
Semigroup
In mathematics, a semigroup is an algebraic structure consisting of a set together with an associative binary operation. A semigroup generalizes a monoid in that there might not exist an identity element...
on X, i.e.
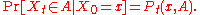
Theorem (Krylov–Bogolyubov): If there exists a point
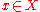 for which the family of probability measures { Pt(x, ·) | t > 0 } is uniformly tight
for which the family of probability measures { Pt(x, ·) | t > 0 } is uniformly tightTightness of measures
In mathematics, tightness is a concept in measure theory. The intuitive idea is that a given collection of measures does not "escape to infinity."-Definitions:...
and the semigroup (Pt) satisfies the Feller property
Feller-continuous process
In mathematics, a Feller-continuous process is a continuous-time stochastic process for which the expected value of suitable statistics of the process at a given time in the future depend continuously on the initial condition of the process...
, then there exists at least one invariant measure for (Pt), i.e. a probability measure μ on X such that
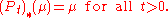
See also
- For the 1st theorem: Ya. G. Sinai (Ed.) (1997): Dynamical Systems II. Ergodic Theory with Applications to Dynamical Systems and Statistical Mechanics. Berlin, New York: Springer-Verlag. ISBN 3-540-17001-4. (Section 1).
- For the 2nd theorem: G. Da Prato and J. Zabczyk (1996): Ergodicity for Infinite Dimensional Systems. Cambridge Univ. Press. ISBN 0-521-57900-7. (Section 3).

