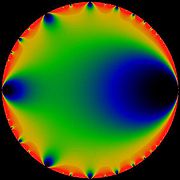
For other meanings, see List of topics named after Leonhard Euler.

In mathematics

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, the Euler function is given by
Named after Leonhard Euler

Leonhard Euler

Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...

, it is a prototypical example of a q-series, a modular form

Modular form

In mathematics, a modular form is a analytic function on the upper half-plane satisfying a certain kind of functional equation and growth condition. The theory of modular forms therefore belongs to complex analysis but the main importance of the theory has traditionally been in its connections...

, and provides the prototypical example of a relation between combinatorics

Combinatorics

Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...

 and complex analysis

Complex analysis

Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...

.

Properties

The coefficient

Coefficient

In mathematics, a coefficient is a multiplicative factor in some term of an expression ; it is usually a number, but in any case does not involve any variables of the expression...

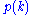  in the formal power series

Formal power series

In mathematics, formal power series are a generalization of polynomials as formal objects, where the number of terms is allowed to be infinite; this implies giving up the possibility to substitute arbitrary values for indeterminates...

 expansion for 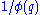gives the number of all partitions of k. That is,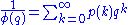
where 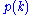is the partition function of k.

The Euler identity, also known as the Pentagonal number theorem is

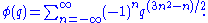
Note that 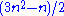is a pentagonal number

Pentagonal number

A pentagonal number is a figurate number that extends the concept of triangular and square numbers to the pentagon, but, unlike the first two, the patterns involved in the construction of pentagonal numbers are not rotationally symmetrical...

.

The Euler function is related to the Dedekind eta function

Dedekind eta function

The Dedekind eta function, named after Richard Dedekind, is a function defined on the upper half-plane of complex numbers, where the imaginary part is positive...

 through a Ramanujan identity as

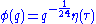
where 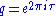is the square of the nome.

Note that both functions have the symmetry of the modular group

Modular group

In mathematics, the modular group Γ is a fundamental object of study in number theory, geometry, algebra, and many other areas of advanced mathematics...

.

The Euler function may be expressed as a Q-Pochhammer symbol:


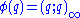
The logarithm of the Euler function is the sum of the logarithms in the product expression, each of which may be expanded about q=1, yielding:


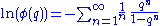
which is a Lambert series with coefficients -1/n. The logarithm of the Euler function may therefore be expressed as:


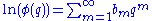
where
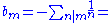-[1/1, 3/2, 4/3, 7/4, 6/5, 12/6, 8/7, 15/8, 13/9, 18/10, ...] (see OEIS A000203)