A pentagonal number is a figurate number

Figurate number

The term figurate number is used by different writers for members of different sets of numbers, generalizing from triangular numbers to different shapes and different dimensions...

 that extends the concept of triangular

Triangular number

A triangular number or triangle number numbers the objects that can form an equilateral triangle, as in the diagram on the right. The nth triangle number is the number of dots in a triangle with n dots on a side; it is the sum of the n natural numbers from 1 to n...

 and square number

Square number

In mathematics, a square number, sometimes also called a perfect square, is an integer that is the square of an integer; in other words, it is the product of some integer with itself...

s to the pentagon

Pentagon

In geometry, a pentagon is any five-sided polygon. A pentagon may be simple or self-intersecting. The sum of the internal angles in a simple pentagon is 540°. A pentagram is an example of a self-intersecting pentagon.- Regular pentagons :In a regular pentagon, all sides are equal in length and...

, but, unlike the first two, the patterns involved in the construction of pentagonal numbers are not rotationally symmetrical

Rotational symmetry

Generally speaking, an object with rotational symmetry is an object that looks the same after a certain amount of rotation. An object may have more than one rotational symmetry; for instance, if reflections or turning it over are not counted, the triskelion appearing on the Isle of Man's flag has...

. The nth pentagonal number p_n is the number of distinct dots in a pattern of dots consisting of the outlines of regular pentagons whose sides contain 1 to n dots, overlaid so that they share one vertex

Vertex (geometry)

In geometry, a vertex is a special kind of point that describes the corners or intersections of geometric shapes.-Of an angle:...

. For instance, the third one is formed from outlines comprising 1, 5 and 10 dots, but the 1, and 3 of the 5, coincide with 3 of the 10 – leaving 12 distinct dots, 10 in the form of a pentagon, and 2 inside.

p_n is given by the formula:


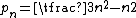
for n ≥ 1. The first few pentagonal numbers are:

1, 5, 12

12 (number)

12 is the natural number following 11 and preceding 13.The word "twelve" is the largest number with a single-morpheme name in English. Etymology suggests that "twelve" arises from the Germanic compound twalif "two-leftover", so a literal translation would yield "two remaining [after having ten...

, 22

22 (number)

22 is the natural number following 21 and preceding 23.- In mathematics :Twenty-two is an even composite number, its proper divisors being 1, 2 and 11....

, 35

35 (number)

35 is the natural number following 34 and preceding 36.- In mathematics :35 is the sum of the first five triangular numbers, making it a tetrahedral number....

, 51, 70

70 (number)

70 is the natural number following 69 and preceding 71.-In mathematics:Its factorization makes it a sphenic number. 70 is a Pell number and a generalized heptagonal number, one of only two numbers to be both. Also, it is the seventh pentagonal number and the fourth 13-gonal number, as well as the...

, 92

92 (number)

92 is the natural number following 91 and preceding 93.- In mathematics:Ninety-two is a pentagonal number.There are 92 Johnson solids...

, 117

117 (number)

117 is the natural number following 116 and preceding 118.-In mathematics:One hundred seventeen is the smallest possible length of the longest side of a Heronian tetrahedron .117 is a pentagonal number.In base 10, it is a Harshad number.-In other fields:One hundred seventeen is also:* The...

, 145, 176, 210, 247, 287, 330, 376, 425, 477, 532, 590, 651, 715, 782, 852, 925, 1001

1001 (number)

1001 is the natural number following 1000 and followed by 1002.- In mathematics :One thousand and one is a sphenic number, a pentagonal number, a pentatope number and the first four-digit palindromic number.- In other fields :...

 .

The nth pentagonal number is one third of the 3n-1th triangular number

Triangular number

A triangular number or triangle number numbers the objects that can form an equilateral triangle, as in the diagram on the right. The nth triangle number is the number of dots in a triangle with n dots on a side; it is the sum of the n natural numbers from 1 to n...

.

Generalized pentagonal numbers are obtained from the formula given above, but with n taking values in the sequence 0, 1, -1, 2, -2, 3, -3, 4..., producing the sequence:

0, 1, 2, 5, 7, 12, 15, 22, 26, 35, 40, 51, 57, 70, 77, 92, 100, 117, 126, 145, 155, 176, 187, 210, 222, 247, 260, 287, 301, 330, 345, 376, 392, 425, 442, 477, 495, 532, 551, 590, 610, 651, 672, 715, 737, 782, 805, 852, 876, 925, 950, 1001, 1027, 1080, 1107, 1162, 1190, 1247, 1276, 1335... .

Generalized pentagonal numbers are important to Euler's theory of partition

Partition (number theory)

In number theory and combinatorics, a partition of a positive integer n, also called an integer partition, is a way of writing n as a sum of positive integers. Two sums that differ only in the order of their summands are considered to be the same partition; if order matters then the sum becomes a...

s, as expressed in his pentagonal number theorem.

The number of dots inside the outermost pentagon of a pattern forming a pentagonal number is itself a generalized pentagonal number.

Pentagonal numbers should not be confused with centered pentagonal number

Centered pentagonal number

A centered pentagonal number is a centered figurate number that represents a pentagon with a dot in the center and all other dots surrounding the center in successive pentagonal layers...

s.

Generalized pentagonal numbers and centered hexagonal numbers

Generalized pentagonal numbers are closely related to centered hexagonal number

Centered hexagonal number

A centered hexagonal number, or hex number, is a centered figurate number that represents a hexagon with a dot in the center and all other dots surrounding the center dot in a hexagonal lattice....

s. When the array corresponding to a centered hexagonal number is divided between its middle row and an adjacent row, it appears as the sum of two generalized pentagonal numbers, with the larger piece being a pentagonal number proper:

1=1+0		7=5+2		19=12+7		37=22+15
		> >		> > > >		> > > > > >

In general:


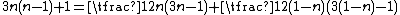
where both terms on the right are generalized pentagonal numbers and the first term is a pentagonal number proper (n ≥ 1). This division of centered hexagonal arrays gives generalized pentagonal numbers as trapezoidal arrays, which may be interpreted as Ferrers diagrams for their partition. In this way they can be used to prove the pentagonal number theorem referenced above.

Tests for pentagonal numbers

One can test whether a positive integer x is a (non-generalized) pentagonal number by computing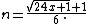


If n is a natural number

Natural number

In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...

, then x is the nth pentagonal number. If n is not a natural number, then x is not pentagonal.