
Figurate number
Encyclopedia
The term figurate number is used by different writers for members of different sets of numbers, generalizing from triangular numbers to different shapes (polygonal numbers) and different dimensions (polyhedral numbers). The term can mean
In historical works about Greek mathematics
the preferred term used to be figured number.
In a use going back to Jakob Bernoulli's Ars Conjectandi
, the term figurate number is used for triangular numbers made up of successive integers, tetrahedral number
s made up of successive triangular numbers, etc. These turn out to be the binomial coefficients. In this usage the square numbers 4, 9, 16, 25 would not be considered figurate numbers when viewed as arranged in a square.
A number of other sources use the term figurate number as synonymous for the polygonal number
s, either just the usual kind or both those and the centered polygonal numbers.
, possibly based on Babylonian or Egyptian precursors. Generating whichever class of figurate numbers the Pythagoreans studied using gnomons
is also attributed to Pythagoras. Unfortunately, there is no trustworthy source for these claims, because all surviving writings about the Pythagoreans are from centuries later. It seems to be certain that the fourth triangular number of ten objects, called tetractys
in Greek, was a central part of the Pythagorean religion
, along with several other figures also called tetratcys. Figurate numbers were a concern of Pythagorean geometry.
The modern study of figurate numbers goes back to Fermat, specifically the Fermat polygonal number theorem
. Later, it became a significant topic for Euler, who gave an explicit formula for all triangular numbers that are also perfect squares
, among many other discoveries relating to figurate numbers.
Figurate numbers have played a significant role in modern recreational mathematics. In research mathematics, figurate numbers are studied by way of the Ehrhart polynomial
s, polynomial
s that count the number of integer points in a polygon or polyhedron when it is expanded by a given factor.
s for n = 1, 2, 3, ... are the result of the juxtaposition of the linear numbers (linear gnomon
s) for n = 1, 2, 3, ...:
These are the binomial coefficients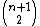 . This is the case r=2 of the fact that the rth diagonal of Pascal's triangle for
. This is the case r=2 of the fact that the rth diagonal of Pascal's triangle for 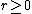 consists of the figurate numbers for the r-dimensional analogs of triangles (r-dimensional simplices
consists of the figurate numbers for the r-dimensional analogs of triangles (r-dimensional simplices
).
The simplicial polytopic numbers for r = 1, 2, 3, 4, ... are:

The terms square number
and cubic number derive from their geometric representation as a square
or cube. The difference of two positive triangular numbers is a trapezoidal number.
For example, the gnomon of the square number is the odd number, of the general form 2n + 1, n = 0, 1, 2, 3, ... . The square of size 8 composed of gnomons looks like this:
8 8 8 8 8 8 8 8
8 7 7 7 7 7 7 7
8 7 6 6 6 6 6 6
8 7 6 5 5 5 5 5
8 7 6 5 4 4 4 4
8 7 6 5 4 3 3 3
8 7 6 5 4 3 2 2
8 7 6 5 4 3 2 1
To transform from the n-square (the square of size n) to the (n + 1)-square, one adjoins 2n + 1 elements: one to the end of each row (n elements), one to the end of each column (n elements), and a single one to the corner. For example, when transforming the 7-square to the 8-square, we add 15 elements; these adjunctions are the 8s in the above figure.
This gnomonic technique also provides a mathematical proof
that the sum of the first n odd numbers is n2; the figure illustrates 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 = 64 = 82.
- polygonal number
- a number represented as a discrete r-dimensional regular geometricGeometryGeometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
pattern of r-dimensional ballsBall (mathematics)In mathematics, a ball is the space inside a sphere. It may be a closed ball or an open ball ....
such as a polygonal numberPolygonal numberIn mathematics, a polygonal number is a number represented as dots or pebbles arranged in the shape of a regular polygon. The dots were thought of as alphas . These are one type of 2-dimensional figurate numbers.- Definition and examples :...
(for r = 2) or a polyhedral number (for r = 3).
- a member of the subset of the sets above containing only triangular numbers, pyramidal numbers, and their analogs in other dimensions.
Terminology
Some kinds of figurate number were discussed in the 16th and 17th centuries under the name "figural number".In historical works about Greek mathematics
Greek mathematics
Greek mathematics, as that term is used in this article, is the mathematics written in Greek, developed from the 7th century BC to the 4th century AD around the Eastern shores of the Mediterranean. Greek mathematicians lived in cities spread over the entire Eastern Mediterranean, from Italy to...
the preferred term used to be figured number.
In a use going back to Jakob Bernoulli's Ars Conjectandi
Ars Conjectandi
Ars Conjectandi is a combinatorial mathematical paper written by Jakob Bernoulli and published in 1713, eight years after his death, by his nephew, Niklaus Bernoulli. The seminal work consolidated, most notably among other combinatorial topics, probability theory: indeed, it is widely regarded as...
, the term figurate number is used for triangular numbers made up of successive integers, tetrahedral number
Tetrahedral number
A tetrahedral number, or triangular pyramidal number, is a figurate number that represents a pyramid with a triangular base and three sides, called a tetrahedron...
s made up of successive triangular numbers, etc. These turn out to be the binomial coefficients. In this usage the square numbers 4, 9, 16, 25 would not be considered figurate numbers when viewed as arranged in a square.
A number of other sources use the term figurate number as synonymous for the polygonal number
Polygonal number
In mathematics, a polygonal number is a number represented as dots or pebbles arranged in the shape of a regular polygon. The dots were thought of as alphas . These are one type of 2-dimensional figurate numbers.- Definition and examples :...
s, either just the usual kind or both those and the centered polygonal numbers.
History
The mathematical study of figurate numbers is said to have originated with PythagorasPythagoras
Pythagoras of Samos was an Ionian Greek philosopher, mathematician, and founder of the religious movement called Pythagoreanism. Most of the information about Pythagoras was written down centuries after he lived, so very little reliable information is known about him...
, possibly based on Babylonian or Egyptian precursors. Generating whichever class of figurate numbers the Pythagoreans studied using gnomons
Gnomon (figure)
In geometry, a gnomon is a plane figure formed by removing a similar parallelogram from a corner of a larger parallelogram. More generically, the term gnomon denotes the form that is to be added to a figure to produce a larger figure of the same shape....
is also attributed to Pythagoras. Unfortunately, there is no trustworthy source for these claims, because all surviving writings about the Pythagoreans are from centuries later. It seems to be certain that the fourth triangular number of ten objects, called tetractys
Tetractys
The tetractys , or tetrad, is a triangular figure consisting of ten points arranged in four rows: one, two, three, and four points in each row...
in Greek, was a central part of the Pythagorean religion
Pythagoreanism
Pythagoreanism was the system of esoteric and metaphysical beliefs held by Pythagoras and his followers, the Pythagoreans, who were considerably influenced by mathematics. Pythagoreanism originated in the 5th century BCE and greatly influenced Platonism...
, along with several other figures also called tetratcys. Figurate numbers were a concern of Pythagorean geometry.
The modern study of figurate numbers goes back to Fermat, specifically the Fermat polygonal number theorem
Fermat polygonal number theorem
In additive number theory, the Fermat polygonal number theorem states that every positive integer is a sum of at most -gonal numbers. That is, every positive number can be written as the sum of three or fewer triangular numbers, and as the sum of four or fewer square numbers, and as the sum of...
. Later, it became a significant topic for Euler, who gave an explicit formula for all triangular numbers that are also perfect squares
Square triangular number
In mathematics, a square triangular number is a number which is both a triangular number and a perfect square....
, among many other discoveries relating to figurate numbers.
Figurate numbers have played a significant role in modern recreational mathematics. In research mathematics, figurate numbers are studied by way of the Ehrhart polynomial
Ehrhart polynomial
In mathematics, an integral polytope has an associated Ehrhart polynomial which encodes the relationship between the volume of a polytope and the number of integer points the polytope contains...
s, polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
s that count the number of integer points in a polygon or polyhedron when it is expanded by a given factor.
Triangular numbers
The triangular numberTriangular number
A triangular number or triangle number numbers the objects that can form an equilateral triangle, as in the diagram on the right. The nth triangle number is the number of dots in a triangle with n dots on a side; it is the sum of the n natural numbers from 1 to n...
s for n = 1, 2, 3, ... are the result of the juxtaposition of the linear numbers (linear gnomon
Gnomon
The gnomon is the part of a sundial that casts the shadow. Gnomon is an ancient Greek word meaning "indicator", "one who discerns," or "that which reveals."It has come to be used for a variety of purposes in mathematics and other fields....
s) for n = 1, 2, 3, ...:
 |
   |
      |
          |
               |
                     |
These are the binomial coefficients
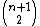 . This is the case r=2 of the fact that the rth diagonal of Pascal's triangle for
. This is the case r=2 of the fact that the rth diagonal of Pascal's triangle for 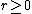 consists of the figurate numbers for the r-dimensional analogs of triangles (r-dimensional simplices
consists of the figurate numbers for the r-dimensional analogs of triangles (r-dimensional simplicesSimplex
In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...
).
The simplicial polytopic numbers for r = 1, 2, 3, 4, ... are:
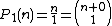 (linear numbers),
(linear numbers),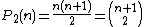 (triangular numberTriangular numberA triangular number or triangle number numbers the objects that can form an equilateral triangle, as in the diagram on the right. The nth triangle number is the number of dots in a triangle with n dots on a side; it is the sum of the n natural numbers from 1 to n...
(triangular numberTriangular numberA triangular number or triangle number numbers the objects that can form an equilateral triangle, as in the diagram on the right. The nth triangle number is the number of dots in a triangle with n dots on a side; it is the sum of the n natural numbers from 1 to n...
s), (tetrahedral numberTetrahedral numberA tetrahedral number, or triangular pyramidal number, is a figurate number that represents a pyramid with a triangular base and three sides, called a tetrahedron...
(tetrahedral numberTetrahedral numberA tetrahedral number, or triangular pyramidal number, is a figurate number that represents a pyramid with a triangular base and three sides, called a tetrahedron...
s),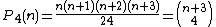 (pentachoron numbers, pentatopic numbers, 4-simplex numbers),
(pentachoron numbers, pentatopic numbers, 4-simplex numbers),

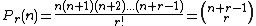 (r-topic numbers, r-simplexSimplexIn geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...
(r-topic numbers, r-simplexSimplexIn geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...
numbers).
The terms square number
Square number
In mathematics, a square number, sometimes also called a perfect square, is an integer that is the square of an integer; in other words, it is the product of some integer with itself...
and cubic number derive from their geometric representation as a square
Square (geometry)
In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles...
or cube. The difference of two positive triangular numbers is a trapezoidal number.
Gnomon
The gnomon is the piece added to a figurate number to transform it to the next larger one.For example, the gnomon of the square number is the odd number, of the general form 2n + 1, n = 0, 1, 2, 3, ... . The square of size 8 composed of gnomons looks like this:
8 8 8 8 8 8 8 8
8 7 7 7 7 7 7 7
8 7 6 6 6 6 6 6
8 7 6 5 5 5 5 5
8 7 6 5 4 4 4 4
8 7 6 5 4 3 3 3
8 7 6 5 4 3 2 2
8 7 6 5 4 3 2 1
To transform from the n-square (the square of size n) to the (n + 1)-square, one adjoins 2n + 1 elements: one to the end of each row (n elements), one to the end of each column (n elements), and a single one to the corner. For example, when transforming the 7-square to the 8-square, we add 15 elements; these adjunctions are the 8s in the above figure.
This gnomonic technique also provides a mathematical proof
Mathematical proof
In mathematics, a proof is a convincing demonstration that some mathematical statement is necessarily true. Proofs are obtained from deductive reasoning, rather than from inductive or empirical arguments. That is, a proof must demonstrate that a statement is true in all cases, without a single...
that the sum of the first n odd numbers is n2; the figure illustrates 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 = 64 = 82.

