
Tetrahedral number
Encyclopedia

Figurate number
The term figurate number is used by different writers for members of different sets of numbers, generalizing from triangular numbers to different shapes and different dimensions...
that represents a pyramid
Pyramid (geometry)
In geometry, a pyramid is a polyhedron formed by connecting a polygonal base and a point, called the apex. Each base edge and apex form a triangle. It is a conic solid with polygonal base....
with a triangular base and three sides, called a tetrahedron
Tetrahedron
In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...
. The nth tetrahedral number is the sum of the first n triangular number
Triangular number
A triangular number or triangle number numbers the objects that can form an equilateral triangle, as in the diagram on the right. The nth triangle number is the number of dots in a triangle with n dots on a side; it is the sum of the n natural numbers from 1 to n...
s.
The first few tetrahedral numbers are:
- 1, 4, 1010 (number)10 is an even natural number following 9 and preceding 11.-In mathematics:Ten is a composite number, its proper divisors being , and...
, 2020 (number)20 is the natural number following 19 and preceding 21. A group of twenty units may also be referred to as a score.-In mathematics:*20 is the basis for vigesimal number systems....
, 3535 (number)35 is the natural number following 34 and preceding 36.- In mathematics :35 is the sum of the first five triangular numbers, making it a tetrahedral number....
, 5656 (number)56 is the natural number following 55 and preceding 57.- Mathematics :56 is the sum of the first six triangular numbers , as well as the sum of six consecutive primes . It is also a tetranacci number and a pronic number. Adding up the divisors of 1 through 8 gives 56...
, 8484 (number)84 is the natural number following 83 and preceding 85.- In mathematics :Eighty-four is the sum of the first seven triangular numbers , as well as the sum of a twin prime...
, 120120 (number)120 is the natural number following 119 and preceding 121. 120 was known as "the great hundred", especially prior to the year 1700, from the Teutonic Hundert which equalled 120. The number 100, now known commonly as "one hundred" was then known as "the small hundred". It is also known as...
, 165165 (number)165 is the natural number following 164 and preceding 166.-In mathematics:* 165 is an odd number* 165 is a composite number* 165 is a deficient number* 165 is a binary palindromic number * 165 is a sphenic number...
, 220220 (number)220 is the natural number following 219 and preceding 221.-In mathematics:It is a composite number, with its divisors being 1, 2, 4, 5, 10, 11, 20, 22, 44, 55 and 110, making it an amicable number with 284...
, 286, 364, 455, 560, 680, 816, 969, …
The formula for the n-th tetrahedral number is represented by the 3rd Rising Factorial
Pochhammer symbol
In mathematics, the Pochhammer symbol introduced by Leo August Pochhammer is the notation ', where is a non-negative integer. Depending on the context the Pochhammer symbol may represent either the rising factorial or the falling factorial as defined below. Care needs to be taken to check which...
divided by the 3rd Factorial
Factorial
In mathematics, the factorial of a non-negative integer n, denoted by n!, is the product of all positive integers less than or equal to n...
.
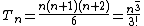
Tetrahedral numbers are found in the fourth position either from left to right or right to left in Pascal's triangle
Pascal's triangle
In mathematics, Pascal's triangle is a triangular array of the binomial coefficients in a triangle. It is named after the French mathematician, Blaise Pascal...
. The tetrahedral numbers are therefore binomial coefficient
Binomial coefficient
In mathematics, binomial coefficients are a family of positive integers that occur as coefficients in the binomial theorem. They are indexed by two nonnegative integers; the binomial coefficient indexed by n and k is usually written \tbinom nk , and it is the coefficient of the x k term in...
s:
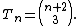
Tetrahedral numbers can be modelled by stacking spheres. For example, the fifth tetrahedral number (T5 = 35) can be modelled with 35 billiard ball
Billiard ball
A billiard ball is a small, hard ball used in cue sports, such as carom billiards, pool, and snooker. The number, type, diameter, color, and pattern of the balls differ depending upon the specific game being played...
s and the standard triangular billiards ball frame that holds 15 balls in place. Then 10 more balls are stacked on top of those, then another 6, then another three and one ball at the top completes the tetrahedron.
A.J. Meyl proved in 1878 that only three tetrahedral numbers are also perfect squares
Square number
In mathematics, a square number, sometimes also called a perfect square, is an integer that is the square of an integer; in other words, it is the product of some integer with itself...
, namely:
- T1 = 1² = 1
- T2 = 2² = 4
- T48 = 140² = 19600.
The only tetrahedral number that is also a square pyramidal number
Square pyramidal number
In mathematics, a pyramid number, or square pyramidal number, is a figurate number that represents the number of stacked spheres in a pyramid with a square base...
is 1 (Beukers, 1988), and the only tetrahedral number that is also a perfect cube is 1.
Another interesting fact about tetrahedral numbers is that the infinite sum of their reciprocals is 3/2, which can be derived using telescoping series.
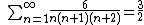
The tetrahedron with basic length 4 (summing up to 20) can be looked at as the 3-dimensional analogue of the tetractys
Tetractys
The tetractys , or tetrad, is a triangular figure consisting of ten points arranged in four rows: one, two, three, and four points in each row...
, the 4th triangular number
Triangular number
A triangular number or triangle number numbers the objects that can form an equilateral triangle, as in the diagram on the right. The nth triangle number is the number of dots in a triangle with n dots on a side; it is the sum of the n natural numbers from 1 to n...
(summing up to 10).
When order-n tetrahedra built from Tn spheres are used as a unit, it can be shown that a space tiling with such units can achieve a densest sphere packing
Sphere packing
In geometry, a sphere packing is an arrangement of non-overlapping spheres within a containing space. The spheres considered are usually all of identical size, and the space is usually three-dimensional Euclidean space...
as long as n ≤ 4.
The parity of tetrahedral numbers follows the repeating pattern odd-even-even-even.
An observation of tetrahedral numbers:
T5 = T4 + T3 + T2 + T1
Numbers that are both triangular and tetrahedral must satisfy the binomial coefficient equation:
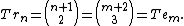
The following are the only numbers that are both Tetrahedral and Triangular numbers:
Tetrahedron1 = Triangle1 = 1
Tetrahedron3 = Triangle4 = 10
Tetrahedron8 = Triangle15 = 120
Tetrahedron20 = Triangle55 = 1540
Tetrahedron34 = Triangle119 = 7140
External links
- Geometric Proof of the Tetrahedral Number Formula by Jim Delany, The Wolfram Demonstrations Project.

