In geometry

Geometry

Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....

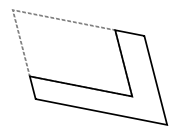
, a gnomon is a plane figure formed by removing a similar

Similarity (geometry)

Two geometrical objects are called similar if they both have the same shape. More precisely, either one is congruent to the result of a uniform scaling of the other...

 parallelogram

Parallelogram

In Euclidean geometry, a parallelogram is a convex quadrilateral with two pairs of parallel sides. The opposite or facing sides of a parallelogram are of equal length and the opposite angles of a parallelogram are of equal measure...

 from a corner of a larger parallelogram. More generically, the term gnomon denotes the form that is to be added to a figure to produce a larger figure of the same shape.

Building figurative numbers

Figurate numbers were a concern of Pythagorean geometry

Pythagoras

Pythagoras of Samos was an Ionian Greek philosopher, mathematician, and founder of the religious movement called Pythagoreanism. Most of the information about Pythagoras was written down centuries after he lived, so very little reliable information is known about him...

, since Pythagoras is credited with initiating them, and the notion that these numbers are generated from a gnomon or basic unit. The gnomon is the piece which needs to be added to a figurate number to transform it to the next bigger one.

For example, the gnomon of the square number is the odd number, of the general form 2n + 1, n = 1, 2, 3, ... . The square of size 8 composed of gnomons looks like this:










To transform from the n-square (the square of size n) to the (n + 1)-square, one adjoins 2n + 1 elements: one to the end of each row (n elements), one to the end of each column (n elements), and a single one to the corner. For example, when transforming the 7-square to the 8-square, we add 15 elements; these adjunctions are the 8s in the above figure.

Note that this gnomonic technique also provides a proof

Mathematical proof

In mathematics, a proof is a convincing demonstration that some mathematical statement is necessarily true. Proofs are obtained from deductive reasoning, rather than from inductive or empirical arguments. That is, a proof must demonstrate that a statement is true in all cases, without a single...

 that the sum of the first n odd numbers is n²; the figure illustrates 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 = 64 = 8².

See also

• Golden gnomon
• Pythagorean
  Pythagorean
  Pythagorean means of or pertaining to the ancient Ionian mathematician, philosopher, and music theorist Pythagoras. See:-Philosophy:* Pythagoreanism is a term used for the esoteric and metaphysical beliefs purported to have been held by Pythagoras....
  
  
• Pythagorean triple
  Pythagorean triple
  A Pythagorean triple consists of three positive integers a, b, and c, such that . Such a triple is commonly written , and a well-known example is . If is a Pythagorean triple, then so is for any positive integer k. A primitive Pythagorean triple is one in which a, b and c are pairwise coprime...
  
  
• Figurate number
  Figurate number
  The term figurate number is used by different writers for members of different sets of numbers, generalizing from triangular numbers to different shapes and different dimensions...