
Klein quartic
Encyclopedia

Hyperbolic geometry
In mathematics, hyperbolic geometry is a non-Euclidean geometry, meaning that the parallel postulate of Euclidean geometry is replaced...
, the Klein quartic, named after Felix Klein
Felix Klein
Christian Felix Klein was a German mathematician, known for his work in group theory, function theory, non-Euclidean geometry, and on the connections between geometry and group theory...
, is a compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
Riemann surface
Riemann surface
In mathematics, particularly in complex analysis, a Riemann surface, first studied by and named after Bernhard Riemann, is a one-dimensional complex manifold. Riemann surfaces can be thought of as "deformed versions" of the complex plane: locally near every point they look like patches of the...
of genus
Genus (mathematics)
In mathematics, genus has a few different, but closely related, meanings:-Orientable surface:The genus of a connected, orientable surface is an integer representing the maximum number of cuttings along non-intersecting closed simple curves without rendering the resultant manifold disconnected. It...
3 with the highest possible order automorphism group for this genus, namely order 168 orientation-preserving automorphisms, and 336 automorphisms if orientation may be reversed. As such, the Klein quartic is the Hurwitz surface
Hurwitz surface
In Riemann surface theory and hyperbolic geometry, a Hurwitz surface, named after Adolf Hurwitz, is a compact Riemann surface with preciselyautomorphisms, where g is the genus of the surface. This number is maximal by virtue of Hurwitz's theorem on automorphisms...
of lowest possible genus; see Hurwitz's automorphisms theorem. Its (orientation-preserving) automorphism group is isomorphic to PSL(2,7)
PSL(2,7)
In mathematics, the projective special linear group PSL is a finite simple group that has important applications in algebra, geometry, and number theory. It is the automorphism group of the Klein quartic as well as the symmetry group of the Fano plane...
, the second-smallest non-abelian simple group
Simple group
In mathematics, a simple group is a nontrivial group whose only normal subgroups are the trivial group and the group itself. A group that is not simple can be broken into two smaller groups, a normal subgroup and the quotient group, and the process can be repeated...
. The quartic was first described in .
Klein's quartic occurs in many branches of mathematics, in contexts including representation theory
Representation theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
, homology theory
Homology theory
In mathematics, homology theory is the axiomatic study of the intuitive geometric idea of homology of cycles on topological spaces. It can be broadly defined as the study of homology theories on topological spaces.-The general idea:...
, octonion multiplication, Fermat's last theorem
Fermat's Last Theorem
In number theory, Fermat's Last Theorem states that no three positive integers a, b, and c can satisfy the equation an + bn = cn for any integer value of n greater than two....
, and the Stark–Heegner theorem
Stark–Heegner theorem
In number theory, a branch of mathematics, the Stark–Heegner theorem states precisely which quadratic imaginary number fields admit unique factorisation in their ring of integers...
on imaginary quadratic number fields of class number one; see for a survey of properties.
Closed and open forms
It is important to distinguish two different forms of the quartic. The closedClosed manifold
In mathematics, a closed manifold is a type of topological space, namely a compact manifold without boundary. In contexts where no boundary is possible, any compact manifold is a closed manifold....
quartic is what is generally meant in geometry; topologically it has genus 3 and is a compact space
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
. The open or "punctured" quartic is of interest in number theory; topologically it is a genus 3 surface with 24 punctures, and geometrically these punctures are cusps
Cusp neighborhood
In mathematics, a cusp neighborhood is defined as a set of points near a cusp.-Cusp neighborhood for a Riemann surface:The cusp neighborhood for a hyperbolic Riemann surface can be defined in terms of its Fuchsian model....
. The open quartic may be obtained (topologically) from the closed quartic by puncturing at the 24 centers of the tiling by regular heptagons, as discussed below. The open and closed quartics have different metrics, though they are both hyperbolic and complete – geometrically, the cusps are "points at infinity", not holes, hence the open quartic is still complete, because these points cannot be reached.
As an algebraic curve
The Klein quartic can be viewed as an algebraic curveAlgebraic curve
In algebraic geometry, an algebraic curve is an algebraic variety of dimension one. The theory of these curves in general was quite fully developed in the nineteenth century, after many particular examples had been considered, starting with circles and other conic sections.- Plane algebraic curves...
over the complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s C, defined by the following quartic equation in homogeneous coordinates
Homogeneous coordinates
In mathematics, homogeneous coordinates, introduced by August Ferdinand Möbius in his 1827 work Der barycentrische Calcül, are a system of coordinates used in projective geometry much as Cartesian coordinates are used in Euclidean geometry. They have the advantage that the coordinates of points,...
:

Quaternion algebra construction
The compact Klein quartic can be constructed as the quotient of the hyperbolic planeHyperbolic geometry
In mathematics, hyperbolic geometry is a non-Euclidean geometry, meaning that the parallel postulate of Euclidean geometry is replaced...
by the action of a suitable Fuchsian group
Fuchsian group
In mathematics, a Fuchsian group is a discrete subgroup of PSL. The group PSL can be regarded as a group of isometries of the hyperbolic plane, or conformal transformations of the unit disc, or conformal transformations of the upper half plane, so a Fuchsian group can be regarded as a group acting...
Γ(I) which is the principal congruence subgroup
Congruence subgroup
In mathematics, a congruence subgroup of a matrix group with integer entries is a subgroup defined by congruence conditions on the entries. A very simple example would be invertible 2x2 integer matrices of determinant 1, such that the off-diagonal entries are even.An importance class of congruence...
associated with the ideal
 in the ring of integers
in the ring of integers  of the field
of the field  where
where  . Note the identity
. Note the identity
exhibiting
 as a prime factor of 7 in the ring of integers.
as a prime factor of 7 in the ring of integers.The group Γ(I) is a subgroup of the (2,3,7)
(2,3,7) triangle group
In the theory of Riemann surfaces and hyperbolic geometry, the triangle group is particularly important. This importance stems from its connection to Hurwitz surfaces, namely Riemann surfaces of genus g with the largest possible order, 84, of its automorphism group.A note on terminology – the "...
hyperbolic triangle group
Triangle group
In mathematics, a triangle group is a group that can be realized geometrically by sequences of reflections across the sides of a triangle. The triangle can be an ordinary Euclidean triangle, a triangle on the sphere, or a hyperbolic triangle...
. Namely, Γ(I) is a subgroup of the group of norm 1 elements in the quaternion algebra generated as an associative algebra by the generators i,j and relations
 . One chooses a suitable Hurwitz quaternion order
. One chooses a suitable Hurwitz quaternion orderHurwitz quaternion order
The Hurwitz quaternion order is a specific order in a quaternion algebra over a suitable number field. The order is of particular importance in Riemann surface theory, in connection with surfaces with maximal symmetry, namely the Hurwitz surfaces. The Hurwitz quaternion order was studied in 1967...
 in the quaternion algebra, Γ(I) is then the group of norm 1 elements in
in the quaternion algebra, Γ(I) is then the group of norm 1 elements in  . The least absolute value of a trace of a hyperbolic element in Γ(I) is
. The least absolute value of a trace of a hyperbolic element in Γ(I) is  , corresponding the value 3.936 for the systole of the Klein quartic, one of the highest in this genus.
, corresponding the value 3.936 for the systole of the Klein quartic, one of the highest in this genus.Tiling

Regular map (graph theory)
In mathematics, a regular map is a symmetric tessellation of a closed surface. More precisely, a regular map is a decomposition of a two-dimensional manifold such as a sphere, torus, or Klein bottle into topological disks, such that every flag can be transformed into any other flag by a symmetry...
"), and these are used in understanding the symmetry group, dating back to Klein's original paper. Given a fundamental domain
Fundamental domain
In geometry, the fundamental domain of a symmetry group of an object is a part or pattern, as small or irredundant as possible, which determines the whole object based on the symmetry. More rigorously, given a topological space and a group acting on it, the images of a single point under the group...
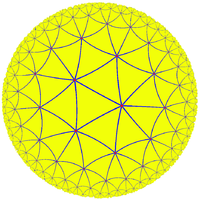
for the group action (for the full, orientation-reversing symmetry group, a (2,3,7) triangle), the reflection domains (images of this domain under the group) give a tiling of the quartic such that the automorphism group of the tiling equals the automorphism group of the surface – reflections in the lines of the tiling correspond to the reflections in the group (reflections in the lines of a given fundamental triangle give a set of 3 generating reflections). This tiling is a quotient of the order-3 bisected heptagonal tiling
Order-3 bisected heptagonal tiling
In geometry, the order-3 bisected heptagonal tiling is a semiregular dual tiling of the hyperbolic plane. It is constructed by congruent right triangles with 4, 6, and 14 triangles meeting at each vertex....
of the hyperbolic plane
Hyperbolic geometry
In mathematics, hyperbolic geometry is a non-Euclidean geometry, meaning that the parallel postulate of Euclidean geometry is replaced...
(the universal cover of the quartic), and all Hurwitz surfaces are tiled in the same way, as quotients.
This tiling is uniform but not regular (it is by scalene triangles), and often regular tilings are used instead. A quotient of any tiling in the (2,3,7) family can be used (and will have the same automorphism group); of these, the two regular tilings are the tiling by 24 regular hyperbolic heptagons, each of degree 3 (meeting at 56 vertices), and the dual tiling by 56 equilateral triangles, each of degree 7 (meeting at 24 vertices). The order of the automorphism group is related, being the number of polygons times the number of edges in the polygon in both cases.
- 24 × 7 = 168
- 56 × 3 = 168
The covering tilings on the hyperbolic plane are the order-3 heptagonal tiling and the order-7 triangular tiling.
The automorphism group can be augmented (by a symmetry which is not realized by a symmetry of the tiling) to yield the Mathieu group
Mathieu group
In the mathematical field of group theory, the Mathieu groups, named after the French mathematician Émile Léonard Mathieu, are five finite simple groups he discovered and reported in papers in 1861 and 1873; these were the first sporadic simple groups discovered...
M24.
Corresponding to each tiling of the quartic (partition of the quartic variety into subsets) is an abstract polyhedron, which abstracts from the geometry and only reflects the combinatorics of the tiling (this is a general way of obtaining an abstract polytope
Abstract polytope
In mathematics, an abstract polytope, informally speaking, is a structure which considers only the combinatorial properties of a traditional polytope, ignoring many of its other properties, such as angles, edge lengths, etc...
from a tiling) – the vertices, edges, and faces of the polyhedron are equal as sets to the vertices, edges, and faces of the tiling, with the same incidence relations, and the (combinatorial) automorphism group of the abstract polyhedron equals the (geometric) automorphism group of the quartic. In this way the geometry reduces to combinatorics.
Affine quartic
The above is a tiling of the projective quartic (a closed manifold); the affine quartic has 24 cusps (topologically, punctures), which correspond to the 24 vertices of the regular triangular tiling, or equivalently the centers of the 24 heptagons of the in the hepatgonal tiling, and can be realized as follows.Considering the action of SL(2,R) on the upper half-plane model
Poincaré half-plane model
In non-Euclidean geometry, the Poincaré half-plane model is the upper half-plane , together with a metric, the Poincaré metric, that makes it a model of two-dimensional hyperbolic geometry....
H2 of the hyperbolic plane
Hyperbolic geometry
In mathematics, hyperbolic geometry is a non-Euclidean geometry, meaning that the parallel postulate of Euclidean geometry is replaced...
by Möbius transformations, the affine Klein quartic can be realized as the quotient Γ(7)\H2. (Here Γ(7) is the congruence subgroup
Congruence subgroup
In mathematics, a congruence subgroup of a matrix group with integer entries is a subgroup defined by congruence conditions on the entries. A very simple example would be invertible 2x2 integer matrices of determinant 1, such that the off-diagonal entries are even.An importance class of congruence...
of SL(2,Z) consisting of matrices that are congruent to the identity matrix when all entries are taken modulo
Modular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
7.)
3-dimensional models
The Klein quartic cannot be realized as a 3-dimensional figure, in the sense that no 3-dimensional figure has (rotational) symmetries equal to PSL(2,7), since PSL(2,7) does not embed as a subgroup of SO(3) (or O(3)) – it does not have a (non-trivial) 3-dimensional linear representation.However, many 3-dimensional models of the Klein quartic have been given, starting in Klein's original paper, which seek to demonstrate features of the quartic and preserve the symmetries topologically, though not all geometrically. The resulting models most often have either tetrahedral (order 12) or octahedral (order 24) symmetries; the remaining order 7 symmetry cannot be as easily visualized, and in fact is the title of Klein's paper.
Most often, the quartic is modeled either by a smooth genus 3 surface with tetrahedral symmetry (replacing the edges of a regular tetrahedron with tubes/handles yields such a shape), which have been dubbed "tetruses", or by polyhedral approximations, which have been dubbed "tetroids"; in both cases this is an embedding of the shape in 3 dimensions. The most notable smooth model (tetrus) is the sculpture The Eightfold Way by Helaman Ferguson
Helaman Ferguson
Helaman Rolfe Pratt Ferguson is an American sculptor and a digital artist, specifically an algorist.Ferguson's mother died when he was about three and his father went off to serve in the Second World War. He was adopted and raised in New York. He was a graduate of Hamilton College and received a...
at the Mathematical Sciences Research Institute
Mathematical Sciences Research Institute
The Mathematical Sciences Research Institute , founded in 1982, is an independent nonprofit mathematical research institution whose funding sources include the National Science Foundation, foundations, corporations, and more than 90 universities and institutions...
in Berkeley, California
Berkeley, California
Berkeley is a city on the east shore of the San Francisco Bay in Northern California, United States. Its neighbors to the south are the cities of Oakland and Emeryville. To the north is the city of Albany and the unincorporated community of Kensington...
, made of marble and serpentine, and unveiled on November 14, 1993. The title refers to the fact that starting at any vertex of the triangulated surface and moving along any edge, if you alternately turn left and right when reaching a vertex, you always return to the original point after eight edges. The acquisition of the sculpture led in due course to the publication of a book of papers , detailing properties of the quartic and containing the first English translation of Klein's paper. Polyhedral models with tetrahedral symmetry most often have convex hull
Convex hull
In mathematics, the convex hull or convex envelope for a set of points X in a real vector space V is the minimal convex set containing X....
a truncated tetrahedron
Truncated tetrahedron
In geometry, the truncated tetrahedron is an Archimedean solid. It has 4 regular hexagonal faces, 4 regular triangular faces, 12 vertices and 18 edges.- Area and volume :...
– see and for examples and illustrations. Some of these models consist of 20 triangles or 56 triangles (abstractly, the regular skew polyhedron
Regular skew polyhedron
In geometry, the regular skew polyhedra are generalizations to the set of regular polyhedron which include the possibility of nonplanar faces or vertex figures....
{3,7|,4}, with 56 faces, 84 edges, and 24 vertices), which cannot be realized as equilateral, with twists in the arms of the tetrahedron; while others have 24 heptagons – these heptagons can be taken to be planar, though non-convex, and the models are more complex than the triangular ones because the complexity is reflected in the shapes of the (non-flexible) heptagonal faces, rather than in the (flexible) vertices.

Truncated cube
In geometry, the truncated cube, or truncated hexahedron, is an Archimedean solid. It has 14 regular faces , 36 edges, and 24 vertices....
, the snub cube
Snub cube
In geometry, the snub cube, or snub cuboctahedron, is an Archimedean solid.The snub cube has 38 faces, 6 of which are squares and the other 32 are equilateral triangles. It has 60 edges and 24 vertices. It is a chiral polyhedron, that is, it has two distinct forms, which are mirror images of each...
, or the rhombicuboctahedron
Rhombicuboctahedron
In geometry, the rhombicuboctahedron, or small rhombicuboctahedron, is an Archimedean solid with eight triangular and eighteen square faces. There are 24 identical vertices, with one triangle and three squares meeting at each. Note that six of the squares only share vertices with the triangles...
, as in the small cubicuboctahedron
Small cubicuboctahedron
In geometry, the small cubicuboctahedron is a uniform star polyhedron, indexed as U13. It has 20 faces , 48 edges, and 24 vertices. Its vertex figure is a crossed quadrilateral.- Related polyhedra :...
at right. The small cubicuboctahedron immersion is obtained by joining some of the triangles (2 triangles form a square, 6 form an octagon), which can be visualized by coloring the triangles (the corresponding tiling is topologically but not geometrically the t0,1{4, 3, 3} tiling). This immersion can also be used to geometrically construct the Mathieu group
Mathieu group
In the mathematical field of group theory, the Mathieu groups, named after the French mathematician Émile Léonard Mathieu, are five finite simple groups he discovered and reported in papers in 1861 and 1873; these were the first sporadic simple groups discovered...
M24 by adding to PSL(2,7) the permutation which interchanges opposite points of the bisecting lines of the squares and octagons.
Dessin d'enfants
The dessin d'enfantDessin d'enfant
In mathematics, a dessin d'enfant is a type of graph drawing used to study Riemann surfaces and to provide combinatorial invariants for the action of the absolute Galois group of the rational numbers.Intuitively, a dessin d'enfant is simply a graph, with its vertices colored alternating black and...
on the Klein quartic associated with the quotient map by its automorphism group (with quotient the Riemann sphere) is precisely the 1-skeleton of the order-3 heptagonal tiling. That is, the quotient map is ramified over the points 0, 1728, and ∞; dividing by 1728 yields a Belyi function (ramified at 0, 1, and ∞), where the 56 vertices (black points in dessin) lie over 0, the midpoints of the 84 edges (white points in dessin) lie over 1, and the centers of the 24 heptagons lie over infinity. The resulting dessin is a "platonic" dessin, meaning edge-transitive and "clean" (each white point has valence 2).
Related surfaces
The Klein quartic is related to various other surfaces.Geometrically, it is the smallest Hurwitz surface
Hurwitz surface
In Riemann surface theory and hyperbolic geometry, a Hurwitz surface, named after Adolf Hurwitz, is a compact Riemann surface with preciselyautomorphisms, where g is the genus of the surface. This number is maximal by virtue of Hurwitz's theorem on automorphisms...
(lowest genus); the next is the Macbeath surface
Macbeath surface
In Riemann surface theory and hyperbolic geometry, the Macbeath surface, also called Macbeath's curve or the Fricke–Macbeath curve, is the genus-7 Hurwitz surface....
(genus 7), and the following is the First Hurwitz triplet
First Hurwitz triplet
In the mathematical theory of Riemann surfaces, the first Hurwitz triplet is a triple of distinct Hurwitz surfaces with the identical automorphism group of the lowest possible genus, namely 14 . The explanation for this phenomenon is arithmetic...
(3 surfaces of genus 14). More generally, it is the most symmetric surface of a given genus (being a Hurwitz surface); in this class, the Bolza surface
Bolza surface
In mathematics, the Bolza surface, alternatively, complex algebraic Bolza curve , is a compact Riemann surface of genus 2 with the highest possible order of the conformal automorphism group in this genus, namely 48. An affine model for the Bolza surface can be obtained as the locus of the...
is the most symmetric genus 2 surface, while Bring's surface is a highly symmetric genus 4 surface – see isometries of Riemann surfaces for further discussion.
Algebraically, the (affine) Klein quartic is the modular curve
Modular curve
In number theory and algebraic geometry, a modular curve Y is a Riemann surface, or the corresponding algebraic curve, constructed as a quotient of the complex upper half-plane H by the action of a congruence subgroup Γ of the modular group of integral 2×2 matrices SL...
X(7) and the projective Klein quartic is its compactification, just as the dodecahedron (with a cusp in the center of each face) is the modular curve X(5); this explains the relevance for number theory.
More subtly, the (projective) Klein quartic is a Shimura curve (as are the Hurwitz surface of genus 7 and 14), and as such parametrizes principally polarized abelian varieties of dimension 6.
There are also other quartic surface
Quartic surface
In mathematics, especially in algebraic geometry, a quartic surface is a surface defined by an equation of degree 4.More specifically there are two closely related types of quartic surface: affine and projective...
s of interest – see special quartic surfaces.
More exceptionally, the Klein quartic forms part of a "trinity" in the sense of Vladimir Arnold
Vladimir Arnold
Vladimir Igorevich Arnold was a Soviet and Russian mathematician. While he is best known for the Kolmogorov–Arnold–Moser theorem regarding the stability of integrable Hamiltonian systems, he made important contributions in several areas including dynamical systems theory, catastrophe theory,...
, which can also be described as a McKay correspondence. In this collection, the projective special linear groups PSL(2,5), PSL(2,7), and PSL(2,11) (orders 60, 168, 660) are analogous, corresponding to icosahedral symmetry
Icosahedral symmetry
A regular icosahedron has 60 rotational symmetries, and a symmetry order of 120 including transformations that combine a reflection and a rotation...
(genus 0), the symmetries of the Klein quartic (genus 2), and the buckyball surface (genus 70). These are further connected to many other exceptional phenomena, which is elaborated at "trinities".
External links
- Klein's Quartic Curve, John Baez, July 28, 2006
- Klein's Quartic Curve, by Greg Egan – illustrations

