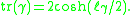(2,3,7) triangle group
Encyclopedia
In the theory of Riemann surfaces and hyperbolic geometry
, the triangle group
(2,3,7) is particularly important. This importance stems from its connection to Hurwitz surfaces, namely Riemann surfaces of genus g with the largest possible order, 84(g-1), of its automorphism group.
A note on terminology – the "(2,3,7) triangle group" most often refers, not to the full triangle group Δ(2,3,7) (the Coxeter group with Schwarz triangle
(2,3,7) or a realization as a hyperbolic reflection group
), but rather to the ordinary triangle group (the von Dyck group) D(2,3,7) of orientation-preserving maps (the rotation group), which is index 2.
Torsion-free normal subgroups of the (2,3,7) triangle group are Fuchsian group
s associated with Hurwitz surface
s, such as the Klein quartic
, Macbeath surface
and First Hurwitz triplet
.
To construct the triangle group, start with a hyperbolic triangle with angles π/2, π/3, π/7. This triangle, the smallest hyperbolic Schwarz triangle
, tiles the plane by reflections in its sides. Consider then the group generated by reflections in the sides of the triangle, which (since the triangle tiles) is a non-Euclidean crystallographic group
(discrete subgroup of hyperbolic isometries) with this triangle for fundamental domain
; the associated tiling is the order-3 bisected heptagonal tiling
. The (2,3,7) triangle group is defined as the index
2 subgroup consisting of the orientation-preserving isometries, which is a Fuchsian group
(orientation-preserving NEC group).
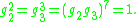
Geometrically, these correspond to rotations by 2π/2, 2π/3, 2π/7 about the vertices of the Schwarz triangle.
. More specifically, the triangle group is the quotient of the group of quaternions by its center ±1.
Let η=2cos(2π/7). Then from the identity
we see that Q(η) is a totally real cubic extension of Q. The (2,3,7) hyperbolic triangle group
is a subgroup of the group of norm 1 elements in the quaternion algebra generated as an associative algebra by the pair of generators i,j and relations i² = j² = η, ij=-ji. One chooses a suitable Hurwitz quaternion order
in the quaternion algebra. Here the order 
is generated by elements
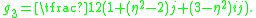
In fact, the order is a free Z[η]-module over the basis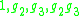
. Here the generators satisfy the relations
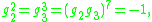
which descend to the appropriate relations in the triangle group, after quotienting by the center.
in SL(2,R), specifically as a quotient of the modular group
. This can be visualized by the associated tilings, as depicted at right: the (2,3,7) tiling on the Poincaré disc is a quotient of the modular tiling on the upper half-plane.
However, for many purposes, explicit isomorphisms are unnecessary. Thus, traces of group elements (and hence also translation lengths of hyperbolic elements acting in the upper half-plane, as well as systoles of Fuchsian subgroups) can be calculated by means of the reduced trace in the quaternion algebra, and the formula
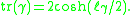
Hyperbolic geometry
In mathematics, hyperbolic geometry is a non-Euclidean geometry, meaning that the parallel postulate of Euclidean geometry is replaced...
, the triangle group
Triangle group
In mathematics, a triangle group is a group that can be realized geometrically by sequences of reflections across the sides of a triangle. The triangle can be an ordinary Euclidean triangle, a triangle on the sphere, or a hyperbolic triangle...
(2,3,7) is particularly important. This importance stems from its connection to Hurwitz surfaces, namely Riemann surfaces of genus g with the largest possible order, 84(g-1), of its automorphism group.
A note on terminology – the "(2,3,7) triangle group" most often refers, not to the full triangle group Δ(2,3,7) (the Coxeter group with Schwarz triangle
Schwarz triangle
In geometry, a Schwarz triangle, named after Hermann Schwarz is a spherical triangle that can be used to tile a sphere, possibly overlapping, through reflections in its edges. They were classified in ....
(2,3,7) or a realization as a hyperbolic reflection group
Reflection group
In group theory and geometry, a reflection group is a discrete group which is generated by a set of reflections of a finite-dimensional Euclidean space. The symmetry group of a regular polytope or of a tiling of the Euclidean space by congruent copies of a regular polytope is necessarily a...
), but rather to the ordinary triangle group (the von Dyck group) D(2,3,7) of orientation-preserving maps (the rotation group), which is index 2.
Torsion-free normal subgroups of the (2,3,7) triangle group are Fuchsian group
Fuchsian group
In mathematics, a Fuchsian group is a discrete subgroup of PSL. The group PSL can be regarded as a group of isometries of the hyperbolic plane, or conformal transformations of the unit disc, or conformal transformations of the upper half plane, so a Fuchsian group can be regarded as a group acting...
s associated with Hurwitz surface
Hurwitz surface
In Riemann surface theory and hyperbolic geometry, a Hurwitz surface, named after Adolf Hurwitz, is a compact Riemann surface with preciselyautomorphisms, where g is the genus of the surface. This number is maximal by virtue of Hurwitz's theorem on automorphisms...
s, such as the Klein quartic
Klein quartic
In hyperbolic geometry, the Klein quartic, named after Felix Klein, is a compact Riemann surface of genus 3 with the highest possible order automorphism group for this genus, namely order 168 orientation-preserving automorphisms, and 336 automorphisms if orientation may be reversed...
, Macbeath surface
Macbeath surface
In Riemann surface theory and hyperbolic geometry, the Macbeath surface, also called Macbeath's curve or the Fricke–Macbeath curve, is the genus-7 Hurwitz surface....
and First Hurwitz triplet
First Hurwitz triplet
In the mathematical theory of Riemann surfaces, the first Hurwitz triplet is a triple of distinct Hurwitz surfaces with the identical automorphism group of the lowest possible genus, namely 14 . The explanation for this phenomenon is arithmetic...
.
Hyperbolic construction
Schwarz triangle
In geometry, a Schwarz triangle, named after Hermann Schwarz is a spherical triangle that can be used to tile a sphere, possibly overlapping, through reflections in its edges. They were classified in ....
, tiles the plane by reflections in its sides. Consider then the group generated by reflections in the sides of the triangle, which (since the triangle tiles) is a non-Euclidean crystallographic group
Non-Euclidean crystallographic group
In mathematics, a non-Euclidean crystallographic group, NEC group or N.E.C. group is a discrete group of isometries of the hyperbolic plane. These symmetry groups correspond to the wallpaper groups in euclidean geometry...
(discrete subgroup of hyperbolic isometries) with this triangle for fundamental domain
Fundamental domain
In geometry, the fundamental domain of a symmetry group of an object is a part or pattern, as small or irredundant as possible, which determines the whole object based on the symmetry. More rigorously, given a topological space and a group acting on it, the images of a single point under the group...
; the associated tiling is the order-3 bisected heptagonal tiling
Order-3 bisected heptagonal tiling
In geometry, the order-3 bisected heptagonal tiling is a semiregular dual tiling of the hyperbolic plane. It is constructed by congruent right triangles with 4, 6, and 14 triangles meeting at each vertex....
. The (2,3,7) triangle group is defined as the index
Index of a subgroup
In mathematics, specifically group theory, the index of a subgroup H in a group G is the "relative size" of H in G: equivalently, the number of "copies" of H that fill up G. For example, if H has index 2 in G, then intuitively "half" of the elements of G lie in H...
2 subgroup consisting of the orientation-preserving isometries, which is a Fuchsian group
Fuchsian group
In mathematics, a Fuchsian group is a discrete subgroup of PSL. The group PSL can be regarded as a group of isometries of the hyperbolic plane, or conformal transformations of the unit disc, or conformal transformations of the upper half plane, so a Fuchsian group can be regarded as a group acting...
(orientation-preserving NEC group).
Group presentation
It has a presentation in terms of a pair of generators, g2, g3, modulo the following relations: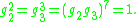Geometrically, these correspond to rotations by 2π/2, 2π/3, 2π/7 about the vertices of the Schwarz triangle.
Quaternion algebra
The (2,3,7) triangle group admits a presentation in terms of the group of quaternions of norm 1 in a suitable order in a quaternion algebraQuaternion algebra
In mathematics, a quaternion algebra over a field F is a central simple algebra A over F that has dimension 4 over F. Every quaternion algebra becomes the matrix algebra by extending scalars , i.e...
. More specifically, the triangle group is the quotient of the group of quaternions by its center ±1.
Let η=2cos(2π/7). Then from the identity
we see that Q(η) is a totally real cubic extension of Q. The (2,3,7) hyperbolic triangle group
Triangle group
In mathematics, a triangle group is a group that can be realized geometrically by sequences of reflections across the sides of a triangle. The triangle can be an ordinary Euclidean triangle, a triangle on the sphere, or a hyperbolic triangle...
is a subgroup of the group of norm 1 elements in the quaternion algebra generated as an associative algebra by the pair of generators i,j and relations i² = j² = η, ij=-ji. One chooses a suitable Hurwitz quaternion order
Hurwitz quaternion order
The Hurwitz quaternion order is a specific order in a quaternion algebra over a suitable number field. The order is of particular importance in Riemann surface theory, in connection with surfaces with maximal symmetry, namely the Hurwitz surfaces. The Hurwitz quaternion order was studied in 1967...
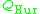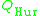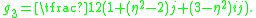
in the quaternion algebra. Here the order is generated by elementsIn fact, the order is a free Z[η]-module over the basis
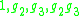. Here the generators satisfy the relations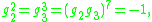which descend to the appropriate relations in the triangle group, after quotienting by the center.
Relation to SL(2,R)
Extending the scalars from Q(η) to R (via the standard imbedding), one obtains an isomorphism between the quaternion algebra and the algebra M(2,R) of real 2 by 2 matrices. Choosing a concrete isomorphism allows one to exhibit the (2,3,7) triangle group as a specific Fuchsian groupFuchsian group
In mathematics, a Fuchsian group is a discrete subgroup of PSL. The group PSL can be regarded as a group of isometries of the hyperbolic plane, or conformal transformations of the unit disc, or conformal transformations of the upper half plane, so a Fuchsian group can be regarded as a group acting...
in SL(2,R), specifically as a quotient of the modular group
Modular group
In mathematics, the modular group Γ is a fundamental object of study in number theory, geometry, algebra, and many other areas of advanced mathematics...
. This can be visualized by the associated tilings, as depicted at right: the (2,3,7) tiling on the Poincaré disc is a quotient of the modular tiling on the upper half-plane.
However, for many purposes, explicit isomorphisms are unnecessary. Thus, traces of group elements (and hence also translation lengths of hyperbolic elements acting in the upper half-plane, as well as systoles of Fuchsian subgroups) can be calculated by means of the reduced trace in the quaternion algebra, and the formula