
Order-3 bisected heptagonal tiling
Encyclopedia
In geometry
, the order-3 bisected heptagonal tiling is a semiregular dual tiling of the hyperbolic plane
. It is constructed by congruent right triangle
s with 4, 6, and 14 triangles meeting at each vertex.
The image shows a Poincaré disk model
projection of the hyperbolic plane.
It is labeled V4.6.14 because each right triangle face has three types of vertices: one with 4 triangles, one with 6 triangles, and one with 14 triangles. It is the dual tessellation of the great rhombitriheptagonal tiling which has one square and one heptagon and one tetrakaidecagon at each vertex.
, seeing it as a 3-7 rhombic tiling, divided by a kis operator, adding a center point to each rhombus, and dividing into four triangles:
s – for the heptagonal tiling, the important (2,3,7) triangle group
.
See also the uniform tilings of the hyperbolic plane with (2,3,7) symmetry.
Just as the (2,3,7) triangle group is a quotient of the modular group
(2,3,∞), the associated tiling is the quotient of the modular tiling, as depicted in the video at right.
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, the order-3 bisected heptagonal tiling is a semiregular dual tiling of the hyperbolic plane
Uniform tilings in hyperbolic plane
There are an infinite number of uniform tilings on the hyperbolic plane based on the where 1/p + 1/q + 1/r ...
. It is constructed by congruent right triangle
Right triangle
A right triangle or right-angled triangle is a triangle in which one angle is a right angle . The relation between the sides and angles of a right triangle is the basis for trigonometry.-Terminology:The side opposite the right angle is called the hypotenuse...
s with 4, 6, and 14 triangles meeting at each vertex.
The image shows a Poincaré disk model
Poincaré disk model
In geometry, the Poincaré disk model, also called the conformal disk model, is a model of n-dimensional hyperbolic geometry in which the points of the geometry are in an n-dimensional disk, or unit ball, and the straight lines of the hyperbolic geometry are segments of circles contained in the disk...
projection of the hyperbolic plane.
It is labeled V4.6.14 because each right triangle face has three types of vertices: one with 4 triangles, one with 6 triangles, and one with 14 triangles. It is the dual tessellation of the great rhombitriheptagonal tiling which has one square and one heptagon and one tetrakaidecagon at each vertex.
Naming
An alternative name is 3-7 kisrhombille by ConwayJohn Horton Conway
John Horton Conway is a prolific mathematician active in the theory of finite groups, knot theory, number theory, combinatorial game theory and coding theory...
, seeing it as a 3-7 rhombic tiling, divided by a kis operator, adding a center point to each rhombus, and dividing into four triangles:
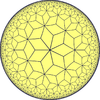
- 3-7 rhombic tiling (rhombille)
Related polyhedra and tilings
It is topologically related to a polyhedra sequence; see discussion. This group is special for having all even number of edges per vertex and form bisecting planes through the polyhedra and infinite lines in the plane, and are the reflection domains for the (2,3,n) triangle groupTriangle group
In mathematics, a triangle group is a group that can be realized geometrically by sequences of reflections across the sides of a triangle. The triangle can be an ordinary Euclidean triangle, a triangle on the sphere, or a hyperbolic triangle...
s – for the heptagonal tiling, the important (2,3,7) triangle group
(2,3,7) triangle group
In the theory of Riemann surfaces and hyperbolic geometry, the triangle group is particularly important. This importance stems from its connection to Hurwitz surfaces, namely Riemann surfaces of genus g with the largest possible order, 84, of its automorphism group.A note on terminology – the "...
.
See also the uniform tilings of the hyperbolic plane with (2,3,7) symmetry.
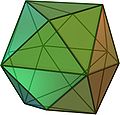 V4.6.6 Tetrakis hexahedron In geometry, a tetrakis hexahedron is a Catalan solid. Its dual is the truncated octahedron, an Archimedean solid. It can be seen as a cube with square pyramids covering each square face; that is, it is the Kleetope of the cube.... |
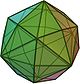 V4.6.8 Disdyakis dodecahedron In geometry, a disdyakis dodecahedron, or hexakis octahedron, is a Catalan solid and the dual to the Archimedean truncated cuboctahedron. As such it is face-transitive but with irregular face polygons... |
 V4.6.10 Disdyakis triacontahedron In geometry, a disdyakis triacontahedron, or hexakis icosahedron is a Catalan solid and the dual to the Archimedean truncated icosidodecahedron. As such it is face uniform but with irregular face polygons... |
 V4.6.12 |
Just as the (2,3,7) triangle group is a quotient of the modular group
Modular group
In mathematics, the modular group Γ is a fundamental object of study in number theory, geometry, algebra, and many other areas of advanced mathematics...
(2,3,∞), the associated tiling is the quotient of the modular tiling, as depicted in the video at right.
See also
- Hexakis triangular tilingHexakis triangular tilingIn geometry, the bisected hexagonal tiling is a tiling of the Euclidean plane. It is constructed by congruent 30-60 degree right triangles with 4, 6, and 12 triangles meeting at each vertex....
- Tilings of regular polygons
- List of uniform tilings
- Uniform tilings in hyperbolic planeUniform tilings in hyperbolic planeThere are an infinite number of uniform tilings on the hyperbolic plane based on the where 1/p + 1/q + 1/r ...

