Hexakis triangular tiling
Encyclopedia
In geometry
, the bisected hexagonal tiling is a tiling of the Euclidean plane. It is constructed by congruent 30-60 degree right triangle
s with 4, 6, and 12 triangles meeting at each vertex.
It can be seen as an equilateral hexagonal tiling with each hexagon divided into 12 triangles from the center point. (Alternately it can be seen as a bisected triangular tiling divided into 6 triangles, or as an infinite arrangement of lines
in six parallel families.)
Conway
calls it a kisrhombille for his kis vertex bisector operation applied to the rhombille tiling. More specifically it can be called a 3-6 kisrhombille, to distringuish it from other similar hyperbolic tilings, like 3-7 kisrhombille.
It is labeled V4.6.12 because each right triangle face has three types of vertices: one with 4 triangles, one with 6 triangles, and one with 12 triangles.
V4.6.2n. This group is special for having all even number of edges per vertex and form bisecting planes through the polyhedra and infinite lines in the plane, and continuing into the hyperbolic plane for any
With an even number of faces at every vertex, these polyhedra and tilings can be shown by alternating two colors so all adjacent faces have different colors.
Each face on these domains also corresponds to the fundamental domain of a symmetry group
with order 2,3,n mirrors at each triangle face vertex.
, as each of the equilateral triangles can serve as faces, the edges of which adjoin isosceles triangles that can serve as tabs for gluing the model together.
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, the bisected hexagonal tiling is a tiling of the Euclidean plane. It is constructed by congruent 30-60 degree right triangle
Right triangle
A right triangle or right-angled triangle is a triangle in which one angle is a right angle . The relation between the sides and angles of a right triangle is the basis for trigonometry.-Terminology:The side opposite the right angle is called the hypotenuse...
s with 4, 6, and 12 triangles meeting at each vertex.
It can be seen as an equilateral hexagonal tiling with each hexagon divided into 12 triangles from the center point. (Alternately it can be seen as a bisected triangular tiling divided into 6 triangles, or as an infinite arrangement of lines
Arrangement of lines
In geometry an arrangement of lines is the partition of the plane formed by a collection of lines. Bounds on the complexity of arrangements have been studied in discrete geometry, and computational geometers have found algorithms for the efficient construction of arrangements.-Definition:For any...
in six parallel families.)
Conway
John Horton Conway
John Horton Conway is a prolific mathematician active in the theory of finite groups, knot theory, number theory, combinatorial game theory and coding theory...
calls it a kisrhombille for his kis vertex bisector operation applied to the rhombille tiling. More specifically it can be called a 3-6 kisrhombille, to distringuish it from other similar hyperbolic tilings, like 3-7 kisrhombille.
It is labeled V4.6.12 because each right triangle face has three types of vertices: one with 4 triangles, one with 6 triangles, and one with 12 triangles.
Dual tiling
It is the dual tessellation of the truncated trihexagonal tiling which has one square and one hexagon and one dodecagon at each vertex.Related polyhedra and tilings
It is topologically related to a polyhedra sequence defined by the face configurationFace configuration
In geometry, a face configuration is notational description of a face-transitive polyhedron. It represents a sequential count of the number of faces that exist at each vertex around a face....
V4.6.2n. This group is special for having all even number of edges per vertex and form bisecting planes through the polyhedra and infinite lines in the plane, and continuing into the hyperbolic plane for any

With an even number of faces at every vertex, these polyhedra and tilings can be shown by alternating two colors so all adjacent faces have different colors.
Each face on these domains also corresponds to the fundamental domain of a symmetry group
Symmetry group
The symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation...
with order 2,3,n mirrors at each triangle face vertex.
| n | 2 | 3 | 4 | 5 |
|---|---|---|---|---|
| Tiling space | Spherical Sphere A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point... |
|||
| Face configuration Face configuration In geometry, a face configuration is notational description of a face-transitive polyhedron. It represents a sequential count of the number of faces that exist at each vertex around a face.... V4.6.2n |
V4.6.4 | V4.6.6 Tetrakis hexahedron In geometry, a tetrakis hexahedron is a Catalan solid. Its dual is the truncated octahedron, an Archimedean solid. It can be seen as a cube with square pyramids covering each square face; that is, it is the Kleetope of the cube.... |
V4.6.8 Disdyakis dodecahedron In geometry, a disdyakis dodecahedron, or hexakis octahedron, is a Catalan solid and the dual to the Archimedean truncated cuboctahedron. As such it is face-transitive but with irregular face polygons... |
V4.6.10 Disdyakis triacontahedron In geometry, a disdyakis triacontahedron, or hexakis icosahedron is a Catalan solid and the dual to the Archimedean truncated icosidodecahedron. As such it is face uniform but with irregular face polygons... |
| Symmetry group (Orbifold) |
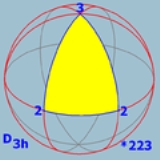
D3h (*322) D6h (*622) full sym. |
Td Tetrahedral symmetry 150px|right|thumb|A regular [[tetrahedron]], an example of a solid with full tetrahedral symmetryA regular tetrahedron has 12 rotational symmetries, and a symmetry order of 24 including transformations that combine a reflection and a rotation.The group of all symmetries is isomorphic to the group... (*332) Oh (*432) full sym. |
Oh Octahedral symmetry 150px|thumb|right|The [[cube]] is the most common shape with octahedral symmetryA regular octahedron has 24 rotational symmetries, and a symmetry order of 48 including transformations that combine a reflection and a rotation... (*432) |
Ih Icosahedral symmetry A regular icosahedron has 60 rotational symmetries, and a symmetry order of 120 including transformations that combine a reflection and a rotation... (*532) |
| Symmetry fundamental domain |
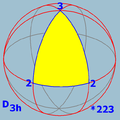 (Order 12) |
 (Order 24) |
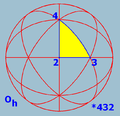 (Order 48) |
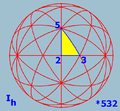 (Order 60) |
| Polyhedron |  |
|||
| Net Net (polyhedron) In geometry the net of a polyhedron is an arrangement of edge-joined polygons in the plane which can be folded to become the faces of the polyhedron... |
 |
 |
 |
 |
| n | 6 | 7 | 8 |
|---|---|---|---|
| Tiling space | Euclidean Euclidean Euclidean relates to Euclid , a town or others. It may refer to:Geometry... |
Hyperbolic Hyperbolic geometry In mathematics, hyperbolic geometry is a non-Euclidean geometry, meaning that the parallel postulate of Euclidean geometry is replaced... |
Hyperbolic |
| Face configuration Face configuration In geometry, a face configuration is notational description of a face-transitive polyhedron. It represents a sequential count of the number of faces that exist at each vertex around a face.... V4.6.2n |
V4.6.12 | V4.6.14 Order-3 bisected heptagonal tiling In geometry, the order-3 bisected heptagonal tiling is a semiregular dual tiling of the hyperbolic plane. It is constructed by congruent right triangles with 4, 6, and 14 triangles meeting at each vertex.... |
V4.6.16 |
| Symmetry group (orbifold notation) |
(*632) | (*732) | (*832) |
| Tiling |  |
 |
... |
Practical uses
The bisected hexagonal tiling is a useful starting point for making paper models of deltahedraDeltahedron
A deltahedron is a polyhedron whose faces are all equilateral triangles. The name is taken from the Greek majuscule delta , which has the shape of an equilateral triangle. There are infinitely many deltahedra, but of these only eight are convex, having 4, 6, 8, 10, 12, 14, 16 and 20 faces...
, as each of the equilateral triangles can serve as faces, the edges of which adjoin isosceles triangles that can serve as tabs for gluing the model together.

