
Hexagonal tiling
Encyclopedia
In geometry
, the hexagonal tiling is a regular tiling of the Euclidean plane, in which three hexagons meet at each vertex. It has Schläfli symbol of {6,3} or t{3,6} (as a truncated triangular tiling).
Conway
calls it a hextille.
The internal angle of the hexagon is 120 degrees so three hexagons at a point make a full 360 degrees. It is one of three regular tilings of the plane. The other two are the triangular tiling and the square tiling.
in two dimensions. It also has the thinnest covering of any two-dimensional pattern, and is optimal in many other ways. For these reasons, the hexagonal pattern exists in nature in a beehive's honeycomb
. The optimal three-dimensional structure for making beehives (or rather, soap bubbles) was investigated by Lord Kelvin, who believed that the Kelvin structure (or body-centered cubic lattice) is optimal. However, the less regular Weaire-Phelan structure
is slightly better.
Chicken wire
consists of a hexagonal lattice of wires. This structure exists naturally in the form of graphite
, where each sheet of graphene
resembles chicken wire, with strong covalent carbon bonds. Tubular graphene sheets have been synthesised; these are known as carbon nanotube
s. They have many potential applications, due to their high tensile strength
and electrical properties.
The hexagonal tiling appears in many crystals. In three dimensions, the face-centered cubic and hexagonal close packing are common crystal structures. They are the densest known sphere packings in three dimensions, and are believed to be optimal. Structurally, they comprise parallel layers of hexagonal tilings, similar to the structure of graphite. They differ in the way that the layers are staggered from each other, with the face-centered cubic being the more regular of the two. Pure copper
, amongst other materials, forms a face-centered cubic lattice.
s of a hexagonal tiling, all generated from reflective symmetry of Wythoff construction
s.
The 3-color tiling is a tessellation generated by the order-3 permutohedron
s.
 The hexagonal tiling can be stretched and adjusted to other geometric proportions and different symmetries.
The hexagonal tiling can be stretched and adjusted to other geometric proportions and different symmetries.
The standard brick pattern can be considered a nonregular hexagonal tiling. Each rectangular brick has vertices inserted on the two long edges, dividing them into two collinear edges.
It can also be distorted into a chiral
4-colored tri-directional weaved pattern, distorting some hexagons into parallelogram
s. The weaved pattern with 4-colored faces have rotational 632 (p6) symmetry. The herringbone pattern
is also a distorted hexagonal tiling.
n3, as a part of sequence that continues into the hyperbolic plane
.
It is similarly related to the uniform truncated
polyhedra with vertex figure n.6.6.
This tiling is also a part of a sequence of truncated rhombic polyhedra and tilings with [n,3] Coxeter group
symmetry. The cube can be seen as a rhombic hexahedron where the rhombi are squares. The truncated forms have regular n-gons at the truncated vertices, and nonregular hexagonal faces. The sequence has two vertex figures (n.6.6) and (6,6,6).
The hexagonal tiling can be considered an elongated rhombic tiling, where each vertex of the rhombic tiling is stretched into a new edge. This is similar to the relation of the rhombic dodecahedron and the rhombo-hexagonal dodecahedron
tessellations in 3 dimensions.
there are eight uniform tiling
s that can be based from the regular hexagonal tiling (or the dual triangular tiling).
Drawing the tiles colored as red on the original faces, yellow at the original vertices, and blue along the original edges, there are 8 forms, 7 which are topologically distinct. (The truncated triangular tiling is topologically identical to the hexagonal tiling.)
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, the hexagonal tiling is a regular tiling of the Euclidean plane, in which three hexagons meet at each vertex. It has Schläfli symbol of {6,3} or t{3,6} (as a truncated triangular tiling).
Conway
John Horton Conway
John Horton Conway is a prolific mathematician active in the theory of finite groups, knot theory, number theory, combinatorial game theory and coding theory...
calls it a hextille.
The internal angle of the hexagon is 120 degrees so three hexagons at a point make a full 360 degrees. It is one of three regular tilings of the plane. The other two are the triangular tiling and the square tiling.
Applications
The hexagonal tiling is the densest way to arrange circlesSphere packing
In geometry, a sphere packing is an arrangement of non-overlapping spheres within a containing space. The spheres considered are usually all of identical size, and the space is usually three-dimensional Euclidean space...
in two dimensions. It also has the thinnest covering of any two-dimensional pattern, and is optimal in many other ways. For these reasons, the hexagonal pattern exists in nature in a beehive's honeycomb
Honeycomb
A honeycomb is a mass of hexagonal waxcells built by honey bees in their nests to contain their larvae and stores of honey and pollen.Beekeepers may remove the entire honeycomb to harvest honey...
. The optimal three-dimensional structure for making beehives (or rather, soap bubbles) was investigated by Lord Kelvin, who believed that the Kelvin structure (or body-centered cubic lattice) is optimal. However, the less regular Weaire-Phelan structure
Weaire-Phelan structure
In geometry, the Weaire–Phelan structure is a complex 3-dimensional structure representing an idealised foam of equal-sized bubbles. In 1993, Trinity College Dublin physicist Denis Weaire and his student Robert Phelan found that in computer simulations of foam, this structure was a better...
is slightly better.
Chicken wire
Chicken wire
Chicken wire, or poultry netting, is a mesh of wire commonly used to fence poultry livestock. It is made of thin, flexible galvanized wire, with hexagonal gaps...
consists of a hexagonal lattice of wires. This structure exists naturally in the form of graphite
Graphite
The mineral graphite is one of the allotropes of carbon. It was named by Abraham Gottlob Werner in 1789 from the Ancient Greek γράφω , "to draw/write", for its use in pencils, where it is commonly called lead . Unlike diamond , graphite is an electrical conductor, a semimetal...
, where each sheet of graphene
Graphene
Graphene is an allotrope of carbon, whose structure is one-atom-thick planar sheets of sp2-bonded carbon atoms that are densely packed in a honeycomb crystal lattice. The term graphene was coined as a combination of graphite and the suffix -ene by Hanns-Peter Boehm, who described single-layer...
resembles chicken wire, with strong covalent carbon bonds. Tubular graphene sheets have been synthesised; these are known as carbon nanotube
Carbon nanotube
Carbon nanotubes are allotropes of carbon with a cylindrical nanostructure. Nanotubes have been constructed with length-to-diameter ratio of up to 132,000,000:1, significantly larger than for any other material...
s. They have many potential applications, due to their high tensile strength
Tensile strength
Ultimate tensile strength , often shortened to tensile strength or ultimate strength, is the maximum stress that a material can withstand while being stretched or pulled before necking, which is when the specimen's cross-section starts to significantly contract...
and electrical properties.
The hexagonal tiling appears in many crystals. In three dimensions, the face-centered cubic and hexagonal close packing are common crystal structures. They are the densest known sphere packings in three dimensions, and are believed to be optimal. Structurally, they comprise parallel layers of hexagonal tilings, similar to the structure of graphite. They differ in the way that the layers are staggered from each other, with the face-centered cubic being the more regular of the two. Pure copper
Copper
Copper is a chemical element with the symbol Cu and atomic number 29. It is a ductile metal with very high thermal and electrical conductivity. Pure copper is soft and malleable; an exposed surface has a reddish-orange tarnish...
, amongst other materials, forms a face-centered cubic lattice.
Uniform colorings
There are 3 distinct uniform coloringUniform coloring
In geometry, a uniform coloring is a property of a uniform figure that is colored to be vertex-transitive...
s of a hexagonal tiling, all generated from reflective symmetry of Wythoff construction
Wythoff construction
In geometry, a Wythoff construction, named after mathematician Willem Abraham Wythoff, is a method for constructing a uniform polyhedron or plane tiling. It is often referred to as Wythoff's kaleidoscopic construction.- Construction process :...
s.
| k-uniform | 1-uniform | 2-uniform | |||
|---|---|---|---|---|---|
| Picture |  |
 |
 |
||
| Schläfli symbol | {6,3} | t{3,6} | t0,1,2{3[3]} | ||
| Wythoff symbol Wythoff symbol In geometry, the Wythoff symbol was first used by Coxeter, Longeut-Higgens and Miller in their enumeration of the uniform polyhedra. It represents a construction by way of Wythoff's construction applied to Schwarz triangles.... |
3 | 6 2 | 2 6 | 3 | 3 3 3 | | ||
| symmetry | *632 (p6m) | *632 (p6m) | *333 (p3) | *632 (p6m) | *632 (p6m) |
| Coxeter-Dynkin diagram Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... |
|||||
| Conway polyhedron notation Conway polyhedron notation Conway polyhedron notation is used to describe polyhedra based on a seed polyhedron modified by various operations.The seed polyhedra are the Platonic solids, represented by their first letter of their name ; the prisms , antiprisms and pyramids... |
H | tH | teH | t6daH | t6dateH |
The 3-color tiling is a tessellation generated by the order-3 permutohedron
Permutohedron
In mathematics, the permutohedron of order n is an -dimensional polytope embedded in an n-dimensional space, the vertices of which are formed by permuting the coordinates of the vector .-History:According to , permutohedra were first studied by...
s.
Topologically identical tilings

The standard brick pattern can be considered a nonregular hexagonal tiling. Each rectangular brick has vertices inserted on the two long edges, dividing them into two collinear edges.
It can also be distorted into a chiral
Chirality (mathematics)
In geometry, a figure is chiral if it is not identical to its mirror image, or, more precisely, if it cannot be mapped to its mirror image by rotations and translations alone. For example, a right shoe is different from a left shoe, and clockwise is different from counterclockwise.A chiral object...
4-colored tri-directional weaved pattern, distorting some hexagons into parallelogram
Parallelogram
In Euclidean geometry, a parallelogram is a convex quadrilateral with two pairs of parallel sides. The opposite or facing sides of a parallelogram are of equal length and the opposite angles of a parallelogram are of equal measure...
s. The weaved pattern with 4-colored faces have rotational 632 (p6) symmetry. The herringbone pattern
Herringbone pattern
The herringbone pattern is an arrangement of rectangles used for floor tilings and road pavement.The blocks can be rectangles or parallelograms...
is also a distorted hexagonal tiling.
| Regular hexagons | Hexagonal weave |
|---|---|
| p6m (*632) | p6 (632) |
 |
|
| Brick pattern | Herringbone |
| p4g (4*2) | |
Related polyhedra and tilings
This tiling is topologically related to regular polyhedra with vertex figureVertex figure
In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...
n3, as a part of sequence that continues into the hyperbolic plane
Hyperbolic space
In mathematics, hyperbolic space is a type of non-Euclidean geometry. Whereas spherical geometry has a constant positive curvature, hyperbolic geometry has a negative curvature: every point in hyperbolic space is a saddle point...
.
 (33 Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids... ) |
 (43 Cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and... ) |
 (53) |
 (63) tiling |
 (73) tiling |
It is similarly related to the uniform truncated
Truncation (geometry)
In geometry, a truncation is an operation in any dimension that cuts polytope vertices, creating a new facet in place of each vertex.- Uniform truncation :...
polyhedra with vertex figure n.6.6.
 (3.6.6) Truncated tetrahedron In geometry, the truncated tetrahedron is an Archimedean solid. It has 4 regular hexagonal faces, 4 regular triangular faces, 12 vertices and 18 edges.- Area and volume :... |
 (4.6.6) Truncated octahedron In geometry, the truncated octahedron is an Archimedean solid. It has 14 faces , 36 edges, and 24 vertices. Since each of its faces has point symmetry the truncated octahedron is a zonohedron.... |
 (5.6.6) Truncated icosahedron In geometry, the truncated icosahedron is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids whose faces are two or more types of regular polygons.It has 12 regular pentagonal faces, 20 regular hexagonal faces, 60 vertices and 90 edges.... |
 (6.6.6) tiling |
 (7.6.6) tiling Order-7 truncated triangular tiling In geometry, the Order 7 truncated heptagonal tiling, sometimes called the hyperbolic soccerball, is a semiregular tiling of the hyperbolic plane. There are two hexagons and one heptagon on each vertex, forming a pattern similar to a conventional soccer ball with heptagons in place of pentagons... |
This tiling is also a part of a sequence of truncated rhombic polyhedra and tilings with [n,3] Coxeter group
Coxeter group
In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example...
symmetry. The cube can be seen as a rhombic hexahedron where the rhombi are squares. The truncated forms have regular n-gons at the truncated vertices, and nonregular hexagonal faces. The sequence has two vertex figures (n.6.6) and (6,6,6).
| Polyhedra | Euclidean tiling | Hyperbolic tiling | |||
|---|---|---|---|---|---|
| [3,3] | [4,3] | [5,3] | [6,3] | [7,3] | [8,3] |
 Cube Cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and... |
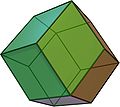 Rhombic dodecahedron Rhombic dodecahedron In geometry, the rhombic dodecahedron is a convex polyhedron with 12 rhombic faces. It is an Archimedean dual solid, or a Catalan solid. Its dual is the cuboctahedron.-Properties:... |
 Rhombic triacontahedron Rhombic triacontahedron In geometry, the rhombic triacontahedron is a convex polyhedron with 30 rhombic faces. It is an Archimedean dual solid, or a Catalan solid. It is the polyhedral dual of the icosidodecahedron, and it is a zonohedron.... |
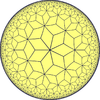
Rhombille |
 |
|
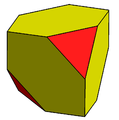 Alternate truncated cube |
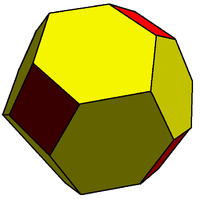 Truncated rhombic dodecahedron Truncated rhombic dodecahedron The truncated rhombic dodecahedron is a convex polyhedron constructed from the rhombic dodecahedron by truncating the 6 vertices.The 6 vertices are truncated such that all edges are equal length. The original 12 rhombic faces become flattened hexagons, and the truncated vertices become squares.The... |
 Truncated rhombic triacontahedron Truncated rhombic triacontahedron The truncated rhombic triacontahedron is a convex polyhedron constructed as a truncation of the rhombic triacontahedron. It can more accurately be called a pentatruncated rhombic triacontahedron because only the order-5 vertices are truncated.... |
Hexagonal tiling |
The hexagonal tiling can be considered an elongated rhombic tiling, where each vertex of the rhombic tiling is stretched into a new edge. This is similar to the relation of the rhombic dodecahedron and the rhombo-hexagonal dodecahedron
Rhombo-hexagonal dodecahedron
The rhombo-hexagonal dodecahedron is a convex polyhedron with 8 rhombic and 4 equilateral hexagonal faces.It is also called an elongated dodecahedron and extended rhombic dodecahedron because it is related to the rhombic dodecahedron by expanding four rhombic faces of the rhombic dodecahedron into...
tessellations in 3 dimensions.
 Rhombic tiling |
 Hexagonal tiling |
Fencing uses this relation |
Wythoff constructions from hexagonal and triangular tilings
Like the uniform polyhedraUniform polyhedron
A uniform polyhedron is a polyhedron which has regular polygons as faces and is vertex-transitive...
there are eight uniform tiling
Uniform tiling
In geometry, a uniform tiling is a tessellation of the plane by regular polygon faces with the restriction of being vertex-uniform.Uniform tilings can exist in both the Euclidean plane and hyperbolic plane...
s that can be based from the regular hexagonal tiling (or the dual triangular tiling).
Drawing the tiles colored as red on the original faces, yellow at the original vertices, and blue along the original edges, there are 8 forms, 7 which are topologically distinct. (The truncated triangular tiling is topologically identical to the hexagonal tiling.)
| Tiling | Schläfli symbol |
Wythoff symbol Wythoff construction In geometry, a Wythoff construction, named after mathematician Willem Abraham Wythoff, is a method for constructing a uniform polyhedron or plane tiling. It is often referred to as Wythoff's kaleidoscopic construction.- Construction process :... |
Vertex figure Vertex configuration In geometry, a vertex configuration is a short-hand notation for representing the vertex figure of a polyhedron or tiling as the sequence of faces around a vertex. For uniform polyhedra there is only one vertex type and therefore the vertex configuration fully defines the polyhedron... |
Image |
|---|---|---|---|---|
| Hexagonal tiling | t0{6,3} | 3 | 6 2 | 63 |  |
| Truncated hexagonal tiling Truncated hexagonal tiling In geometry, the truncated hexagonal tiling is a semiregular tiling of the Euclidean plane. There are 2 dodecagons and one triangle on each vertex.... |
t0,1{6,3} | 2 3 | 6 | 3.12.12 |  |
| Rectified hexagonal tiling (Trihexagonal tiling Trihexagonal tiling In geometry, the trihexagonal tiling is a semiregular tiling of the Euclidean plane. There are two triangles and two hexagons alternating on each vertex... ) |
t1{6,3} | 2 | 6 3 | (3.6)2 |  |
| Bitruncated hexagonal tiling (Truncated triangular tiling) |
t1,2{6,3} | 2 6 | 3 | 6.6.6 |  |
| Dual hexagonal tiling (Triangular tiling) |
t2{6,3} | 6 | 3 2 | 36 |  |
| Cantellated hexagonal tiling (Rhombitrihexagonal tiling) |
t0,2{6,3} | 6 3 | 2 | 3.4.6.4 |  |
| Omnitruncated hexagonal tiling (Truncated trihexagonal tiling) |
t0,1,2{6,3} | 6 3 2 | | 4.6.12 |  |
| Snub hexagonal tiling Snub hexagonal tiling In geometry, the Snub hexagonal tiling is a semiregular tiling of the Euclidean plane. There are four triangles and one hexagon on each vertex... |
s{6,3} | | 6 3 2 | 3.3.3.3.6 |  |
See also
- Hexagonal latticeHexagonal latticeThe hexagonal lattice or equilateral triangular lattice is one of the five 2D lattice types.Three nearby points form an equilateral triangle. In images four orientations of such a triangle are by far the most common...
- Hexagonal prismatic honeycombHexagonal prismatic honeycombThe hexagonal prismatic honeycomb is a space-filling tessellation in Euclidean 3-space made up of hexagonal prisms.It is constructed from a hexagonal tiling extruded into prisms.It is one of 28 convex uniform honeycombs.- References :...
- Tilings of regular polygons
- List of uniform tilings
- List of regular polytopes

