
Truncated icosahedron
Encyclopedia
In geometry
, the truncated icosahedron
is an Archimedean solid
, one of thirteen convex isogonal nonprismatic solids whose face
s are two or more types of regular polygons.
It has 12 regular pentagon
al faces, 20 regular hexagonal faces, 60 vertices and 90 edges.
with the 12 vertices truncated
(cut off) such that one third of each edge is cut off at each of both ends. This creates 12 new pentagon faces, and leaves the original 20 triangle faces as regular hexagons. Thus the length of the edges is one third of that of the original edges.
where φ = (1+√5)/2 is the golden mean
. Using φ2 = φ + 1 one verifies that all vertices are on a sphere, centered at the origin, with the radius squared equal to 9φ + 10. The edges have length 2.
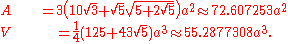
:
With unit edges, the surface area is (rounded) 21 for the pentagons and 52 for the hexagons, together 73 (see areas of regular polygons).

 The balls used in association football and team handball are perhaps the best-known example of a spherical polyhedron
The balls used in association football and team handball are perhaps the best-known example of a spherical polyhedron
analog to the truncated icosahedron, found in everyday life. The ball comprises the same pattern of regular pentagons and regular hexagons, but it is more spherical due to the pressure of the air inside and the elasticity of the ball. This ball type was introduced in 1970; starting with the 2006 World Cup, the design has been superseded by newer patterns.
A variation of the icosahedron was used as the basis of the honeycomb wheels (made from a polycast material) used by the Pontiac Motor Division between 1971 to 1976 on its Trans Am and Grand Prix.
This shape was also the configuration of the lenses used for focusing the explosive shock waves of the detonators in both the gadget and Fat Man
atomic bombs.
The truncated icosahedron can also be described as a model of the Buckminsterfullerene
(fullerene) (C60), or "buckyball," molecule, an allotrope of elemental carbon, discovered in 1985. The diameter of the soccer ball and the fullerene molecule are 22 cm and ca. 1 nm
, respectively, hence the size ratio is 220,000,000 : 1.
The truncated icosahedron is also hypothesized in geology
to be the driving force behind many tectonic fabrics on earth
. According to the theory, since the shape is the closest geometric analog to the shape of the earth, it can explain the trend of many different fracture and associated features in plate tectonic rifting and craton
shape.
illustrating The Divine Proportion.
These uniform star-polyhedra, and one icosahedral stellation have nonuniform truncated icosahedra convex hull
s:
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, the truncated icosahedron
Icosahedron
In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids....
is an Archimedean solid
Archimedean solid
In geometry an Archimedean solid is a highly symmetric, semi-regular convex polyhedron composed of two or more types of regular polygons meeting in identical vertices...
, one of thirteen convex isogonal nonprismatic solids whose face
Face (geometry)
In geometry, a face of a polyhedron is any of the polygons that make up its boundaries. For example, any of the squares that bound a cube is a face of the cube...
s are two or more types of regular polygons.
It has 12 regular pentagon
Pentagon
In geometry, a pentagon is any five-sided polygon. A pentagon may be simple or self-intersecting. The sum of the internal angles in a simple pentagon is 540°. A pentagram is an example of a self-intersecting pentagon.- Regular pentagons :In a regular pentagon, all sides are equal in length and...
al faces, 20 regular hexagonal faces, 60 vertices and 90 edges.
Construction
This polyhedron can be constructed from an icosahedronIcosahedron
In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids....
with the 12 vertices truncated
Truncation (geometry)
In geometry, a truncation is an operation in any dimension that cuts polytope vertices, creating a new facet in place of each vertex.- Uniform truncation :...
(cut off) such that one third of each edge is cut off at each of both ends. This creates 12 new pentagon faces, and leaves the original 20 triangle faces as regular hexagons. Thus the length of the edges is one third of that of the original edges.
 Icosahedron Icosahedron In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids.... |
Cartesian coordinates
Cartesian coordinates for the vertices of a truncated icosahedron centered at the origin are all even permutations of:,±φ),±2φ)where φ = (1+√5)/2 is the golden mean
Golden ratio
In mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989...
. Using φ2 = φ + 1 one verifies that all vertices are on a sphere, centered at the origin, with the radius squared equal to 9φ + 10. The edges have length 2.
Orthogonal projections
The truncated icosahedron has five special orthogonal projections, centered, on a vertex, on two types of edges, and two types of faces: hexagonal and pentagonal. The last two correspond to the A2 and H2 Coxeter planes.| Centered by | Vertex | Edge 5-6 |
Edge 6-6 |
Face Hexagon |
Face Pentagon |
|---|---|---|---|---|---|
| Image | |||||
| Projective symmetry |
[2] | [2] | [2] | [6] | [10] |
Area and volume
The area A and the volume V of the truncated icosahedron of edge length a are: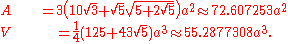
Geometric relations
The truncated icosahedron easily verifies the Euler characteristicEuler characteristic
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...
:
- 32 + 60 − 90 = 2.
With unit edges, the surface area is (rounded) 21 for the pentagons and 52 for the hexagons, together 73 (see areas of regular polygons).
Applications


Spherical polyhedron
In mathematics, a spherical polyhedron is a tiling of the sphere in which the surface is divided or partitioned by great arcs into bounded regions called spherical polygons...
analog to the truncated icosahedron, found in everyday life. The ball comprises the same pattern of regular pentagons and regular hexagons, but it is more spherical due to the pressure of the air inside and the elasticity of the ball. This ball type was introduced in 1970; starting with the 2006 World Cup, the design has been superseded by newer patterns.
A variation of the icosahedron was used as the basis of the honeycomb wheels (made from a polycast material) used by the Pontiac Motor Division between 1971 to 1976 on its Trans Am and Grand Prix.
This shape was also the configuration of the lenses used for focusing the explosive shock waves of the detonators in both the gadget and Fat Man
Fat Man
"Fat Man" is the codename for the atomic bomb that was detonated over Nagasaki, Japan, by the United States on August 9, 1945. It was the second of the only two nuclear weapons to be used in warfare to date , and its detonation caused the third man-made nuclear explosion. The name also refers more...
atomic bombs.
The truncated icosahedron can also be described as a model of the Buckminsterfullerene
Buckminsterfullerene
Buckminsterfullerene is a spherical fullerene molecule with the formula . It was first intentionally prepared in 1985 by Harold Kroto, James Heath, Sean O'Brien, Robert Curl and Richard Smalley at Rice University...
(fullerene) (C60), or "buckyball," molecule, an allotrope of elemental carbon, discovered in 1985. The diameter of the soccer ball and the fullerene molecule are 22 cm and ca. 1 nm
Nanometre
A nanometre is a unit of length in the metric system, equal to one billionth of a metre. The name combines the SI prefix nano- with the parent unit name metre .The nanometre is often used to express dimensions on the atomic scale: the diameter...
, respectively, hence the size ratio is 220,000,000 : 1.
The truncated icosahedron is also hypothesized in geology
Geology
Geology is the science comprising the study of solid Earth, the rocks of which it is composed, and the processes by which it evolves. Geology gives insight into the history of the Earth, as it provides the primary evidence for plate tectonics, the evolutionary history of life, and past climates...
to be the driving force behind many tectonic fabrics on earth
Earth
Earth is the third planet from the Sun, and the densest and fifth-largest of the eight planets in the Solar System. It is also the largest of the Solar System's four terrestrial planets...
. According to the theory, since the shape is the closest geometric analog to the shape of the earth, it can explain the trend of many different fracture and associated features in plate tectonic rifting and craton
Craton
A craton is an old and stable part of the continental lithosphere. Having often survived cycles of merging and rifting of continents, cratons are generally found in the interiors of tectonic plates. They are characteristically composed of ancient crystalline basement rock, which may be covered by...
shape.
Truncated icosahedra in the arts
A truncated icosahedron with "solid edges" is a drawing by Lucas PacioliLuca Pacioli
Fra Luca Bartolomeo de Pacioli was an Italian mathematician, Franciscan friar, collaborator with Leonardo da Vinci, and seminal contributor to the field now known as accounting...
illustrating The Divine Proportion.
Related polyhedra
| Picture |  Dodecahedron |
 Truncated dodecahedron Truncated dodecahedron In geometry, the truncated dodecahedron is an Archimedean solid. It has 12 regular decagonal faces, 20 regular triangular faces, 60 vertices and 90 edges.- Geometric relations :... |
 Icosidodecahedron Icosidodecahedron In geometry, an icosidodecahedron is a polyhedron with twenty triangular faces and twelve pentagonal faces. An icosidodecahedron has 30 identical vertices, with two triangles and two pentagons meeting at each, and 60 identical edges, each separating a triangle from a pentagon... |
 Truncated icosahedron Truncated icosahedron In geometry, the truncated icosahedron is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids whose faces are two or more types of regular polygons.It has 12 regular pentagonal faces, 20 regular hexagonal faces, 60 vertices and 90 edges.... |
 Icosahedron Icosahedron In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids.... |
|---|---|---|---|---|---|
| Coxeter-Dynkin Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... |
These uniform star-polyhedra, and one icosahedral stellation have nonuniform truncated icosahedra convex hull
Convex hull
In mathematics, the convex hull or convex envelope for a set of points X in a real vector space V is the minimal convex set containing X....
s:
 U73 Great rhombidodecahedron In geometry, the great rhombidodecahedron is a nonconvex uniform polyhedron, indexed as U73. Its vertex figure is a crossed quadrilateral.- Related polyhedra :... 2 5/3 (3/2 5/4) |
Complete stellation |
||
See also
- Spinning truncated icosahedron
- Dodecahedron
- IcosidodecahedronIcosidodecahedronIn geometry, an icosidodecahedron is a polyhedron with twenty triangular faces and twelve pentagonal faces. An icosidodecahedron has 30 identical vertices, with two triangles and two pentagons meeting at each, and 60 identical edges, each separating a triangle from a pentagon...
- Truncated dodecahedronTruncated dodecahedronIn geometry, the truncated dodecahedron is an Archimedean solid. It has 12 regular decagonal faces, 20 regular triangular faces, 60 vertices and 90 edges.- Geometric relations :...
- truncated rhombic triacontahedronTruncated rhombic triacontahedronThe truncated rhombic triacontahedron is a convex polyhedron constructed as a truncation of the rhombic triacontahedron. It can more accurately be called a pentatruncated rhombic triacontahedron because only the order-5 vertices are truncated....
- hyperbolic soccerball
- fullereneFullereneA fullerene is any molecule composed entirely of carbon, in the form of a hollow sphere, ellipsoid, or tube. Spherical fullerenes are also called buckyballs, and they resemble the balls used in association football. Cylindrical ones are called carbon nanotubes or buckytubes...
External links
- http://www.dr-mikes-math-games-for-kids.com/polyhedral-nets.html?net=FcWqcgCFwJy8hdr7Tpr0E5bZt5x3cWEH6dwwKHCmiAYTfaZwqWF0uEVMInwLYVXfN8PDwpUyauaLHhwJXg40Gas6xdXAY3rsGHjcD6k2QDzGzKkuLMI31aQ26rI3uD7eErma5wI9FxPhfb5HKttbwy3zq25bAOIRYmGDfrCf7sgmOwZShNBxNitreNFUEgEVyUztA9NGYxLLw6iOI3DGr1wAFohIvfYJ9v6CVDw7VE0C0NFaLQlslQ6L5acUJqQrPut6CxdTdxW1jRbZLXocrlCgQRpfanYeiaOBkYeHTpTQ1A5A8vkLNMrMDBl02ot2TMhJrhkI5ignSVOJ5X4S7GyUQMhdnriBZb447C6DLmqsGccUdj3C87AInlwfzYEQZvAXy0RR5QIt7WdIlLlcQldm&name=Truncated+Icosahedron#appletEditable printable net of a truncated icosahedron with interactive 3D view]
- The Uniform Polyhedra
- Virtual Reality Polyhedra The Encyclopedia of Polyhedra

