
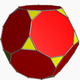
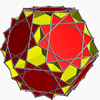
Truncated dodecahedron
Encyclopedia
In geometry
, the truncated dodecahedron is an Archimedean solid
. It has 12 regular decagon
al faces, 20 regular triangular
faces, 60 vertices and 90 edges.
can be formed from a dodecahedron by truncating
(cutting off) the corners so the pentagon
faces become decagon
s and the corners become triangle
s.
It is part of a truncation process between a dodecahedron and icosahedron:
It shares its vertex arrangement
with three nonconvex uniform polyhedra
:
It is used in the cell-transitive hyperbolic space-filling tessellation, the bitruncated icosahedral honeycomb.
V of a truncated dodecahedron of edge length a are: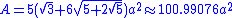
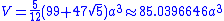
dodecahedron with edge length 2(τ-1), centered at the origin:
where τ = (1+√5)/2 is the golden ratio
(also written φ).
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, the truncated dodecahedron is an Archimedean solid
Archimedean solid
In geometry an Archimedean solid is a highly symmetric, semi-regular convex polyhedron composed of two or more types of regular polygons meeting in identical vertices...
. It has 12 regular decagon
Decagon
In geometry, a decagon is any polygon with ten sides and ten angles, and usually refers to a regular decagon, having all sides of equal length and each internal angle equal to 144°...
al faces, 20 regular triangular
Triangle
A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....
faces, 60 vertices and 90 edges.
Geometric relations
This polyhedronPolyhedron
In elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...
can be formed from a dodecahedron by truncating
Truncation (geometry)
In geometry, a truncation is an operation in any dimension that cuts polytope vertices, creating a new facet in place of each vertex.- Uniform truncation :...
(cutting off) the corners so the pentagon
Pentagon
In geometry, a pentagon is any five-sided polygon. A pentagon may be simple or self-intersecting. The sum of the internal angles in a simple pentagon is 540°. A pentagram is an example of a self-intersecting pentagon.- Regular pentagons :In a regular pentagon, all sides are equal in length and...
faces become decagon
Decagon
In geometry, a decagon is any polygon with ten sides and ten angles, and usually refers to a regular decagon, having all sides of equal length and each internal angle equal to 144°...
s and the corners become triangle
Triangle
A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....
s.
It is part of a truncation process between a dodecahedron and icosahedron:
| Picture |  Dodecahedron |
 Truncated dodecahedron Truncated dodecahedron In geometry, the truncated dodecahedron is an Archimedean solid. It has 12 regular decagonal faces, 20 regular triangular faces, 60 vertices and 90 edges.- Geometric relations :... |
 Icosidodecahedron Icosidodecahedron In geometry, an icosidodecahedron is a polyhedron with twenty triangular faces and twelve pentagonal faces. An icosidodecahedron has 30 identical vertices, with two triangles and two pentagons meeting at each, and 60 identical edges, each separating a triangle from a pentagon... |
 Truncated icosahedron Truncated icosahedron In geometry, the truncated icosahedron is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids whose faces are two or more types of regular polygons.It has 12 regular pentagonal faces, 20 regular hexagonal faces, 60 vertices and 90 edges.... |
 Icosahedron Icosahedron In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids.... |
|---|---|---|---|---|---|
| Coxeter-Dynkin Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... |
It shares its vertex arrangement
Vertex arrangement
In geometry, a vertex arrangement is a set of points in space described by their relative positions. They can be described by their use in polytopes....
with three nonconvex uniform polyhedra
Nonconvex uniform polyhedron
In geometry, a uniform star polyhedron is a self-intersecting uniform polyhedron. They are also sometimes called nonconvex polyhedra to imply self-intersecting...
:
 Truncated dodecahedron |
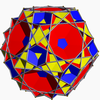 Great icosicosidodecahedron Great icosicosidodecahedron In geometry, the great icosicosidodecahedron is a nonconvex uniform polyhedron, indexed as U48. Its vertex figure is a crossed quadrilateral.- Related polyhedra :It shares its vertex arrangement with the truncated dodecahedron... |
 Great ditrigonal dodecicosidodecahedron Great ditrigonal dodecicosidodecahedron In geometry, the great ditrigonal dodecicosidodecahedron is a nonconvex uniform polyhedron, indexed as U42.- Related polyhedra :It shares its vertex arrangement with the truncated dodecahedron... |
 Great dodecicosahedron Great dodecicosahedron In geometry, the great dodecicosahedron is a nonconvex uniform polyhedron, indexed as U63. Its vertex figure is a crossed quadrilateral.It has a composite Wythoff symbol, 3 5/3 |, requiring two different Schwarz triangles to generate it: and .Its vertex figure 6.10/3.6/5.10/7 is also ambiguous,... |
It is used in the cell-transitive hyperbolic space-filling tessellation, the bitruncated icosahedral honeycomb.
Area and volume
The area A and the volumeVolume
Volume is the quantity of three-dimensional space enclosed by some closed boundary, for example, the space that a substance or shape occupies or contains....
V of a truncated dodecahedron of edge length a are:
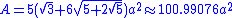
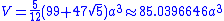
Cartesian coordinates
The following Cartesian coordinates define the vertices of a truncatedTruncation (geometry)
In geometry, a truncation is an operation in any dimension that cuts polytope vertices, creating a new facet in place of each vertex.- Uniform truncation :...
dodecahedron with edge length 2(τ-1), centered at the origin:
- (0, ±1/τ, ±(2+τ))
- (±(2+τ), 0, ±1/τ)
- (±1/τ, ±(2+τ), 0)
- (±1/τ, ±τ, ±2τ)
- (±2τ, ±1/τ, ±τ)
- (±τ, ±2τ, ±1/τ)
- (±τ, ±2, ±τ2)
- (±τ2, ±τ, ±2)
- (±2, ±τ2, ±τ)
where τ = (1+√5)/2 is the golden ratio
Golden ratio
In mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989...
(also written φ).
Orthogonal projections
The truncated dodecahedron has five special orthogonal projections, centered, on a vertex, on two types of edges, and two types of faces: hexagonal and pentagonal. The last two correspond to the A2 and H2 Coxeter planes.| Centered by | Vertex | Edge 3-10 |
Edge 10-10 |
Face Triangle |
Face Decagon |
|---|---|---|---|---|---|
| Image | |||||
| Projective symmetry |
[2] | [2] | [2] | [6] | [10] |
See also
- Spinning truncated dodecahedron
- icosahedronIcosahedronIn geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids....
- icosidodecahedronIcosidodecahedronIn geometry, an icosidodecahedron is a polyhedron with twenty triangular faces and twelve pentagonal faces. An icosidodecahedron has 30 identical vertices, with two triangles and two pentagons meeting at each, and 60 identical edges, each separating a triangle from a pentagon...
- truncated icosahedronTruncated icosahedronIn geometry, the truncated icosahedron is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids whose faces are two or more types of regular polygons.It has 12 regular pentagonal faces, 20 regular hexagonal faces, 60 vertices and 90 edges....
External links
- http://www.dr-mikes-math-games-for-kids.com/polyhedral-nets.html?net=1e9V3YL5nW2MMkIcdn0TdMHHhXMiuoCQGqz2g3IjH7orIJ5iBy9LQ80CKQP1GAP9MmtklgzVBcF5ZfK9LsPLcjTfCVtbQWJrpIJTarRzJGitPNEnHrk3rNm5pr6Gzui1P5MD7RwSrFu6TKzjy5qQl5PYokM9mcFWcoPivzjQxlRGa1eVpVmZl5Uv2nXTaX5RSgc2N5B3daPbsAUEsCGxrnbgMLCKvMvztIjl44GGTstwl3pC589OwhVUTHvkTzg6b4dpshGHQn4ajtxQA8chKkqzW1wKBsKuMpbqE4oCXbIi2sfEgppN1tcDBWVOJUXQfPiEglU1jtQi7fUj5xDW2PpZtdwQDmwpC3Lk&name=Truncated+Dodecahedron#appletEditable printable net of a truncated dodecahedron with interactive 3D view]
- The Uniform Polyhedra
- Virtual Reality Polyhedra The Encyclopedia of Polyhedra

