Spherical polyhedron - AbsoluteAstronomy.com

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, a spherical polyhedron is a tiling

Tessellation

A tessellation or tiling of the plane is a pattern of plane figures that fills the plane with no overlaps and no gaps. One may also speak of tessellations of parts of the plane or of other surfaces. Generalizations to higher dimensions are also possible. Tessellations frequently appeared in the art...

of the sphere

Sphere

A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...

in which the surface is divided or partitioned by great arcs into bounded regions called spherical polygons. Much of the theory of symmetrical polyhedra

Polyhedron

In elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...

is most conveniently derived in this way.

The most familiar spherical polyhedron is the soccer ball, thought of as a spherical truncated icosahedron.

Some polyhedra, such as the hosohedra and their duals

Dual polyhedron

In geometry, polyhedra are associated into pairs called duals, where the vertices of one correspond to the faces of the other. The dual of the dual is the original polyhedron. The dual of a polyhedron with equivalent vertices is one with equivalent faces, and of one with equivalent edges is another...

the dihedra
Dihedron
A dihedron is a type of polyhedron, made of two polygon faces which share the same set of edges. In three-dimensional Euclidean space, it is degenerate if its faces are flat, while in three-dimensional spherical space, a dihedron with flat faces can be thought of as a lens, an example of which is...

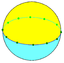
, exist as spherical polyhedra but have no flat-faced analogue. In the examples below, {2, 6} is a hosohedron and {6, 2} is the dual dihedron.

History

The first known man-made polyhedra are spherical polyhedra carved in stone. Many have been found in Scotland

Scotland

Scotland is a country that is part of the United Kingdom. Occupying the northern third of the island of Great Britain, it shares a border with England to the south and is bounded by the North Sea to the east, the Atlantic Ocean to the north and west, and the North Channel and Irish Sea to the...

, and appear to date from the neolithic

Neolithic

The Neolithic Age, Era, or Period, or New Stone Age, was a period in the development of human technology, beginning about 9500 BC in some parts of the Middle East, and later in other parts of the world. It is traditionally considered as the last part of the Stone Age...

period (the New Stone Age).

During the European "Dark Age", the Islamic scholar Abū al-Wafā' Būzjānī (Abu'l Wafa) wrote the first serious study of spherical polyhedra.

Two hundred years ago, at the start of the 19th Century, Poinsot

Louis Poinsot

Louis Poinsot was a French mathematician and physicist. Poinsot was the inventor of geometrical mechanics, showing how a system of forces acting on a rigid body could be resolved into a single force and a couple.-Life:...

used spherical polyhedra to discover the four regular star polyhedra.

In the middle of the 20th Century, Coxeter

Harold Scott MacDonald Coxeter

Harold Scott MacDonald "Donald" Coxeter, was a British-born Canadian geometer. Coxeter is regarded as one of the great geometers of the 20th century. He was born in London but spent most of his life in Canada....

used them to enumerate all but one of the uniform polyhedra

Uniform polyhedron

A uniform polyhedron is a polyhedron which has regular polygons as faces and is vertex-transitive...

, through the construction of kaleidoscopes (Wythoff construction

Wythoff construction

In geometry, a Wythoff construction, named after mathematician Willem Abraham Wythoff, is a method for constructing a uniform polyhedron or plane tiling. It is often referred to as Wythoff's kaleidoscopic construction.- Construction process :...

Examples

All the regular

Regular polyhedron

A regular polyhedron is a polyhedron whose faces are congruent regular polygons which are assembled in the same way around each vertex. A regular polyhedron is highly symmetrical, being all of edge-transitive, vertex-transitive and face-transitive - i.e. it is transitive on its flags...

and semiregular polyhedra

Semiregular polyhedron

The term semiregular polyhedron is used variously by different authors.In its original definition, it is a polyhedron with regular faces and a symmetry group which is transitive on its vertices, which is more commonly referred to today as a uniform polyhedron...

can be projected onto the sphere as tilings. Given by their Schläfli symbol {p, q} or vertex figure

Vertex figure

In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...

(a.b.c. ...):

(p q r)	{p,q}	(q.2p.2p)	(p.q.p.q)	(p. 2q.2q)	{q,p}	(q.4.p. 4)	(2r.2q.2p)	(3.r.3.q.3.p)
Tetrahedral (3 3 2)	{3,3} Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...	(3.6.6) Truncated tetrahedron In geometry, the truncated tetrahedron is an Archimedean solid. It has 4 regular hexagonal faces, 4 regular triangular faces, 12 vertices and 18 edges.- Area and volume :...	(3.3.3.3) Octahedron In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....	(3.6.6) Truncated tetrahedron In geometry, the truncated tetrahedron is an Archimedean solid. It has 4 regular hexagonal faces, 4 regular triangular faces, 12 vertices and 18 edges.- Area and volume :...	{3,3} Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...	(3.4.3.4) Cuboctahedron In geometry, a cuboctahedron is a polyhedron with eight triangular faces and six square faces. A cuboctahedron has 12 identical vertices, with two triangles and two squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such it is a quasiregular polyhedron,...	(4.6.6) Truncated octahedron In geometry, the truncated octahedron is an Archimedean solid. It has 14 faces , 36 edges, and 24 vertices. Since each of its faces has point symmetry the truncated octahedron is a zonohedron....	(3.2.3.3.3.3) Icosahedron In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids....
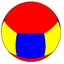
Octahedral (4 3 2)	{4,3} Cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and...	(3.8.8) Truncated cube In geometry, the truncated cube, or truncated hexahedron, is an Archimedean solid. It has 14 regular faces , 36 edges, and 24 vertices....	(3.4.3.4) Cuboctahedron In geometry, a cuboctahedron is a polyhedron with eight triangular faces and six square faces. A cuboctahedron has 12 identical vertices, with two triangles and two squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such it is a quasiregular polyhedron,...	(4.6.6) Truncated octahedron In geometry, the truncated octahedron is an Archimedean solid. It has 14 faces , 36 edges, and 24 vertices. Since each of its faces has point symmetry the truncated octahedron is a zonohedron....	{3,4} Octahedron In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....	(3.4.4.4)	(4.6.8)	(2.3.3.3.3.4) Snub cube In geometry, the snub cube, or snub cuboctahedron, is an Archimedean solid.The snub cube has 38 faces, 6 of which are squares and the other 32 are equilateral triangles. It has 60 edges and 24 vertices. It is a chiral polyhedron, that is, it has two distinct forms, which are mirror images of each...
Icosahedral (5 3 2)	{5,3}	(3.10.10) Truncated dodecahedron In geometry, the truncated dodecahedron is an Archimedean solid. It has 12 regular decagonal faces, 20 regular triangular faces, 60 vertices and 90 edges.- Geometric relations :...	(3.5.3.5) Icosidodecahedron In geometry, an icosidodecahedron is a polyhedron with twenty triangular faces and twelve pentagonal faces. An icosidodecahedron has 30 identical vertices, with two triangles and two pentagons meeting at each, and 60 identical edges, each separating a triangle from a pentagon...	(5.6.6) Truncated icosahedron In geometry, the truncated icosahedron is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids whose faces are two or more types of regular polygons.It has 12 regular pentagonal faces, 20 regular hexagonal faces, 60 vertices and 90 edges....	{3,5} Icosahedron In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids....	(3.4.5.4) Rhombicosidodecahedron In geometry, the rhombicosidodecahedron, or small rhombicosidodecahedron, is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids constructed of two or more types of regular polygon faces....	(4.6.10) Truncated icosidodecahedron In geometry, the truncated icosidodecahedron is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids constructed by two or more types of regular polygon faces....	(3.2.3.3.3.5) Snub dodecahedron In geometry, the snub dodecahedron, or snub icosidodecahedron, is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids constructed by two or more types of regular polygon faces....
Dihedral (6 2 2) example	{6,2} Dihedron A dihedron is a type of polyhedron, made of two polygon faces which share the same set of edges. In three-dimensional Euclidean space, it is degenerate if its faces are flat, while in three-dimensional spherical space, a dihedron with flat faces can be thought of as a lens, an example of which is...	(2.12.12) Dihedron A dihedron is a type of polyhedron, made of two polygon faces which share the same set of edges. In three-dimensional Euclidean space, it is degenerate if its faces are flat, while in three-dimensional spherical space, a dihedron with flat faces can be thought of as a lens, an example of which is...	(2.6.2.6) Dihedron A dihedron is a type of polyhedron, made of two polygon faces which share the same set of edges. In three-dimensional Euclidean space, it is degenerate if its faces are flat, while in three-dimensional spherical space, a dihedron with flat faces can be thought of as a lens, an example of which is...	(6.4.4) Hexagonal prism In geometry, the hexagonal prism is a prism with hexagonal base. The shape has 8 faces, 18 edges, and 12 vertices.Since it has eight faces, it is an octahedron. However, the term octahedron is primarily used to refer to the regular octahedron, which has eight triangular faces...	{2,6}	(2.4.6.4) Hexagonal prism In geometry, the hexagonal prism is a prism with hexagonal base. The shape has 8 faces, 18 edges, and 12 vertices.Since it has eight faces, it is an octahedron. However, the term octahedron is primarily used to refer to the regular octahedron, which has eight triangular faces...	(4.4.12) Dodecagonal prism In geometry, the dodecagonal prism is the tenth in an infinite set of prisms, formed by square sides and two regular dodecagon caps.If faces are all regular, it is a semiregular polyhedron.- Use :...	(3.2.3.2.3.6) Hexagonal antiprism In geometry, the hexagonal antiprism is the 4th in an infinite set of antiprisms formed by an even-numbered sequence of triangle sides closed by two polygon caps.If faces are all regular, it is a semiregular polyhedron.- See also :* Set of antiprisms...

Relation to tilings of the projective plane

Spherical polyhedra having at least one inversive symmetry are related to projective polyhedra (tessellations of the real projective plane

Real projective plane

In mathematics, the real projective plane is an example of a compact non-orientable two-dimensional manifold, that is, a one-sided surface. It cannot be embedded in our usual three-dimensional space without intersecting itself...

) – just as the sphere has a 2-to-1 covering map

Covering map

In mathematics, more specifically algebraic topology, a covering map is a continuous surjective function p from a topological space, C, to a topological space, X, such that each point in X has a neighbourhood evenly covered by p...

of the projective plane, projective polyhedra correspond under 2-fold cover to spherical polyhedra that are symmetric under reflection through the origin. For example, the 2-fold cover of the (projective) hemi-cube is the (spherical) cube.

History

Examples

Relation to tilings of the projective plane

See also