In geometry

Geometry

Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....

, a toroidal polyhedron is a polyhedron

Polyhedron

In elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...

 with a genus

Genus (mathematics)

In mathematics, genus has a few different, but closely related, meanings:-Orientable surface:The genus of a connected, orientable surface is an integer representing the maximum number of cuttings along non-intersecting closed simple curves without rendering the resultant manifold disconnected. It...

 of 1 or greater, representing topological torus

Torus

In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...

 surfaces.

Non-self-intersecting toroidal polyhedra are embedded

Embedding

In mathematics, an embedding is one instance of some mathematical structure contained within another instance, such as a group that is a subgroup....

 tori, while self-intersecting toroidal polyhedra are toroidal as abstract polyhedra, which can be verified by their Euler characteristic (0 or less) and orientability (orientable), and their self-intersecting realization in Euclidean 3-space is a polyhedral immersion.

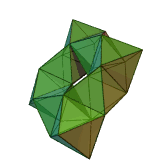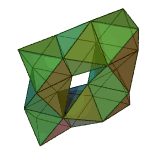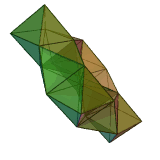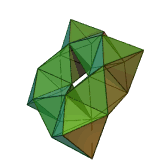
Stewart toroids

A special category of toroidal polyhedra are constructed exclusively by regular polygon

Regular polygon

A regular polygon is a polygon that is equiangular and equilateral . Regular polygons may be convex or star.-General properties:...

 faces, no intersections, and a further restriction that adjacent faces may not exist in the same plane. These are called Stewart toroids, named after Professor Bonnie Stewart

Bonnie Stewart

Bonnie Stewart was a professor of mathematics at Michigan State University from 1940 to 1980. In 1970 he published a book, Adventures among the toroids. A study of orientable polyhedra with regular faces, in which he discussed what are now called Stewart toroids...

 who explored their existence.

Stewart also defined them as quasi-convex toroidal polyhedra if the convex hull

Convex hull

In mathematics, the convex hull or convex envelope for a set of points X in a real vector space V is the minimal convex set containing X....

 created no new edges (i.e. the holes can be filled by single planar polygons).

Császár and Szilassi polyhedra

The Császár polyhedron

Császár polyhedron

In geometry, the Császár polyhedron is a nonconvex polyhedron, topologically a toroid, with 14 triangular faces.This polyhedron has no diagonals; every pair of vertices is connected by an edge. The seven vertices and 21 edges of the Császár polyhedron form an embedding of the complete graph K_7...

 is a seven-vertex toroidal polyhedron with 21 edges and 14 triangular faces. It and the tetrahedron

Tetrahedron

In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...

 are the only known polyhedra in which every possible line segment connecting two vertices forms an edge of the polyhedron. Its dual, the Szilassi polyhedron

Szilassi polyhedron

The Szilassi polyhedron is a nonconvex polyhedron, topologically a torus, with seven hexagonal faces.Each face of this polyhedron shares an edge with each other face. As a result, it requires seven colours to colour each adjacent face, providing the lower bound for the seven colour theorem...

, has seven hexagonal faces that are all adjacent to each other.

The Császár polyhedron has the fewest possible vertices of any toroidal polyhedron, and the Szilassi polyhedron has the fewest possible faces of any toroidal polyhedron.

Self-intersecting tori

Allowing faces to intersect produces toroidal polyhedra that are hard to see except by determining their Euler characteristic

Euler characteristic

In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...

: χ = 2(1 − g). Such polyhedra are toroidal as abstract polyhedra, and their self-intersecting realization in Euclidean 3-space is a polyhedral immersion.

For example:

• Genus 1:
  • Octahemioctahedron
    Octahemioctahedron
    In geometry, the octahemioctahedron is a nonconvex uniform polyhedron, indexed as U3. Its vertex figure is a crossed quadrilateral.It is one of nine hemipolyhedra with 4 hexagonal faces passing through the model center.- Related polyhedra :...
    
    
• Genus 3:
  • Small cubicuboctahedron
    Small cubicuboctahedron
    In geometry, the small cubicuboctahedron is a uniform star polyhedron, indexed as U13. It has 20 faces , 48 edges, and 24 vertices. Its vertex figure is a crossed quadrilateral.- Related polyhedra :...
    
    
• Genus 4:
  • Great dodecahedron

See also

• Johnson solid
  Johnson solid
  In geometry, a Johnson solid is a strictly convex polyhedron, each face of which is a regular polygon, but which is not uniform, i.e., not a Platonic solid, Archimedean solid, prism or antiprism. There is no requirement that each face must be the same polygon, or that the same polygons join around...
  
   – A similar set of convex polyhedra to the Stewart toroids
• Deltahedron
  Deltahedron
  A deltahedron is a polyhedron whose faces are all equilateral triangles. The name is taken from the Greek majuscule delta , which has the shape of an equilateral triangle. There are infinitely many deltahedra, but of these only eight are convex, having 4, 6, 8, 10, 12, 14, 16 and 20 faces...
  
   – Includes toroidal polyhedra with triangular faces
• Infinite skew polyhedron
  Infinite skew polyhedron
  In geometry, an infinite skew polyhedron is an extension of the idea of a polyhedron, consisting of regular polygon faces with nonplanar vertex figures, allowing the figure to extend indefinitely without folding round to form a closed surface....
  
  
• Spherical polyhedron
  Spherical polyhedron
  In mathematics, a spherical polyhedron is a tiling of the sphere in which the surface is divided or partitioned by great arcs into bounded regions called spherical polygons...
  
  
• Projective polyhedron
  Projective polyhedron
  In geometry, a projective polyhedron is a tessellation of the real projective plane. These are projective analogs of spherical polyhedra – tessellations of the sphere – and toroidal polyhedra – tessellations of the toroids....
  
  

External links

• Stewart Toroids (Toroidal Solids with Regular Polygon Faces)
• Stewart's polyhedra
• Toroidal Polyhedra
• Stewart toroids