
Infinite skew polyhedron
Encyclopedia
In geometry
, an infinite skew polyhedron is an extension of the idea of a polyhedron
, consisting of regular polygon
faces with nonplanar vertex figure
s, allowing the figure to extend indefinitely without folding round to form a closed surface.
Infinite skew polyhedra have also been called polyhedral sponges, and also hyperbolic tessellations because they can be seen as related to hyperbolic space
tessellations which also have negative angle defects
. They are examples of the more general class of infinite polyhedra, or apeirohedra
.
Many are directly related to a convex uniform honeycomb
, being the polygon
al surface of a honeycomb
with some of the cells
removed. Characteristically, an infinite skew polyhedron divides space into two halves. If one half is thought of as solid the figure is sometimes called a partial honeycomb.
Coxeter offered a modified Schläfli symbol {l,m|n} for these figures, with {l,m} implying the vertex figure
, m l-gons around a vertex, and n-gonal holes. Their vertex figures are skew polygon
s, zig-zagging between two planes.
The regular skew polyhedra, reresented by {l,m|n}, follow this equation:
Coxeter and Petrie found three of these that filled 3-space:
Beyond Euclidean 3-space, C. W. L. Garner determined a set of 32 regular skew polyhedra in hyperbolic 3-space, derived from the 4 regular hyperbolic honeycombs.
in 1967 published a larger set of seven infinite skew polyhedra which he called regular pseudopolyhedrons, including the three from Coxeter and four new ones.
Gott relaxed the definition of regularity to allow his new figures. Where Coxeter and Petrie had required that the vertices be symmetrical, Gott required only that they be congruent. Thus, Gott's new examples are not regular by Coxeter and Petrie's definition.
Gott called the full set of regular polyhedra, regular tilings, and regular pseudopolyhedrons as regular generalized polyhedra, representable by a {p,q} Schläfli symbol, with by p-gonal faces, q around each vertex.
A.F. Wells also published a list of pseudopolyhedra in the 1960s, including different forms with the same symbol: {4,5}, {3,7}, {3,8}, {3,10}, {3,12}.
However neither the term "pseudopolyhedron" nor Gott's definition of regularity have achieved wide usage.
There are two prismatic forms:
{5,5} is composed of 3 coplanar pentagon
s around a vertex and two perpendicular pentagons filling the gap.
Gott also acknowledged that there are other periodic forms of the regular planar tessellations. Both the square tiling {4,4} and triangular tiling {3,6} can be curved into approximating infinite cylinders in 3-space.
(vertex-transitive
) infinite skew polyhedra. Wachmann, Burt and Kleinmann (1974) discovered many examples but it is not known whether their list is complete.
Three are illustrated here:
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, an infinite skew polyhedron is an extension of the idea of a polyhedron
Polyhedron
In elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...
, consisting of regular polygon
Regular polygon
A regular polygon is a polygon that is equiangular and equilateral . Regular polygons may be convex or star.-General properties:...
faces with nonplanar vertex figure
Vertex figure
In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...
s, allowing the figure to extend indefinitely without folding round to form a closed surface.
Infinite skew polyhedra have also been called polyhedral sponges, and also hyperbolic tessellations because they can be seen as related to hyperbolic space
Hyperbolic space
In mathematics, hyperbolic space is a type of non-Euclidean geometry. Whereas spherical geometry has a constant positive curvature, hyperbolic geometry has a negative curvature: every point in hyperbolic space is a saddle point...
tessellations which also have negative angle defects
Defect (geometry)
In geometry, the defect means the failure of some angles to add up to the expected amount of 360° or 180°, when such angles in the plane would...
. They are examples of the more general class of infinite polyhedra, or apeirohedra
Apeirohedron
An apeirohedron is a polyhedron having infinitely many faces. Like an ordinary polyhedron it forms a surface with no border. But where an ordinary polyhedral surface has no border because it folds round to close back on itself, an apeirohedron has no border because its surface is unbounded.Two main...
.
Many are directly related to a convex uniform honeycomb
Convex uniform honeycomb
In geometry, a convex uniform honeycomb is a uniform tessellation which fills three-dimensional Euclidean space with non-overlapping convex uniform polyhedral cells.Twenty-eight such honeycombs exist:* the familiar cubic honeycomb and 7 truncations thereof;...
, being the polygon
Polygon
In geometry a polygon is a flat shape consisting of straight lines that are joined to form a closed chain orcircuit.A polygon is traditionally a plane figure that is bounded by a closed path, composed of a finite sequence of straight line segments...
al surface of a honeycomb
Honeycomb (geometry)
In geometry, a honeycomb is a space filling or close packing of polyhedral or higher-dimensional cells, so that there are no gaps. It is an example of the more general mathematical tiling or tessellation in any number of dimensions....
with some of the cells
Cell (geometry)
In geometry, a cell is a three-dimensional element that is part of a higher-dimensional object.- In polytopes :A cell is a three-dimensional polyhedron element that is part of the boundary of a higher-dimensional polytope, such as a polychoron or honeycomb For example, a cubic honeycomb is made...
removed. Characteristically, an infinite skew polyhedron divides space into two halves. If one half is thought of as solid the figure is sometimes called a partial honeycomb.
Regular skew polyhedra
According to Coxeter, in 1926 John Flinders Petrie generalized the concept of regular skew polygons (nonplanar polygons) to regular skew polyhedra.Coxeter offered a modified Schläfli symbol {l,m|n} for these figures, with {l,m} implying the vertex figure
Vertex figure
In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...
, m l-gons around a vertex, and n-gonal holes. Their vertex figures are skew polygon
Skew polygon
In geometry, a skew polygon is a polygon whose vertices do not lie in a plane. Skew polygons must have at least 4 vertices.A regular skew polygon is a skew polygon with equal edge lengths and which is vertex-transitive....
s, zig-zagging between two planes.
The regular skew polyhedra, reresented by {l,m|n}, follow this equation:
- 2*sin(π/l)*sin(π/m)=cos(π/n)
Coxeter and Petrie found three of these that filled 3-space:
| Regular skew polyhedra (partial) | ||
|---|---|---|
 {4,6|4} |
 {6,4|4} |
 {6,6|3} |
Beyond Euclidean 3-space, C. W. L. Garner determined a set of 32 regular skew polyhedra in hyperbolic 3-space, derived from the 4 regular hyperbolic honeycombs.
Gott's regular pseudopolyhedrons
J. Richard GottJ. Richard Gott
John Richard Gott III is a professor of astrophysical sciences at Princeton University. He is known for developing and advocating two cosmological theories with the flavor of science fiction: Time travel and the Doomsday argument.- Exotic matter time travel theories :Paul Davies's bestseller How...
in 1967 published a larger set of seven infinite skew polyhedra which he called regular pseudopolyhedrons, including the three from Coxeter and four new ones.
Gott relaxed the definition of regularity to allow his new figures. Where Coxeter and Petrie had required that the vertices be symmetrical, Gott required only that they be congruent. Thus, Gott's new examples are not regular by Coxeter and Petrie's definition.
Gott called the full set of regular polyhedra, regular tilings, and regular pseudopolyhedrons as regular generalized polyhedra, representable by a {p,q} Schläfli symbol, with by p-gonal faces, q around each vertex.
A.F. Wells also published a list of pseudopolyhedra in the 1960s, including different forms with the same symbol: {4,5}, {3,7}, {3,8}, {3,10}, {3,12}.
However neither the term "pseudopolyhedron" nor Gott's definition of regularity have achieved wide usage.
Prismatic forms
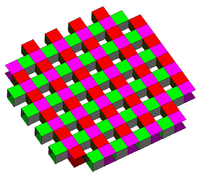 Prismatic form: {4,5} |
There are two prismatic forms:
- {4,5}: 5 squares on a vertex (Two parallel square tilings connected by cubicCubeIn geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and...
holes.) - {3,8}: 8 triangles on a vertex (Two parallel triangle tilings connected by octahedralOctahedronIn geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....
holes.)
Other forms
{3,10} is also formed from parallel planes of triangular tilings, with alternating octahedral holes going both ways.{5,5} is composed of 3 coplanar pentagon
Pentagon
In geometry, a pentagon is any five-sided polygon. A pentagon may be simple or self-intersecting. The sum of the internal angles in a simple pentagon is 540°. A pentagram is an example of a self-intersecting pentagon.- Regular pentagons :In a regular pentagon, all sides are equal in length and...
s around a vertex and two perpendicular pentagons filling the gap.
Gott also acknowledged that there are other periodic forms of the regular planar tessellations. Both the square tiling {4,4} and triangular tiling {3,6} can be curved into approximating infinite cylinders in 3-space.
Theorems
He wrote some theorems:- For every regular polyhedron {p,q}: (p-2)*(q-2)<4. For Every regular tessellation: (p-2)*(q-2)=4. For every regular pseudopolyhedron: (p-2)*(q-2)>4.
- The number of faces surrounding a given face is p*(q-2) in any regular generalized polyhedron.
- Every regular pseudopolyhedron approximates a negatively curved surface.
- The seven regular pseudopolyhedron are repeating structures.
Semiregular infinite skew polyhedra
There are many other semiregularSemiregular polyhedron
The term semiregular polyhedron is used variously by different authors.In its original definition, it is a polyhedron with regular faces and a symmetry group which is transitive on its vertices, which is more commonly referred to today as a uniform polyhedron...
(vertex-transitive
Vertex-transitive
In geometry, a polytope is isogonal or vertex-transitive if, loosely speaking, all its vertices are the same...
) infinite skew polyhedra. Wachmann, Burt and Kleinmann (1974) discovered many examples but it is not known whether their list is complete.
Three are illustrated here:
 A prismatic semiregular skew polyhedron with vertex configuration Vertex configuration In geometry, a vertex configuration is a short-hand notation for representing the vertex figure of a polyhedron or tiling as the sequence of faces around a vertex. For uniform polyhedra there is only one vertex type and therefore the vertex configuration fully defines the polyhedron... 4.4.4.6. |
A (partial) semiregular skew polyhedron with vertex configuration Vertex configuration In geometry, a vertex configuration is a short-hand notation for representing the vertex figure of a polyhedron or tiling as the sequence of faces around a vertex. For uniform polyhedra there is only one vertex type and therefore the vertex configuration fully defines the polyhedron... 4.8.4.8. Related to the omnitruncated cubic honeycomb Omnitruncated cubic honeycomb The omnitruncated cubic honeycomb is a uniform space-filling tessellation in Euclidean 3-space. It is composed of truncated cuboctahedra and octagonal prisms in a ratio of 1:3.A wireframe rendering- References :... . |
 A (partial) semiregular skew polyhedron with vertex configuration Vertex configuration In geometry, a vertex configuration is a short-hand notation for representing the vertex figure of a polyhedron or tiling as the sequence of faces around a vertex. For uniform polyhedra there is only one vertex type and therefore the vertex configuration fully defines the polyhedron... 3.4.4.4.4. Related to the Runcitruncated cubic honeycomb Runcitruncated cubic honeycomb The runcitruncated cubic honeycomb is a uniform space-filling tessellation in Euclidean 3-space. It is composed of small rhombicuboctahedra, truncated cubes, octagonal prisms, and cubes in a ratio of 1:1:3:3.... . |

