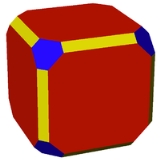
Vertex-transitive
Encyclopedia
Isogonal octagon (D4 symmetry) Blue and red lines of reflection are drawn |
|
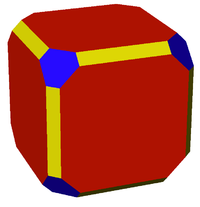 An isogonal truncated cuboctahedron Truncated cuboctahedron In geometry, the truncated cuboctahedron is an Archimedean solid. It has 12 square faces, 8 regular hexagonal faces, 6 regular octagonal faces, 48 vertices and 72 edges... , seen as cube Cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and... with its edges Edge (geometry) In geometry, an edge is a one-dimensional line segment joining two adjacent zero-dimensional vertices in a polygon. Thus applied, an edge is a connector for a one-dimensional line segment and two zero-dimensional objects.... bevel Bevel A beveled edge refers to an edge of a structure that is not perpendicular to the faces of the piece. The words bevel and chamfer overlap in usage; in general usage they are often interchanged, while in technical usage they may sometimes be differentiated as shown in the image at right.-Cutting... ed and its vertices Vertex (geometry) In geometry, a vertex is a special kind of point that describes the corners or intersections of geometric shapes.-Of an angle:... truncated Truncation (geometry) In geometry, a truncation is an operation in any dimension that cuts polytope vertices, creating a new facet in place of each vertex.- Uniform truncation :... . (Oh symmetry Octahedral symmetry 150px|thumb|right|The [[cube]] is the most common shape with octahedral symmetryA regular octahedron has 24 rotational symmetries, and a symmetry order of 48 including transformations that combine a reflection and a rotation... ) |
|
In geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, a polytope
Polytope
In elementary geometry, a polytope is a geometric object with flat sides, which exists in any general number of dimensions. A polygon is a polytope in two dimensions, a polyhedron in three dimensions, and so on in higher dimensions...
(a polygon
Polygon
In geometry a polygon is a flat shape consisting of straight lines that are joined to form a closed chain orcircuit.A polygon is traditionally a plane figure that is bounded by a closed path, composed of a finite sequence of straight line segments...
, polyhedron
Polyhedron
In elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...
or tiling, for example) is isogonal or vertex-transitive if, loosely speaking, all its vertices
Vertex (geometry)
In geometry, a vertex is a special kind of point that describes the corners or intersections of geometric shapes.-Of an angle:...
are the same. That implies that each vertex is surrounded by the same kinds of face
Face (geometry)
In geometry, a face of a polyhedron is any of the polygons that make up its boundaries. For example, any of the squares that bound a cube is a face of the cube...
in the same or reverse order, and with the same angles between corresponding faces.
Technically, we say that for any two vertices there exists a symmetry
Symmetry
Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...
of the polytope mapping the first isometrically
Isometry
In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
onto the second. Other ways of saying this are that the group of automorphisms of the polytope is transitive on its vertices, or that the vertices lie within a single symmetry orbit.
The term isogonal has long been used for polyhedra. Vertex-transitive is a synonym borrowed from modern ideas such as symmetry group
Symmetry group
The symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation...
s and graph theory
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
.
It is important to note that the pseudorhombicuboctahedron
Elongated square gyrobicupola
In geometry, the elongated square gyrobicupola or pseudorhombicuboctahedron is one of the Johnson solids . The 92 Johnson solids were named and described by Norman Johnson in 1966.- Relation to Rhombicuboctahedron :...
— which is 'not' isogonal — demonstrates that simply asserting that "all vertices look the same" is not as restrictive as the definition used here, which involves the group of isometries preserving the polyhedron or tiling.
2 dimensions: Isogonal polygons
All regular polygons and regular star polygons are isogonal.Some even-sided polygons which alternate two edge lengths, for example rectangle
Rectangle
In Euclidean plane geometry, a rectangle is any quadrilateral with four right angles. The term "oblong" is occasionally used to refer to a non-square rectangle...
, are isogonal.
All such 2n-gons have dihedral symmetry (Dn, n=2,3,...) with reflection lines across the mid-edge points.
3 dimensions: Isogonal polyhedra
Isogonal polyhedra may be classified:- RegularRegular polyhedronA regular polyhedron is a polyhedron whose faces are congruent regular polygons which are assembled in the same way around each vertex. A regular polyhedron is highly symmetrical, being all of edge-transitive, vertex-transitive and face-transitive - i.e. it is transitive on its flags...
if it is also isohedral (face-transitive) and isotoxal (edge-transitive); this implies that every face is the same kind of regular polygonRegular polygonA regular polygon is a polygon that is equiangular and equilateral . Regular polygons may be convex or star.-General properties:...
. - Quasi-regularQuasiregular polyhedronIn geometry, a quasiregular polyhedron is a semiregular polyhedron that has exactly two kinds of regular faces, which alternate around each vertex. They are edge-transitive and hence step closer to regularity than the semiregular which are merely vertex-transitive.There are only two convex...
if it is also isotoxal (edge-transitive) but not isohedral (face-transitive). - Semi-regularSemiregular polyhedronThe term semiregular polyhedron is used variously by different authors.In its original definition, it is a polyhedron with regular faces and a symmetry group which is transitive on its vertices, which is more commonly referred to today as a uniform polyhedron...
if every face is a regular polygon but it is not isohedral (face-transitive) or isotoxal (edge-transitive). (Definition varies among authors; e.g. some exclude solids with dihedral symmetry, or nonconvex solids.) - UniformUniform polyhedronA uniform polyhedron is a polyhedron which has regular polygons as faces and is vertex-transitive...
if every face is a regular polygon, i.e. it is regular, quasiregular or semi-regular. - NobleNoble polyhedronA noble polyhedron is one which is isohedral and isogonal . They were first studied in any depth by Hess and Bruckner around the turn of the century , and later by Grünbaum.-Classes of noble polyhedra:...
if it is also isohedral (face-transitive).
An isogonal polyhedron has a single kind of vertex figure
Vertex figure
In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...
. If the faces are regular (and the polyhedron is thus uniform) it can be represented by a vertex configuration
Vertex configuration
In geometry, a vertex configuration is a short-hand notation for representing the vertex figure of a polyhedron or tiling as the sequence of faces around a vertex. For uniform polyhedra there is only one vertex type and therefore the vertex configuration fully defines the polyhedron...
notation sequencing the faces around each vertex.
N dimensions: Isogonal polytopes and tessellations
These definitions can be extended to higher dimensional polytopePolytope
In elementary geometry, a polytope is a geometric object with flat sides, which exists in any general number of dimensions. A polygon is a polytope in two dimensions, a polyhedron in three dimensions, and so on in higher dimensions...
s and tessellations
Honeycomb (geometry)
In geometry, a honeycomb is a space filling or close packing of polyhedral or higher-dimensional cells, so that there are no gaps. It is an example of the more general mathematical tiling or tessellation in any number of dimensions....
. Most generally, all uniform polytope
Uniform polytope
A uniform polytope is a vertex-transitive polytope made from uniform polytope facets of a lower dimension. Uniform polytopes of 2 dimensions are the regular polygons....
s are isogonal, for example, the uniform polychoron
Uniform polychoron
In geometry, a uniform polychoron is a polychoron or 4-polytope which is vertex-transitive and whose cells are uniform polyhedra....
s and convex uniform honeycomb
Convex uniform honeycomb
In geometry, a convex uniform honeycomb is a uniform tessellation which fills three-dimensional Euclidean space with non-overlapping convex uniform polyhedral cells.Twenty-eight such honeycombs exist:* the familiar cubic honeycomb and 7 truncations thereof;...
s.
The dual of an isogonal polytope is called an isotope which is transitive on its facets.
k-isogonal figures
A polytope or tiling may be called k-isogonal if its vertices form k transitivity classes.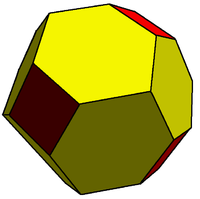 This truncated rhombic dodecahedron Truncated rhombic dodecahedron The truncated rhombic dodecahedron is a convex polyhedron constructed from the rhombic dodecahedron by truncating the 6 vertices.The 6 vertices are truncated such that all edges are equal length. The original 12 rhombic faces become flattened hexagons, and the truncated vertices become squares.The... is 2-isogonal because it contains two transitivity classes of vertices. This polyhedron is made of squares Square (geometry) In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles... and flattened hexagons. |
 This demiregular tiling is also 2-isogonal. This tiling is made of equilateral triangle, square and regular hexagonal faces. |
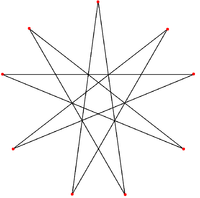 2-isogonal 9/4 enneagram Enneagram (geometry) In geometry, an enneagram is a nine-pointed geometric figure. It is sometimes called a nonagram.-Regular enneagram:A regular enneagram is constructed using the same points as the regular enneagon but connected in fixed steps... |
A more restrictive term, k-uniform figures is defined as an k-isogonal figure constructed only from regular polygon
Regular polygon
A regular polygon is a polygon that is equiangular and equilateral . Regular polygons may be convex or star.-General properties:...
s. They can be represented visually with colors by different uniform coloring
Uniform coloring
In geometry, a uniform coloring is a property of a uniform figure that is colored to be vertex-transitive...
s.
External links
- Isogonal Kaleidoscopical Polyhedra Vladimir L. Bulatov, Physics Department, Oregon State University, Corvallis, Presented at Mosaic2000, Millennial Open Symposium on the Arts and Interdisciplinary Computing, 21–24 August 2000, Seattle, WA
- Steven Dutch uses the term k-uniform for enumerating k-isogonal tilings
- List of n-uniform tilings (Also uses term k-uniform for k-isogonal)

