Uniform polytope
Encyclopedia
A uniform polytope is a vertex-transitive
polytope
made from uniform polytope facets
of a lower dimension. Uniform polytopes of 2 dimensions are the regular polygon
s.
This is a generalization of the older category of semiregular polytopes, but also includes the regular polytope
s. Further, nonconvex regular faces and vertex figure
s (star polygons) are allowed, which greatly expand the possible solutions. A strict definition requires uniform polytopes to be finite, while a more expansive definition allows uniform tessellation
s (tilings and honeycombs
) of Euclidean and hyperbolic space to be considered polytopes as well.
, and represented by a Coxeter-Dynkin diagram
. Notable exceptions include the grand antiprism
in four dimensions. The terminology for the convex uniform polytopes used in uniform polyhedron
, uniform polychoron
, uniform polyteron
, uniform polypeton, uniform tiling
, and convex uniform honeycomb
articles were coined by Norman Johnson.
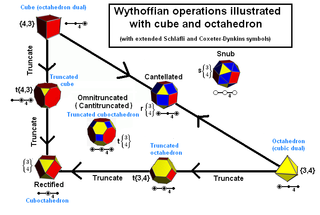
Equivalently, the Wythoffian polytopes can be generated by applying basic operations to the regular polytopes in that dimension. This approach was first used by Johannes Kepler
, and is the basis of the Conway polyhedron notation
.
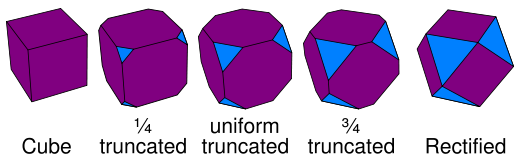
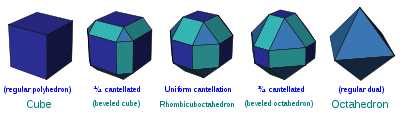
. The zeroth rectification is the original form. The (n−1)th rectification is the dual. The first rectification reduces edges to vertices. The second rectification reduces faces to vertices. The third rectification reduces cells to vertices, etc.
An extended Schläfli symbol can be used for representing rectified forms, with a single subscript:
In addition combinations of truncations can be performed which also generate new uniform polytopes. For example a cantitruncation is a cantellation and truncation applied together.
If all truncations are applied at once the operation can be more generally called an omnitruncation.
Names are given relative to the first ringed node, and Latin prefixes (used in the numeric powers
) is given to the position of the first ring. So for example, t1,2 is bitruncation, t2,3 is tritruncation, t3,4 is quadritruncation, etc.
The resulting polytopes always can be constructed, and are not generally reflective, and also do not in general have uniform polytope solutions.
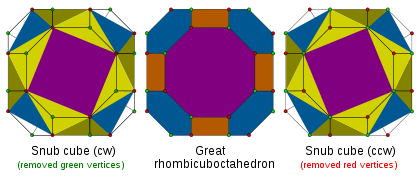
An alternation of a great rhombicuboctahedron produces a snub cube
.
The set of polytopes formed by alternating the hypercube
s are known as demicubes. In three dimensions, this produces a tetrahedron
; in four dimensions, this produces a 16-cell
, or demitesseract.
, the arrangement of edges, faces, cells, etc. around each vertex. Uniform polytopes represented by a Coxeter-Dynkin diagram
, marking active mirrors by rings, have reflectional symmetry, and can be simply constructed by recursive reflections of the vertex figure.
A smaller number of nonreflectional uniform polytopes have a single vertex figure but are not repeated by simple reflections. Most of these can be represented with operations like alternation of other uniform polytopes.
Vertex figures for single-ringed Coxeter-Dynkin diagram
s can be constructed from the diagram by removing the ringed node, and ringing neighboring nodes. Such vertex figures are themselves vertex-transitive.
Multiringed polytopes can be constructed by a slightly more complicated construction process, and their topology is not a uniform polytope. For example, the vertex figure of a truncated
regular polytope (with 2 rings) is a pyramid. An omnitruncated polytope (all nodes ringed) will always have an irregular simplex
as its vertex figure.
Uniform polytopes whose circumradius is equal to the edge length can be used as vertex figure
s for uniform tessellation
s. For example, the regular hexagon divides into 6 equilateral triangles and is the vertex figure for the regular triangular tiling. Also the cuboctahedron
divides into 8 regular tetrahedra and 6 square pyramids (half octahedron
), and it is the vertex figure for the alternated cubic honeycomb.
and hyperbolic space
are also considered to be (n+1)-dimensional. Hence, the tilings of two-dimensional space are grouped with the three-dimensional solids.
s, the simplest being the equilateral triangle
. The first few regular polygons are displayed below:
There is also an infinite set of star polygons (one for each rational number
greater than 2), but these are non-convex. The simplest example is the pentagram
, which corresponds to the rational number 5/2.
Regular polygons, represented by Schläfli symbol {p} for a p-gon. Regular polygons are self-dual, so the rectification produces the same polygon. The uniform truncation operation doubles the sides to {2p}. The snub operation, alternating the truncation, restores the original polygon {p}. Thus all uniform polygons are also regular. The following operations can be performed on regular polygons to derive the uniform polygons:
s:
In addition to these, there are also 13 semiregular polyhedra, or Archimedean solid
s, which can be obtained via Wythoff construction
s, or by performing operations such as truncation
on the Platonic solids, as demonstrated in the following table:
There is also the infinite set of prisms
, one for each regular polygon, and a corresponding set of antiprism
s.
The nonconvex uniform polyhedra include a further 4 regular polyhedra, the Kepler-Poinsot polyhedra, and 53 semiregular nonconvex polyhedra. There are also two infinite sets, the star prisms (one for each star polygon) and star antiprisms (one for each rational number greater than 3/2).
, which specifies the fundamental region of the object. An extension of Schläfli notation, also used by Coxeter
, applies to all dimensions; it consists of the letter 't', followed by a series of subscripted numbers corresponding to the ringed nodes of the Coxeter-Dynkin diagram
, and followed by the Schläfli symbol of the regular seed polytope. For example, the truncated octahedron
is represented by the notation: t0,1{3,4}.
), and two infinite sets: the prisms on the convex antiprisms, and the duoprism
s. There are also 41 convex semiregular polychora, including the non-Wythoffian grand antiprism
and the snub 24-cell
. Both of these special polychora are composed of subgroups of the vertices of the 600-cell.
The four-dimensional nonconvex uniform polytopes have not all been enumerated. The ones that have include the 10 regular nonconvex polychora (Schläfli-Hess polychora) and 57 prisms on the nonconvex uniform polyhedra, as well as three infinite families: the prisms on the star antiprisms, the duoprisms formed by multiplying
two star polygons, and the duoprisms formed by multiplying an ordinary polygon with a star polygon. There is an unknown number of polychora that do not fit into the above categories; over one thousand have been discovered so far.
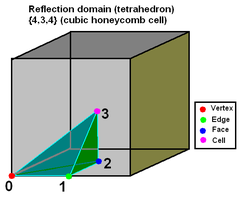
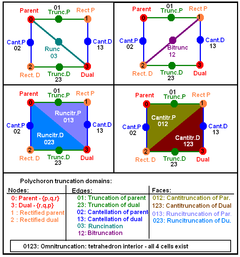Every regular polytope can be seen as the images of a fundamental region in a small number of mirrors. In a 4-dimensional polytope (or 3-dimensional cubic honeycomb) the fundamental region is bounded by four mirrors. A mirror in 4-space is a three-dimensional hyperplane
, but it is more convenient for our purposes to consider only its two-dimensional intersection with the three-dimensional surface of the hypersphere
; thus the mirrors form an irregular tetrahedron
.
Each of the sixteen regular polychora is generated by one of four symmetry groups, as follows:
(The groups are named in Coxeter
notation.)
Eight of the convex uniform honeycomb
s in Euclidean 3-space are analogously generated from the cubic honeycomb
{4,3,4}, by applying the same operations used to generate the Wythoffian uniform polychora.
For a given symmetry simplex, a generating point may be placed on any of the four vertices, 6 edges, 4 faces, or the interior volume. On each of these 15 elements there is a point whose images, reflected in the four mirrors, are the vertices of a uniform polychoron.
The extended Schläfli symbols are made by a t followed by inclusion of one to four subscripts 0,1,2,3. If there's one subscript, the generating point is on a corner of the fundamental region, i.e. a point where three mirrors meet. These corners are notated as
(For the two self-dual polychora, "dual" means a similar polychoron in dual position.) Two or more subscripts mean that the generating point is between the corners indicated.
s. The final 10th row lists the snub 24-cell constructions. This includes all nonprismatic uniform polychora, except for the non-Wythoffian grand antiprism
, which has no Coxeter family.
, simplex
and cross-polytope
. They are generalisations of the three-dimensional cube, tetrahedron and octahedron, respectively. There are no regular star polytopes in these dimensions. Most uniform higher-dimensional polytopes are obtained by modifying the regular polytopes, or by taking the Cartesian product of polytopes of lower dimensions.
In six, seven and eight dimensions, the exceptional
simple Lie group
s, E6, E7 and E8
come into play. By placing rings on a nonzero number of nodes of the Coxeter-Dynkin diagram
s, one can obtain 63 new 6-polytopes, 127 new 7-polytopes and 255 new 8-polytopes. A notable example is the Gosset 421 polytope
.
There are two classes of hyperbolic Coxeter groups, compact and noncompact. Uniform honeycombs generated by compact groups have finite facets and vertex figures, and exist from 2 to 4 dimensions. Noncompact groups have affine or hyperbolic subgraphs, and infinite facets or vertex figures, and exist from 3 to 10 dimensions.
Vertex-transitive
In geometry, a polytope is isogonal or vertex-transitive if, loosely speaking, all its vertices are the same...
polytope
Polytope
In elementary geometry, a polytope is a geometric object with flat sides, which exists in any general number of dimensions. A polygon is a polytope in two dimensions, a polyhedron in three dimensions, and so on in higher dimensions...
made from uniform polytope facets
Facet (mathematics)
A facet of a simplicial complex is a maximal simplex.In the general theory of polyhedra and polytopes, two conflicting meanings are currently jostling for acceptability:...
of a lower dimension. Uniform polytopes of 2 dimensions are the regular polygon
Regular polygon
A regular polygon is a polygon that is equiangular and equilateral . Regular polygons may be convex or star.-General properties:...
s.
This is a generalization of the older category of semiregular polytopes, but also includes the regular polytope
Regular polytope
In mathematics, a regular polytope is a polytope whose symmetry is transitive on its flags, thus giving it the highest degree of symmetry. All its elements or j-faces — cells, faces and so on — are also transitive on the symmetries of the polytope, and are regular polytopes of...
s. Further, nonconvex regular faces and vertex figure
Vertex figure
In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...
s (star polygons) are allowed, which greatly expand the possible solutions. A strict definition requires uniform polytopes to be finite, while a more expansive definition allows uniform tessellation
Uniform tessellation
In geometry, a uniform tessellation is a vertex-transitive tessellations made from uniform polytope facets. All of its vertices are identical and there is the same combination and arrangement of faces at each vertex....
s (tilings and honeycombs
Honeycomb (geometry)
In geometry, a honeycomb is a space filling or close packing of polyhedral or higher-dimensional cells, so that there are no gaps. It is an example of the more general mathematical tiling or tessellation in any number of dimensions....
) of Euclidean and hyperbolic space to be considered polytopes as well.
Operations
Nearly every uniform polytope can be generated by a Wythoff constructionWythoff construction
In geometry, a Wythoff construction, named after mathematician Willem Abraham Wythoff, is a method for constructing a uniform polyhedron or plane tiling. It is often referred to as Wythoff's kaleidoscopic construction.- Construction process :...
, and represented by a Coxeter-Dynkin diagram
Coxeter-Dynkin diagram
In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors...
. Notable exceptions include the grand antiprism
Grand antiprism
In geometry, the grand antiprism or pentagonal double antiprismoid is a uniform polychoron bounded by 320 cells: 20 pentagonal antiprisms, and 300 tetrahedra. It is an anomalous, non-Wythoffian uniform polychoron, discovered in 1965 by Conway and Guy.- Alternate names :* Pentagonal double...
in four dimensions. The terminology for the convex uniform polytopes used in uniform polyhedron
Uniform polyhedron
A uniform polyhedron is a polyhedron which has regular polygons as faces and is vertex-transitive...
, uniform polychoron
Uniform polychoron
In geometry, a uniform polychoron is a polychoron or 4-polytope which is vertex-transitive and whose cells are uniform polyhedra....
, uniform polyteron
Uniform polyteron
In geometry, a uniform polyteron is a five-dimensional uniform polytope. By definition, a uniform polyteron is vertex-transitive and constructed from uniform polychoron facets....
, uniform polypeton, uniform tiling
Uniform tiling
In geometry, a uniform tiling is a tessellation of the plane by regular polygon faces with the restriction of being vertex-uniform.Uniform tilings can exist in both the Euclidean plane and hyperbolic plane...
, and convex uniform honeycomb
Convex uniform honeycomb
In geometry, a convex uniform honeycomb is a uniform tessellation which fills three-dimensional Euclidean space with non-overlapping convex uniform polyhedral cells.Twenty-eight such honeycombs exist:* the familiar cubic honeycomb and 7 truncations thereof;...
articles were coined by Norman Johnson.
Equivalently, the Wythoffian polytopes can be generated by applying basic operations to the regular polytopes in that dimension. This approach was first used by Johannes Kepler
Johannes Kepler
Johannes Kepler was a German mathematician, astronomer and astrologer. A key figure in the 17th century scientific revolution, he is best known for his eponymous laws of planetary motion, codified by later astronomers, based on his works Astronomia nova, Harmonices Mundi, and Epitome of Copernican...
, and is the basis of the Conway polyhedron notation
Conway polyhedron notation
Conway polyhedron notation is used to describe polyhedra based on a seed polyhedron modified by various operations.The seed polyhedra are the Platonic solids, represented by their first letter of their name ; the prisms , antiprisms and pyramids...
.
Rectification operators
Regular n-polytopes have n orders of rectificationRectification (geometry)
In Euclidean geometry, rectification is the process of truncating a polytope by marking the midpoints of all its edges, and cutting off its vertices at those points...
. The zeroth rectification is the original form. The (n−1)th rectification is the dual. The first rectification reduces edges to vertices. The second rectification reduces faces to vertices. The third rectification reduces cells to vertices, etc.
An extended Schläfli symbol can be used for representing rectified forms, with a single subscript:
- k-th rectification = tk{p1, p2, ..., pn-1}
Truncation operators
Truncation operations that can be applied to regular n-polytopes in any combination. The resulting Coxeter-Dynkin diagram has two ringed nodes, and the operation is named for the distance between them. Truncation cuts vertices, cantellation cut edges, runcination cuts faces, sterication cut cells. Each higher operation also cuts lower ones too, so a cantellation also truncates vertices.- t0,1: TruncationTruncation (geometry)In geometry, a truncation is an operation in any dimension that cuts polytope vertices, creating a new facet in place of each vertex.- Uniform truncation :...
- applied to polygonPolygonIn geometry a polygon is a flat shape consisting of straight lines that are joined to form a closed chain orcircuit.A polygon is traditionally a plane figure that is bounded by a closed path, composed of a finite sequence of straight line segments...
s and higher. A truncation removes vertices, and inserts a new facet in place of each former vertex. Faces are truncated, doubling their edges. (The term, coined by Kepler, comes from Latin truncare 'to cut off'.) -
- t0,2: CantellationCantellation (geometry)In geometry, a cantellation is an operation in any dimension that cuts a regular polytope at its edges and vertices, creating a new facet in place of each edge and vertex. The operation also applies to regular tilings and honeycombs...
- applied to polyhedraUniform polyhedronA uniform polyhedron is a polyhedron which has regular polygons as faces and is vertex-transitive...
and higher. A cantellation truncates both vertices and edges and replaces them with new facets. Cells are replaced by topologically expandedExpansion (geometry)In geometry, expansion is a polytope operation where facets are separated and moved radially apart, and new facets are formed at separated elements...
copies of themselves. (The term, coined by Johnson, is derived from the verb cant, like bevelBevelA beveled edge refers to an edge of a structure that is not perpendicular to the faces of the piece. The words bevel and chamfer overlap in usage; in general usage they are often interchanged, while in technical usage they may sometimes be differentiated as shown in the image at right.-Cutting...
, meaning to cut with a slanted face.) -
- t0,3: RuncinationRuncinationIn geometry, runcination is an operation that cuts a regular polytope simultaneously along the faces, edges and vertices, creating new facets in place of the original face, edge, and vertex centers....
- applied to polychoraUniform polychoronIn geometry, a uniform polychoron is a polychoron or 4-polytope which is vertex-transitive and whose cells are uniform polyhedra....
and higher. Runcination truncates vertices, edges, and faces, replacing them each with new facets. 4-faces are replaced by topologically expanded copies of themselves. (The term, coined by Johnson, is derived from Latin runcina 'carpenter's planePlane (tool)A hand plane is a tool for shaping wood. When powered by electricity, the tool may be called a planer. Planes are used to flatten, reduce the thickness of, and impart a smooth surface to a rough piece of lumber or timber. Planing is used to produce horizontal, vertical, or inclined flat surfaces on...
'.) - t0,4: Sterication - applied to 5-polytopesUniform polyteronIn geometry, a uniform polyteron is a five-dimensional uniform polytope. By definition, a uniform polyteron is vertex-transitive and constructed from uniform polychoron facets....
and higher. Sterication truncates vertices, edges, faces, and cells, replacing each with new facets. 5-faces are replaced by topologically expanded copies of themselves. (The term, coined by Johnson, is derived from Greek stereos 'solid'.) - t0,5: Pentellation - applied to 6-polytopes and higher. Pentellation truncates vertices, edges, faces, cells, and 4-faces, replacing each with new facets. 6-faces are replaced by topologically expanded copies of themselves. (Pentellation is derived from Greek pente 'five'.)
- t0,6: Hexication - applied to 7-polytopes and higher. Hexication truncates vertices, edges, faces, cells, 4-faces, and 5-faces, replacing each with new facets. 7-faces are replaced by topologically expanded copies of themselves. (Hexication is derived from Greek hex 'six'.)
- t0,7: Heptellation - applied to 8-polytopes and higher. Heptellation truncates vertices, edges, faces, cells, 4-faces, 5-faces, and 6-faces, replacing each with new facets. 7-faces are replaced by topologically expanded copies of themselves. (Heptellation is derived from Greek hepta 'seven'.)
In addition combinations of truncations can be performed which also generate new uniform polytopes. For example a cantitruncation is a cantellation and truncation applied together.
If all truncations are applied at once the operation can be more generally called an omnitruncation.
Names are given relative to the first ringed node, and Latin prefixes (used in the numeric powers
Names of large numbers
This article lists and discusses the usage and derivation of names of large numbers, together with their possible extensions.The following table lists those names of large numbers which are found in many English dictionaries and thus have a special claim to being "real words"...
) is given to the position of the first ring. So for example, t1,2 is bitruncation, t2,3 is tritruncation, t3,4 is quadritruncation, etc.
Alternation
One special operation, called alternation, removes alternate vertices from a polytope with only even-sided faces. An alternated omnitruncated polytope is called a snub.The resulting polytopes always can be constructed, and are not generally reflective, and also do not in general have uniform polytope solutions.
An alternation of a great rhombicuboctahedron produces a snub cube
Snub cube
In geometry, the snub cube, or snub cuboctahedron, is an Archimedean solid.The snub cube has 38 faces, 6 of which are squares and the other 32 are equilateral triangles. It has 60 edges and 24 vertices. It is a chiral polyhedron, that is, it has two distinct forms, which are mirror images of each...
.
The set of polytopes formed by alternating the hypercube
Hypercube
In geometry, a hypercube is an n-dimensional analogue of a square and a cube . It is a closed, compact, convex figure whose 1-skeleton consists of groups of opposite parallel line segments aligned in each of the space's dimensions, perpendicular to each other and of the same length.An...
s are known as demicubes. In three dimensions, this produces a tetrahedron
Tetrahedron
In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...
; in four dimensions, this produces a 16-cell
16-cell
In four dimensional geometry, a 16-cell or hexadecachoron is a regular convex 4-polytope. It is one of the six regular convex 4-polytopes first described by the Swiss mathematician Ludwig Schläfli in the mid-19th century....
, or demitesseract.
Vertex figure
Uniform polytopes can be constructed from their vertex figureVertex figure
In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...
, the arrangement of edges, faces, cells, etc. around each vertex. Uniform polytopes represented by a Coxeter-Dynkin diagram
Coxeter-Dynkin diagram
In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors...
, marking active mirrors by rings, have reflectional symmetry, and can be simply constructed by recursive reflections of the vertex figure.
A smaller number of nonreflectional uniform polytopes have a single vertex figure but are not repeated by simple reflections. Most of these can be represented with operations like alternation of other uniform polytopes.
Vertex figures for single-ringed Coxeter-Dynkin diagram
Coxeter-Dynkin diagram
In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors...
s can be constructed from the diagram by removing the ringed node, and ringing neighboring nodes. Such vertex figures are themselves vertex-transitive.
Multiringed polytopes can be constructed by a slightly more complicated construction process, and their topology is not a uniform polytope. For example, the vertex figure of a truncated
Truncation (geometry)
In geometry, a truncation is an operation in any dimension that cuts polytope vertices, creating a new facet in place of each vertex.- Uniform truncation :...
regular polytope (with 2 rings) is a pyramid. An omnitruncated polytope (all nodes ringed) will always have an irregular simplex
Simplex
In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...
as its vertex figure.
Circumradius
Uniform polytopes have equal edge-lengths, and all vertices are an equal distance from the center, called the circumradius.Uniform polytopes whose circumradius is equal to the edge length can be used as vertex figure
Vertex figure
In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...
s for uniform tessellation
Uniform tessellation
In geometry, a uniform tessellation is a vertex-transitive tessellations made from uniform polytope facets. All of its vertices are identical and there is the same combination and arrangement of faces at each vertex....
s. For example, the regular hexagon divides into 6 equilateral triangles and is the vertex figure for the regular triangular tiling. Also the cuboctahedron
Cuboctahedron
In geometry, a cuboctahedron is a polyhedron with eight triangular faces and six square faces. A cuboctahedron has 12 identical vertices, with two triangles and two squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such it is a quasiregular polyhedron,...
divides into 8 regular tetrahedra and 6 square pyramids (half octahedron
Octahedron
In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....
), and it is the vertex figure for the alternated cubic honeycomb.
Uniform polytopes by dimension
It is useful to classify the uniform polytopes by dimension. This is equivalent to the number of nodes on the Coxeter-Dynkin diagram, or the number of hyperplanes in the Wythoffian construction. Because (n+1)-dimensional polytopes are tilings of n-dimensional spherical space, tilings of n-dimensional EuclideanEuclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
and hyperbolic space
Hyperbolic space
In mathematics, hyperbolic space is a type of non-Euclidean geometry. Whereas spherical geometry has a constant positive curvature, hyperbolic geometry has a negative curvature: every point in hyperbolic space is a saddle point...
are also considered to be (n+1)-dimensional. Hence, the tilings of two-dimensional space are grouped with the three-dimensional solids.
One dimension
The only one-dimensional polytope is the line segment. It corresponds to the Coxeter family A1.Two dimensions
In two dimensions, there is an infinite family of convex uniform polytopes, the regular polygonRegular polygon
A regular polygon is a polygon that is equiangular and equilateral . Regular polygons may be convex or star.-General properties:...
s, the simplest being the equilateral triangle
Triangle
A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....
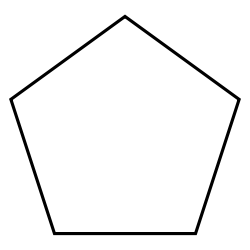
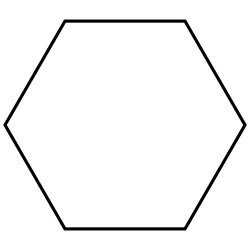
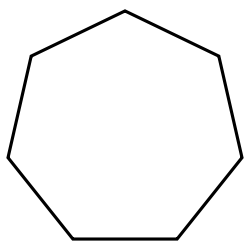
. The first few regular polygons are displayed below:
| Name | Triangle (2-simplex Simplex In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,... ) |
Square Square (geometry) In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles... (2-orthoplex Cross-polytope In geometry, a cross-polytope, orthoplex, hyperoctahedron, or cocube is a regular, convex polytope that exists in any number of dimensions. The vertices of a cross-polytope are all the permutations of . The cross-polytope is the convex hull of its vertices... ) (2-cube Hypercube In geometry, a hypercube is an n-dimensional analogue of a square and a cube . It is a closed, compact, convex figure whose 1-skeleton consists of groups of opposite parallel line segments aligned in each of the space's dimensions, perpendicular to each other and of the same length.An... ) |
Pentagon Pentagon In geometry, a pentagon is any five-sided polygon. A pentagon may be simple or self-intersecting. The sum of the internal angles in a simple pentagon is 540°. A pentagram is an example of a self-intersecting pentagon.- Regular pentagons :In a regular pentagon, all sides are equal in length and... |
Hexagon | Heptagon | Octagon |
|---|---|---|---|---|---|---|
| Schläfli | {3} | {4} | {5} | {6} | {7} | {8} |
| Dynkin Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... |
||||||
| Image |  |
 |
 |
 |
 |
 |
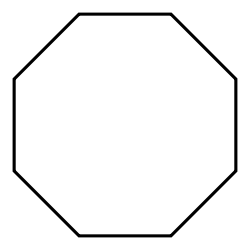There is also an infinite set of star polygons (one for each rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
greater than 2), but these are non-convex. The simplest example is the pentagram
Pentagram
A pentagram is the shape of a five-pointed star drawn with five straight strokes...
, which corresponds to the rational number 5/2.
| Name | Pentagram Pentagram A pentagram is the shape of a five-pointed star drawn with five straight strokes... |
Heptagram Heptagram A heptagram or septegram is a seven-pointed star drawn with seven straight strokes.- Geometry :In general, a heptagram is any self-intersecting heptagon .... s |
Octagram Octagram In geometry, an octagram is an eight-sided star polygon.- Geometry :In general, an octagram is any self-intersecting octagon .... |
Enneagrams Enneagram (geometry) In geometry, an enneagram is a nine-pointed geometric figure. It is sometimes called a nonagram.-Regular enneagram:A regular enneagram is constructed using the same points as the regular enneagon but connected in fixed steps... |
Decagram | ...n-agrams | ||
|---|---|---|---|---|---|---|---|---|
| Schläfli | {5/2} | {7/2} | {7/3} | {8/3} | {9/2} | {9/4} | {10/3} | {p/q} |
| Dynkin Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... |
||||||||
| Image |  |
 |
 |
 |
 |
 |
 |
|
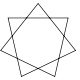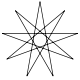Regular polygons, represented by Schläfli symbol {p} for a p-gon. Regular polygons are self-dual, so the rectification produces the same polygon. The uniform truncation operation doubles the sides to {2p}. The snub operation, alternating the truncation, restores the original polygon {p}. Thus all uniform polygons are also regular. The following operations can be performed on regular polygons to derive the uniform polygons:
| Operation | Extended Schläfli Symbols |
Regular result |
Coxeter- Dynkin Diagram Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... |
Position | |
|---|---|---|---|---|---|
| (1) | (0) | ||||
| Parent | t0{p} | {p} | {} | -- | |
| Rectified (Dual) |
t1{p} | {p} | -- | {} | |
| Truncated | t0,1{p} | {2p} | {} | {} | |
| Snub | s{p} | {p} | -- | -- |
Three dimensions
In three dimensions, the situation gets more interesting. There are five regular polyhedra, known as the Platonic solidPlatonic solid
In geometry, a Platonic solid is a convex polyhedron that is regular, in the sense of a regular polygon. Specifically, the faces of a Platonic solid are congruent regular polygons, with the same number of faces meeting at each vertex; thus, all its edges are congruent, as are its vertices and...
s:
| Name | Schläfli {p,q} |
Dynkin Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... |
Image (transparent) |
Image (solid) |
Image (sphere) |
Faces Face (geometry) In geometry, a face of a polyhedron is any of the polygons that make up its boundaries. For example, any of the squares that bound a cube is a face of the cube... {p} |
Edges Edge (geometry) In geometry, an edge is a one-dimensional line segment joining two adjacent zero-dimensional vertices in a polygon. Thus applied, an edge is a connector for a one-dimensional line segment and two zero-dimensional objects.... |
Vertices Vertex (geometry) In geometry, a vertex is a special kind of point that describes the corners or intersections of geometric shapes.-Of an angle:... {q} |
Symmetry Symmetry group The symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation... |
Dual Dual polyhedron In geometry, polyhedra are associated into pairs called duals, where the vertices of one correspond to the faces of the other. The dual of the dual is the original polyhedron. The dual of a polyhedron with equivalent vertices is one with equivalent faces, and of one with equivalent edges is another... |
|---|---|---|---|---|---|---|---|---|---|---|
| Tetrahedron Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids... (3-simplex Simplex In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,... ) (Pyramid) |
{3,3} |  |
 |
4 {3} |
6 | 4 {3} |
Td | (self) | ||
| Cube Cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and... (3-cube Hypercube In geometry, a hypercube is an n-dimensional analogue of a square and a cube . It is a closed, compact, convex figure whose 1-skeleton consists of groups of opposite parallel line segments aligned in each of the space's dimensions, perpendicular to each other and of the same length.An... ) (Hexahedron) |
{4,3} |  |
 |
 |
6 {4} |
12 | 8 {3} |
Oh | Octahedron | |
| Octahedron Octahedron In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex.... (3-orthoplex Cross-polytope In geometry, a cross-polytope, orthoplex, hyperoctahedron, or cocube is a regular, convex polytope that exists in any number of dimensions. The vertices of a cross-polytope are all the permutations of . The cross-polytope is the convex hull of its vertices... ) |
{3,4} |  |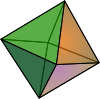
 |
 |
8 {3} |
12 | 6 {4} |
Oh | Cube | |
| Dodecahedron | {5,3} |  |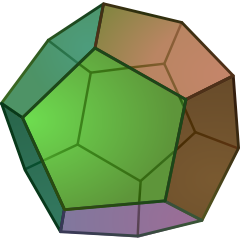
 |
 |
12 {5} |
30 | 20 {3}2 |
Ih | Icosahedron | |
| Icosahedron Icosahedron In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids.... |
{3,5} |  |
 |
 |
20 {3} |
30 | 12 {5} |
Ih | Dodecahedron |
In addition to these, there are also 13 semiregular polyhedra, or Archimedean solid
Archimedean solid
In geometry an Archimedean solid is a highly symmetric, semi-regular convex polyhedron composed of two or more types of regular polygons meeting in identical vertices...
s, which can be obtained via Wythoff construction
Wythoff construction
In geometry, a Wythoff construction, named after mathematician Willem Abraham Wythoff, is a method for constructing a uniform polyhedron or plane tiling. It is often referred to as Wythoff's kaleidoscopic construction.- Construction process :...
s, or by performing operations such as truncation
Truncation (geometry)
In geometry, a truncation is an operation in any dimension that cuts polytope vertices, creating a new facet in place of each vertex.- Uniform truncation :...
on the Platonic solids, as demonstrated in the following table:
| Parent | Truncated | Rectified | Bitruncated (tr. dual) |
Birectified (dual) |
Cantellated | Omnitruncated (Cantitruncated) |
Snub | |
|---|---|---|---|---|---|---|---|---|
| Tetrahedral Tetrahedral symmetry 150px|right|thumb|A regular [[tetrahedron]], an example of a solid with full tetrahedral symmetryA regular tetrahedron has 12 rotational symmetries, and a symmetry order of 24 including transformations that combine a reflection and a rotation.The group of all symmetries is isomorphic to the group... 3-3-2 |
 {3,3} Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids... |
 (3.6.6) Truncated tetrahedron In geometry, the truncated tetrahedron is an Archimedean solid. It has 4 regular hexagonal faces, 4 regular triangular faces, 12 vertices and 18 edges.- Area and volume :... |
 (3.3.3.3) Octahedron In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex.... |
 (3.6.6) Truncated tetrahedron In geometry, the truncated tetrahedron is an Archimedean solid. It has 4 regular hexagonal faces, 4 regular triangular faces, 12 vertices and 18 edges.- Area and volume :... |
 {3,3} Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids... |
 (3.4.3.4) Cuboctahedron In geometry, a cuboctahedron is a polyhedron with eight triangular faces and six square faces. A cuboctahedron has 12 identical vertices, with two triangles and two squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such it is a quasiregular polyhedron,... |
 (4.6.6) Truncated octahedron In geometry, the truncated octahedron is an Archimedean solid. It has 14 faces , 36 edges, and 24 vertices. Since each of its faces has point symmetry the truncated octahedron is a zonohedron.... |
 (3.3.3.3.3) Icosahedron In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids.... |
| Octahedral Octahedral symmetry 150px|thumb|right|The [[cube]] is the most common shape with octahedral symmetryA regular octahedron has 24 rotational symmetries, and a symmetry order of 48 including transformations that combine a reflection and a rotation... 4-3-2 |
 {4,3} Cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and... |
 (3.8.8) Truncated cube In geometry, the truncated cube, or truncated hexahedron, is an Archimedean solid. It has 14 regular faces , 36 edges, and 24 vertices.... |
 (3.4.3.4) Cuboctahedron In geometry, a cuboctahedron is a polyhedron with eight triangular faces and six square faces. A cuboctahedron has 12 identical vertices, with two triangles and two squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such it is a quasiregular polyhedron,... |
 (4.6.6) Truncated octahedron In geometry, the truncated octahedron is an Archimedean solid. It has 14 faces , 36 edges, and 24 vertices. Since each of its faces has point symmetry the truncated octahedron is a zonohedron.... |
 {3,4} Octahedron In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex.... |
 (3.4.4.4) |
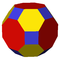 (4.6.8) Truncated cuboctahedron In geometry, the truncated cuboctahedron is an Archimedean solid. It has 12 square faces, 8 regular hexagonal faces, 6 regular octagonal faces, 48 vertices and 72 edges... |
 (3.3.3.3.4) Snub cube In geometry, the snub cube, or snub cuboctahedron, is an Archimedean solid.The snub cube has 38 faces, 6 of which are squares and the other 32 are equilateral triangles. It has 60 edges and 24 vertices. It is a chiral polyhedron, that is, it has two distinct forms, which are mirror images of each... |
| Icosahedral Icosahedral symmetry A regular icosahedron has 60 rotational symmetries, and a symmetry order of 120 including transformations that combine a reflection and a rotation... 5-3-2 |
 {5,3} |
 (3.10.10) Truncated dodecahedron In geometry, the truncated dodecahedron is an Archimedean solid. It has 12 regular decagonal faces, 20 regular triangular faces, 60 vertices and 90 edges.- Geometric relations :... |
 (3.5.3.5) Icosidodecahedron In geometry, an icosidodecahedron is a polyhedron with twenty triangular faces and twelve pentagonal faces. An icosidodecahedron has 30 identical vertices, with two triangles and two pentagons meeting at each, and 60 identical edges, each separating a triangle from a pentagon... |
 (5.6.6) Truncated icosahedron In geometry, the truncated icosahedron is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids whose faces are two or more types of regular polygons.It has 12 regular pentagonal faces, 20 regular hexagonal faces, 60 vertices and 90 edges.... |
 {3,5} Icosahedron In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids.... |
 (3.4.5.4) Rhombicosidodecahedron In geometry, the rhombicosidodecahedron, or small rhombicosidodecahedron, is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids constructed of two or more types of regular polygon faces.... |
 (4.6.10) Truncated icosidodecahedron In geometry, the truncated icosidodecahedron is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids constructed by two or more types of regular polygon faces.... |
 (3.3.3.3.5) Snub dodecahedron In geometry, the snub dodecahedron, or snub icosidodecahedron, is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids constructed by two or more types of regular polygon faces.... |
There is also the infinite set of prisms
Prism (geometry)
In geometry, a prism is a polyhedron with an n-sided polygonal base, a translated copy , and n other faces joining corresponding sides of the two bases. All cross-sections parallel to the base faces are the same. Prisms are named for their base, so a prism with a pentagonal base is called a...
, one for each regular polygon, and a corresponding set of antiprism
Antiprism
In geometry, an n-sided antiprism is a polyhedron composed of two parallel copies of some particular n-sided polygon, connected by an alternating band of triangles...
s.
| # | Name | Picture | Tiling | Vertex figure Vertex figure In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:... |
Coxeter-Dynkin Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... and Schläfli symbols |
|---|---|---|---|---|---|
| P2p | Prism Prism (geometry) In geometry, a prism is a polyhedron with an n-sided polygonal base, a translated copy , and n other faces joining corresponding sides of the two bases. All cross-sections parallel to the base faces are the same. Prisms are named for their base, so a prism with a pentagonal base is called a... |
 |
 |
 |
t{2,p} |
| Ap | Antiprism Antiprism In geometry, an n-sided antiprism is a polyhedron composed of two parallel copies of some particular n-sided polygon, connected by an alternating band of triangles... |
 |
 |
 |
t{2,p} |
The nonconvex uniform polyhedra include a further 4 regular polyhedra, the Kepler-Poinsot polyhedra, and 53 semiregular nonconvex polyhedra. There are also two infinite sets, the star prisms (one for each star polygon) and star antiprisms (one for each rational number greater than 3/2).
Constructions
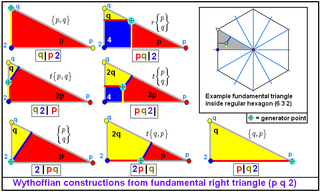
The Wythoffian uniform polyhedra and tilings can be defined by their Wythoff symbolWythoff symbol
In geometry, the Wythoff symbol was first used by Coxeter, Longeut-Higgens and Miller in their enumeration of the uniform polyhedra. It represents a construction by way of Wythoff's construction applied to Schwarz triangles....
, which specifies the fundamental region of the object. An extension of Schläfli notation, also used by Coxeter
Harold Scott MacDonald Coxeter
Harold Scott MacDonald "Donald" Coxeter, was a British-born Canadian geometer. Coxeter is regarded as one of the great geometers of the 20th century. He was born in London but spent most of his life in Canada....
, applies to all dimensions; it consists of the letter 't', followed by a series of subscripted numbers corresponding to the ringed nodes of the Coxeter-Dynkin diagram
Coxeter-Dynkin diagram
In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors...
, and followed by the Schläfli symbol of the regular seed polytope. For example, the truncated octahedron
Truncated octahedron
In geometry, the truncated octahedron is an Archimedean solid. It has 14 faces , 36 edges, and 24 vertices. Since each of its faces has point symmetry the truncated octahedron is a zonohedron....
is represented by the notation: t0,1{3,4}.
| Operation | Extended Schläfli Symbols |
Coxeter- Dynkin Diagram Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... |
Wythoff symbol Wythoff construction In geometry, a Wythoff construction, named after mathematician Willem Abraham Wythoff, is a method for constructing a uniform polyhedron or plane tiling. It is often referred to as Wythoff's kaleidoscopic construction.- Construction process :... |
Position | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| (2) | (1) | (0) | (0,1) | (0,2) | (1,2) | |||||
| Parent |  |
t0{p,q} | q | 2 p | {p} | {} | -- | -- | -- | {} | |
| Rectified Rectification (geometry) In Euclidean geometry, rectification is the process of truncating a polytope by marking the midpoints of all its edges, and cutting off its vertices at those points... |
 |
t1{p,q} | 2 | p q | {p} | -- | {q} | -- | {} | -- | |
| Birectified (or dual Dual polyhedron In geometry, polyhedra are associated into pairs called duals, where the vertices of one correspond to the faces of the other. The dual of the dual is the original polyhedron. The dual of a polyhedron with equivalent vertices is one with equivalent faces, and of one with equivalent edges is another... ) |
 |
t2{p,q} | p | 2 q | -- | {} | {q} | {} | -- | -- | |
| Truncated Truncation (geometry) In geometry, a truncation is an operation in any dimension that cuts polytope vertices, creating a new facet in place of each vertex.- Uniform truncation :... |
 |
t0,1{p,q} | 2 q | p | {2p} | {} | {q} | -- | {} | {} | |
| Bitruncated (or truncated dual) |
 |
t1,2{p,q} | 2 p | q | {p} | {} | {2q} | {} | {} | -- | |
| Cantellated Cantellation (geometry) In geometry, a cantellation is an operation in any dimension that cuts a regular polytope at its edges and vertices, creating a new facet in place of each edge and vertex. The operation also applies to regular tilings and honeycombs... (or expanded Expansion (geometry) In geometry, expansion is a polytope operation where facets are separated and moved radially apart, and new facets are formed at separated elements... ) |
 |
t0,2{p,q} | p q | 2 | {p} | {}x{} | {q} | {} | -- | {} | |
| Cantitruncated (or omnitruncated) |
 |
t0,1,2{p,q} | 2 p q | | {2p} | {}x{} | {2q} | {} | {} | {} | |
| Snub Snub (geometry) In geometry, an alternation is an operation on a polyhedron or tiling that removes alternate vertices. Only even-sided polyhedra can be alternated, for example the zonohedra. Every 2n-sided face becomes n-sided... |
 |
s{p,q} | | 2 p q | {p} | {3} {3} |
{q} | -- | -- | -- |
 |
 Generating triangles |
Four dimensions
In four dimensions, there are 6 convex regular polychora, 17 prisms on the Platonic and Archimedean solids (excluding the cube-prism, which has already been counted as the tesseractTesseract
In geometry, the tesseract, also called an 8-cell or regular octachoron or cubic prism, is the four-dimensional analog of the cube. The tesseract is to the cube as the cube is to the square. Just as the surface of the cube consists of 6 square faces, the hypersurface of the tesseract consists of 8...
), and two infinite sets: the prisms on the convex antiprisms, and the duoprism
Duoprism
In geometry of 4 dimensions or higher, a duoprism is a polytope resulting from the Cartesian product of two polytopes, each of two dimensions or higher...
s. There are also 41 convex semiregular polychora, including the non-Wythoffian grand antiprism
Grand antiprism
In geometry, the grand antiprism or pentagonal double antiprismoid is a uniform polychoron bounded by 320 cells: 20 pentagonal antiprisms, and 300 tetrahedra. It is an anomalous, non-Wythoffian uniform polychoron, discovered in 1965 by Conway and Guy.- Alternate names :* Pentagonal double...
and the snub 24-cell
Snub 24-cell
In geometry, the snub 24-cell is a convex uniform polychoron composed of 120 regular tetrahedral and 24 icosahedral cells. Five tetrahedra and three icosahedra meet at each vertex. In total it has 480 triangular faces, 432 edges, and 96 vertices....
. Both of these special polychora are composed of subgroups of the vertices of the 600-cell.
The four-dimensional nonconvex uniform polytopes have not all been enumerated. The ones that have include the 10 regular nonconvex polychora (Schläfli-Hess polychora) and 57 prisms on the nonconvex uniform polyhedra, as well as three infinite families: the prisms on the star antiprisms, the duoprisms formed by multiplying
Cartesian product
In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
two star polygons, and the duoprisms formed by multiplying an ordinary polygon with a star polygon. There is an unknown number of polychora that do not fit into the above categories; over one thousand have been discovered so far.
Hyperplane
A hyperplane is a concept in geometry. It is a generalization of the plane into a different number of dimensions.A hyperplane of an n-dimensional space is a flat subset with dimension n − 1...
, but it is more convenient for our purposes to consider only its two-dimensional intersection with the three-dimensional surface of the hypersphere
Hypersphere
In mathematics, an n-sphere is a generalization of the surface of an ordinary sphere to arbitrary dimension. For any natural number n, an n-sphere of radius r is defined as the set of points in -dimensional Euclidean space which are at distance r from a central point, where the radius r may be any...
; thus the mirrors form an irregular tetrahedron
Tetrahedron
In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...
.
Each of the sixteen regular polychora is generated by one of four symmetry groups, as follows:
- group [3,3,3]: the 5-cell {3,3,3}, which is self-dual;
- group [3,3,4]: 16-cell16-cellIn four dimensional geometry, a 16-cell or hexadecachoron is a regular convex 4-polytope. It is one of the six regular convex 4-polytopes first described by the Swiss mathematician Ludwig Schläfli in the mid-19th century....
{3,3,4} and its dual tesseractTesseractIn geometry, the tesseract, also called an 8-cell or regular octachoron or cubic prism, is the four-dimensional analog of the cube. The tesseract is to the cube as the cube is to the square. Just as the surface of the cube consists of 6 square faces, the hypersurface of the tesseract consists of 8...
{4,3,3}; - group [3,4,3]: the 24-cell {3,4,3}, self-dual;
- group [3,3,5]: 600-cell {3,3,5}, its dual 120-cell {5,3,3}, and their ten regular stellations.
- group [31,1,1]: contains only repeated members of the [3,3,4] family.
(The groups are named in Coxeter
Harold Scott MacDonald Coxeter
Harold Scott MacDonald "Donald" Coxeter, was a British-born Canadian geometer. Coxeter is regarded as one of the great geometers of the 20th century. He was born in London but spent most of his life in Canada....
notation.)
Eight of the convex uniform honeycomb
Convex uniform honeycomb
In geometry, a convex uniform honeycomb is a uniform tessellation which fills three-dimensional Euclidean space with non-overlapping convex uniform polyhedral cells.Twenty-eight such honeycombs exist:* the familiar cubic honeycomb and 7 truncations thereof;...
s in Euclidean 3-space are analogously generated from the cubic honeycomb
Cubic honeycomb
The cubic honeycomb is the only regular space-filling tessellation in Euclidean 3-space, made up of cubic cells. It has 4 cubes around every edge, and 8 cubes around each vertex. Its vertex figure is a regular octahedron....
{4,3,4}, by applying the same operations used to generate the Wythoffian uniform polychora.
For a given symmetry simplex, a generating point may be placed on any of the four vertices, 6 edges, 4 faces, or the interior volume. On each of these 15 elements there is a point whose images, reflected in the four mirrors, are the vertices of a uniform polychoron.
The extended Schläfli symbols are made by a t followed by inclusion of one to four subscripts 0,1,2,3. If there's one subscript, the generating point is on a corner of the fundamental region, i.e. a point where three mirrors meet. These corners are notated as
- 0: vertex of the parent polychoron (center of the dual's cell)
- 1: center of the parent's edge (center of the dual's face)
- 2: center of the parent's face (center of the dual's edge)
- 3: center of the parent's cell (vertex of the dual)
(For the two self-dual polychora, "dual" means a similar polychoron in dual position.) Two or more subscripts mean that the generating point is between the corners indicated.
Constructive summary
The 15 constructive forms by family are summarized below. The self-dual families are listed in one column, and others as two columns with shared entries on the symmetric Coxeter-Dynkin diagramCoxeter-Dynkin diagram
In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors...
s. The final 10th row lists the snub 24-cell constructions. This includes all nonprismatic uniform polychora, except for the non-Wythoffian grand antiprism
Grand antiprism
In geometry, the grand antiprism or pentagonal double antiprismoid is a uniform polychoron bounded by 320 cells: 20 pentagonal antiprisms, and 300 tetrahedra. It is an anomalous, non-Wythoffian uniform polychoron, discovered in 1965 by Conway and Guy.- Alternate names :* Pentagonal double...
, which has no Coxeter family.
| A4 | BC4 | D4 | F4 | GH4 | ||
|---|---|---|---|---|---|---|
| [4,3,3] |
1,1,1] |
[5,3,3] |
||||
5-cell {3,3,3} |
16-cell 16-cell In four dimensional geometry, a 16-cell or hexadecachoron is a regular convex 4-polytope. It is one of the six regular convex 4-polytopes first described by the Swiss mathematician Ludwig Schläfli in the mid-19th century....  {3,3,4} |
tesseract Tesseract In geometry, the tesseract, also called an 8-cell or regular octachoron or cubic prism, is the four-dimensional analog of the cube. The tesseract is to the cube as the cube is to the square. Just as the surface of the cube consists of 6 square faces, the hypersurface of the tesseract consists of 8... 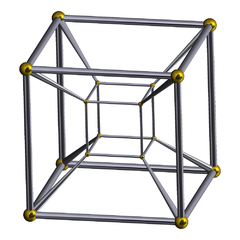 {4,3,3} |
demitesseract {31,1,1} |
24-cell {3,4,3} |
600-cell {3,3,5} |
120-cell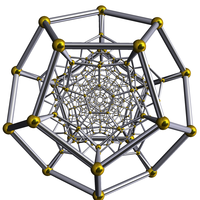 {5,3,3} |
| rectified 5-cell Rectified 5-cell In four dimensional geometry, the rectified 5-cell is a uniform polychoron composed of 5 regular tetrahedral and 5 regular octahedral cells. Each edge has one tetrahedron and two octahedra. Each vertex has two tetrahedra and three octahedra. In total it has 30 triangle faces, 30 edges, and 10...  t1{3,3,3} |
rectified 16-cell t1{3,3,4} |
rectified tesseract Rectified tesseract In geometry, the rectified tesseract, or rectified 8-cell is a uniform polychoron bounded by 24 cells: 8 cuboctahedra, and 16 tetrahedra....  t1{4,3,3} |
rectified demitesseract t1{31,1,1} |
rectified 24-cell Rectified 24-cell In geometry, the rectified 24-cell is a uniform 4-dimensional polytope , which is bounded by 48 cells: 24 cubes, and 24 cuboctahedra. It can be obtained by reducing the icositetrachoron's cells to cubes or cuboctahedra.... 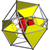 t1{3,4,3} |
rectified 600-cell Rectified 600-cell In geometry, a rectified 600-cell is a uniform polychoron formed as the rectification of the regular 600-cell.There are four rectifications of the 600-cell, including the zeroth, the 600-cell itself... t1{3,3,5} |
rectified 120-cell Rectified 120-cell In geometry, a rectified 120-cell is a uniform polychoron formed as the rectification of the regular 120-cell.There are four rectifications of the 120-cell, including the zeroth, the 120-cell itself... t1{5,3,3} |
| truncated 5-cell Truncated 5-cell In geometry, a truncated 5-cell is a uniform polychoron formed as the truncation of the regular 5-cell.There are two degrees of trunctions, including a bitruncation.- Truncated 5-cell:... 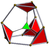 t0,1{3,3,3} |
truncated 16-cell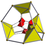 t0,1{3,3,4} |
truncated tesseract Truncated tesseract In geometry, a truncated tesseract is a uniform polychoron formed as the truncation of the regular tesseract.There are three trunctions, including a bitruncation, and a tritruncation, which creates the truncated 16-cell....  t0,1{4,3,3} |
truncated demitesseract t0,1{31,1,1} |
truncated 24-cell Truncated 24-cell In geometry, a truncated 5-cell is a uniform polychoron formed as the truncation of the regular 5-cell.There are two degrees of trunctions, including a bitruncation.- Truncated 5-cell:...  t0,1{3,4,3} |
 t0,1{3,3,5} |
truncated 120-cell Truncated 120-cell In geometry, a truncated 120-cell is a uniform polychoron formed as the truncation of the regular 120-cell.There are three trunctions, including a bitruncation, and a tritruncation, which creates the truncated 600-cell.... 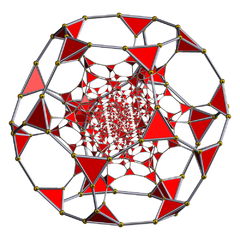 t0,1{5,3,3} |
| cantellated 5-cell Cantellated 5-cell In four-dimensional geometry, a cantellated 5-cell is a convex uniform polychoron, being a cantellation of the regular 5-cell.There are 2 unique degrees of runcinations of the 5-cell including with permutations truncations....  t0,2{3,3,3} |
cantellated 16-cell Rectified 24-cell In geometry, the rectified 24-cell is a uniform 4-dimensional polytope , which is bounded by 48 cells: 24 cubes, and 24 cuboctahedra. It can be obtained by reducing the icositetrachoron's cells to cubes or cuboctahedra.... t0,2{3,3,4} |
cantellated tesseract Cantellated tesseract In four-dimensional geometry, a cantellated tesseract is a convex uniform polychoron, being a cantellation of the regular tesseract.There are four degrees of cantellations of the tesseract including with permutations truncations...  t0,2{4,3,3} |
cantellated demitesseract t0,2{31,1,1} |
cantellated 24-cell Cantellated 24-cell In four-dimensional geometry, a cantellated 24-cell is a convex uniform polychoron, being a cantellation of the regular 24-cell.There are 2 unique degrees of runcinations of the 24-cell including with permutations truncations....  t0,2{3,4,3} |
 t0,2{3,3,5} |
cantellated 120-cell Cantellated 120-cell In four-dimensional geometry, a cantellated 120-cell is a convex uniform polychoron, being a cantellation of the regular 120-cell....  t0,2{5,3,3} |
runcinated 5-cell t0,3{3,3,3} |
runcinated 16-cell Runcinated tesseract In four-dimensional geometry, a runcinated tesseract is a convex uniform polychoron, being a runcination of the regular tesseract....  t0,3{3,3,4} |
runcinated tesseract Runcinated tesseract In four-dimensional geometry, a runcinated tesseract is a convex uniform polychoron, being a runcination of the regular tesseract.... 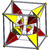 t0,3{4,3,3} |
runcinated 24-cell Runcinated 24-cell In four-dimensional geometry, a runcinated 24-cell is a convex uniform polychoron, being a runcination of the regular 24-cell.... t0,3{3,4,3} |
runcinated 600-cell runcinated 120-cell Runcinated 120-cell In four-dimensional geometry, a runcinated 120-cell is a convex uniform polychoron, being a runcination of the regular 120-cell....  t0,3{3,3,5} |
||
bitruncated 5-cell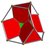 t1,2{3,3,3} |
bitruncated 16-cell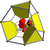 t1,2{3,3,4} |
bitruncated tesseract t1,2{4,3,3} |
bitruncated 24-cell t1,2{3,4,3} |
bitruncated 600-cell bitruncated 120-cell t1,2{3,3,5} |
||
cantitruncated 5-cell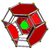 t0,1,2{3,3,3} |
cantitruncated 16-cell Truncated 24-cell In geometry, a truncated 5-cell is a uniform polychoron formed as the truncation of the regular 5-cell.There are two degrees of trunctions, including a bitruncation.- Truncated 5-cell:... 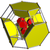 t0,1,2{3,3,4} |
cantitruncated tesseract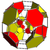 t0,1,2{4,3,3} |
cantitruncated demitesseract t0,1,2{31,1,1} |
cantitruncated 24-cell t0,1,2{3,4,3} |
 t0,1,2{3,3,5} |
 t0,1,2{5,3,3} |
runcitruncated 5-cell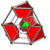 t0,1,3{3,3,3} |
runcitruncated 16-cell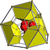 t0,1,3{3,3,4} |
runcitruncated tesseract t0,1,3{4,3,3} |
runcicantellated demitesseract t0,2,3{31,1,1} |
runcitruncated 24-cell t0,1,3{3,4,3} |
 t0,1,3{3,3,5} |
 t0,1,3{5,3,3} |
omnitruncated 5-cell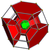 t0,1,2,3{3,3,3} |
omnitruncated 16-cell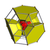 t0,1,2,3{3,3,4} |
omnitruncated tesseract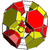 t0,1,2,3{3,3,4} |
omnitruncated demitesseract t0,1,2,3{31,1,1} |
omnitruncated 24-cell t0,1,2,3{3,4,3} |
omnitruncated 120-cell omnitruncated 600-cell  t0,1,2,3{5,3,3} |
|
| alternated cantitruncated 16-cell Snub 24-cell In geometry, the snub 24-cell is a convex uniform polychoron composed of 120 regular tetrahedral and 24 icosahedral cells. Five tetrahedra and three icosahedra meet at each vertex. In total it has 480 triangular faces, 432 edges, and 96 vertices....  h0,1,2{3,3,4} |
snub demitesseract s{31,1,1} |
Alternated truncated 24-cell Snub 24-cell In geometry, the snub 24-cell is a convex uniform polychoron composed of 120 regular tetrahedral and 24 icosahedral cells. Five tetrahedra and three icosahedra meet at each vertex. In total it has 480 triangular faces, 432 edges, and 96 vertices.... h0,1{3,4,3} |
||||
Truncated forms
The following table defines all 15 forms. Each trunction form can have from one to four cell types, located in positions 0,1,2,3 as defined above. The cells are labeled by polyhedral truncation notation.- An n-gonal prism is represented as : {n}x{2}.
- The green background is shown on forms that are equivalent to either the parent or the dual.
- The red background shows the truncations of the parent, and blue the truncations of the dual.
| Operation | Extended Schläfli symbols |
Coxeter- Dynkin Diagram Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... |
Position | |||
|---|---|---|---|---|---|---|
| (3) | (2) | (1) | (0) | |||
| Parent | t0{p,q,r} | {p,q} |
{p} |
{} |
-- |
|
| Rectified Rectification (geometry) In Euclidean geometry, rectification is the process of truncating a polytope by marking the midpoints of all its edges, and cutting off its vertices at those points... |
t1{p,q,r} | t1{p,q} |
{p} |
-- |
{q,r} |
|
| Birectified (or rectified dual) |
t2{p,q,r} | {q,p} |
-- |
{r} |
t1{q,r} |
|
| Trirectifed (or dual) |
t3{p,q,r} | -- |
{} |
{r} |
t2{q,r} |
|
| Truncated Truncation (geometry) In geometry, a truncation is an operation in any dimension that cuts polytope vertices, creating a new facet in place of each vertex.- Uniform truncation :... |
t0,1{p,q,r} | t0,1{p,q} |
{2p} |
{} |
{q,r} |
|
| Bitruncated | t1,2{p,q,r} | t1,2{p,q} |
{p} |
{r} |
t0,1{q,r} |
|
| Tritruncated (or truncated dual) |
t2,3{p,q,r} | {q,p} |
{} |
{2r} |
t1,2{q,r} |
|
| Cantellated Cantellation (geometry) In geometry, a cantellation is an operation in any dimension that cuts a regular polytope at its edges and vertices, creating a new facet in place of each edge and vertex. The operation also applies to regular tilings and honeycombs... |
t0,2{p,q,r} | t0,2{p,q} |
{p} |
{}x{r} |
t1{q,r} |
|
| Bicantellated (or cantellated dual) |
t1,3{p,q,r} | t1{p,q} |
{p}x{} |
{r} |
t0,2{q,r} |
|
| Runcinated (or expanded Expansion (geometry) In geometry, expansion is a polytope operation where facets are separated and moved radially apart, and new facets are formed at separated elements... ) |
t0,3{p,q,r} | {p,q} |
{p}x{} |
{}x{r} |
t2{q,r} |
|
| Cantitruncated | t0,1,2{p,q,r} | t0,1,2{p,q} |
{2p} |
{}x{r} |
t0,1{q,r} |
|
| Bicantitruncated (or cantitruncated dual) |
t1,2,3{p,q,r} | t1,2{p,q} |
{p}x{} |
{2r} |
t0,1,2{q,r} |
|
| Runcitruncated | t0,1,3{p,q,r} | t0,1{p,q} |
{2p}x{} |
{}x{r} |
t0,2{q,r} |
|
| Runcicantellated (or runcitruncated dual) |
t0,2,3{p,q,r} | t0,1,2{p,q} |
{p}x{} |
{}x{2r} |
t1,2{q,r} |
|
| Runcicantitruncated (or omnitruncated) |
t0,1,2,3{p,q,r} | t0,1,2{p,q} |
{2p}x{} |
{}x{2r} |
t0,1,2{q,r} |
Five and higher dimensions
In five and higher dimensions, there are 3 regular polytopes, the hypercubeHypercube
In geometry, a hypercube is an n-dimensional analogue of a square and a cube . It is a closed, compact, convex figure whose 1-skeleton consists of groups of opposite parallel line segments aligned in each of the space's dimensions, perpendicular to each other and of the same length.An...
, simplex
Simplex
In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...
and cross-polytope
Cross-polytope
In geometry, a cross-polytope, orthoplex, hyperoctahedron, or cocube is a regular, convex polytope that exists in any number of dimensions. The vertices of a cross-polytope are all the permutations of . The cross-polytope is the convex hull of its vertices...
. They are generalisations of the three-dimensional cube, tetrahedron and octahedron, respectively. There are no regular star polytopes in these dimensions. Most uniform higher-dimensional polytopes are obtained by modifying the regular polytopes, or by taking the Cartesian product of polytopes of lower dimensions.
In six, seven and eight dimensions, the exceptional
Exceptional object
Many branches of mathematics study objects of a given type and prove a classification theorem. A common theme is that the classification results in a number of series of objects as well as a finite number of exceptions that don't fit into any series. These are known as exceptional...
simple Lie group
Simple Lie group
In group theory, a simple Lie group is a connected non-abelian Lie group G which does not have nontrivial connected normal subgroups.A simple Lie algebra is a non-abelian Lie algebra whose only ideals are 0 and itself...
s, E6, E7 and E8
E8 (mathematics)
In mathematics, E8 is any of several closely related exceptional simple Lie groups, linear algebraic groups or Lie algebras of dimension 248; the same notation is used for the corresponding root lattice, which has rank 8...
come into play. By placing rings on a nonzero number of nodes of the Coxeter-Dynkin diagram
Coxeter-Dynkin diagram
In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors...
s, one can obtain 63 new 6-polytopes, 127 new 7-polytopes and 255 new 8-polytopes. A notable example is the Gosset 421 polytope
Gosset 4 21 polytope
In 8-dimensional geometry, the 421 is a semiregular uniform 8-polytope, constructed within the symmetry of the E8 group. It was discovered by Thorold Gosset, published in his 1900 paper...
.
Uniform honeycombs
Related to the subject of finite uniform polytopes are uniform honeycombs in Euclidean and hyperbolic spaces. Euclidean uniform honeycombs are generated by Affine Coxeter groups and hyperbolic honeycombs are generated by the Coxeter-Dynkin diagram#Hyperbolic Coxeter groups. Two affine Coxeter groups can be multiplied togetherThere are two classes of hyperbolic Coxeter groups, compact and noncompact. Uniform honeycombs generated by compact groups have finite facets and vertex figures, and exist from 2 to 4 dimensions. Noncompact groups have affine or hyperbolic subgraphs, and infinite facets or vertex figures, and exist from 3 to 10 dimensions.
External links
- uniform, convex polytopes in four dimensions:, Marco Möller