
Cantellated 120-cell
Encyclopedia
120-cell |
Cantellated 120-cell |
Cantellated 600-cell |
600-cell |
Cantitruncated 120-cell |
Cantitruncated 600-cell |
| Orthogonal projections in H3 Coxeter plane | ||
|---|---|---|
In four-dimensional geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, a cantellated 120-cell is a convex uniform polychoron
Uniform polychoron
In geometry, a uniform polychoron is a polychoron or 4-polytope which is vertex-transitive and whose cells are uniform polyhedra....
, being a cantellation (a 2nd order truncation) of the regular 120-cell.
There are four degrees of cantellations of the 120-cell including with permutations truncations. Two are expressed relative to the dual 600-cell.
Cantellated 120-cell
| Cantellated 120-cell | |
|---|---|
| Type | Uniform polychoron Uniform polychoron In geometry, a uniform polychoron is a polychoron or 4-polytope which is vertex-transitive and whose cells are uniform polyhedra.... |
| Uniform index | 37 |
| Coxeter-Dynkin diagram Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... |
|
| Cells | 1920 total: 120 (3.4.5.4)  1200 (3.4.4) Triangular prism In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides....  600 (3.3.3.3) Octahedron In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....  |
| Faces | 4800{3}+3600{4}+720{5} |
| Edges | 10800 |
| Vertices | 3600 |
| Vertex figure Vertex figure In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:... |
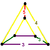 wedge Wedge (geometry) In solid geometry, a wedge is a polyhedron defined by two triangles and three trapezoid faces. A wedge has five faces, nine edges, and six vertices.A wedge is a subclass of the prismatoids with the base and opposite ridge in two parallel planes.... |
| Schläfli symbol | t0,2{5,3,3} |
| Symmetry group Coxeter group In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example... |
H4, [3,3,5] |
| Properties | convex Convex polytope A convex polytope is a special case of a polytope, having the additional property that it is also a convex set of points in the n-dimensional space Rn... |
The cantellated 120-cell is a uniform polychoron
Uniform polychoron
In geometry, a uniform polychoron is a polychoron or 4-polytope which is vertex-transitive and whose cells are uniform polyhedra....
. It is named by its construction as a Cantellation
Cantellation (geometry)
In geometry, a cantellation is an operation in any dimension that cuts a regular polytope at its edges and vertices, creating a new facet in place of each edge and vertex. The operation also applies to regular tilings and honeycombs...
operation applied to the regular 120-cell. It contains 1920 cells
Cell (geometry)
In geometry, a cell is a three-dimensional element that is part of a higher-dimensional object.- In polytopes :A cell is a three-dimensional polyhedron element that is part of the boundary of a higher-dimensional polytope, such as a polychoron or honeycomb For example, a cubic honeycomb is made...
, including 120 rhombicosidodecahedra
Rhombicosidodecahedron
In geometry, the rhombicosidodecahedron, or small rhombicosidodecahedron, is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids constructed of two or more types of regular polygon faces....
, 1200 triangular prism
Triangular prism
In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides....
s, 600 octahedra
Octahedron
In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....
. Its vertex figure is a wedge
Wedge (geometry)
In solid geometry, a wedge is a polyhedron defined by two triangles and three trapezoid faces. A wedge has five faces, nine edges, and six vertices.A wedge is a subclass of the prismatoids with the base and opposite ridge in two parallel planes....
, with two rhombicosidodecahedra, two triangular prisms, and one octahedron meeting at each vertex.
Alternative names
- Cantellated 120-cell Norman Johnson
- Cantellated hecatonicosachoron / Cantellated polydodecahedron
- Small rhombated hecatonicosachoron (Acronym srahi)(George OlshevskyGeorge OlshevskyGeorge Olshevsky is a freelance editor, writer, publisher, amateur paleontologist, and mathematician living in San Diego, California.Olshevsky maintains the comprehensive online Dinosaur Genera List...
and Jonathan Bowers) - Ambo-02 polydodecahedron (John ConwayJohn ConwayJohn Conway may refer to:* John Horton Conway, mathematician at Princeton University. Popularly known for Conway's Game of Life* John B. Conway, mathematician, functional analyst, George Washington University...
)
Images
| H3 | A2 / B3 / D4 |
|---|---|
[10] |
[6] |
 Schlegel diagram. Pentagonal face are removed. |
Cantitruncated 120-cell
| Cantitruncated 120-cell | |
|---|---|
| Type | Uniform polychoron Uniform polychoron In geometry, a uniform polychoron is a polychoron or 4-polytope which is vertex-transitive and whose cells are uniform polyhedra.... |
| Uniform index | 42 |
| Schläfli symbol | t0,1,2{5,3,3} |
| Coxeter-Dynkin diagram Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... |
|
| Cells | 1920 total: 120 (4.6.10) 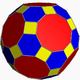 1200 (3.4.4) Triangular prism In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides....  600 (3.6.6) Truncated tetrahedron In geometry, the truncated tetrahedron is an Archimedean solid. It has 4 regular hexagonal faces, 4 regular triangular faces, 12 vertices and 18 edges.- Area and volume :...  |
| Faces | 9120: 2400{3}+3600{4}+ 2400{6}+720{10} |
| Edges | 14400 |
| Vertices | 7200 |
| Vertex figure Vertex figure In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:... |
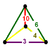 sphenoid Sphenoid Sphenoid may refer to:* In anatomy, the sphenoid bone* In geometry, a tetrahedron with mirror symmetry... |
| Symmetry group Coxeter group In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example... |
H4, [3,3,5] |
| Properties | convex Convex polytope A convex polytope is a special case of a polytope, having the additional property that it is also a convex set of points in the n-dimensional space Rn... |
The cantitruncated 120-cell is a uniform polychoron
Uniform polychoron
In geometry, a uniform polychoron is a polychoron or 4-polytope which is vertex-transitive and whose cells are uniform polyhedra....
.
This polychoron
Polychoron
In geometry, a polychoron or 4-polytope is a four-dimensional polytope. It is a connected and closed figure, composed of lower dimensional polytopal elements: vertices, edges, faces , and cells...
is related to the regular 120-cell. The cantitruncation operation create new truncated tetrahedral cells at the vertices, and triangular prisms at the edges. The original dodecahedron cells are cantitruncated into great rhombicosidodecahedron cells.
The image shows the polychoron drawn as a Schlegel diagram which projects the 4 dimensional figure into 3-space, distorting the sizes of the cells. In addition, the decagon
Decagon
In geometry, a decagon is any polygon with ten sides and ten angles, and usually refers to a regular decagon, having all sides of equal length and each internal angle equal to 144°...
al faces are hidden, allowing us to see the elemented projected inside.
Alternative names
- Cantitruncated 120-cell Norman Johnson
- Cantitruncated hecatonicosachoron / Cantitruncated polydodecahedron
- Great rhombated hecatonicosachoron (Acronym grahi) (George OlshevskyGeorge OlshevskyGeorge Olshevsky is a freelance editor, writer, publisher, amateur paleontologist, and mathematician living in San Diego, California.Olshevsky maintains the comprehensive online Dinosaur Genera List...
and Jonthan Bowers) - Ambo-012 polydodecahedron (John ConwayJohn ConwayJohn Conway may refer to:* John Horton Conway, mathematician at Princeton University. Popularly known for Conway's Game of Life* John B. Conway, mathematician, functional analyst, George Washington University...
)
Images
| H3 | A2 / B3 / D4 |
|---|---|
[10] |
[6] |
 Centered on truncated icosidodecahedron Truncated icosidodecahedron In geometry, the truncated icosidodecahedron is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids constructed by two or more types of regular polygon faces.... cell with decagon Decagon In geometry, a decagon is any polygon with ten sides and ten angles, and usually refers to a regular decagon, having all sides of equal length and each internal angle equal to 144°... al faces hidden. |
Cantellated 600-cell
| Cantellated 600-cell | |
|---|---|
| Type | Uniform polychoron Uniform polychoron In geometry, a uniform polychoron is a polychoron or 4-polytope which is vertex-transitive and whose cells are uniform polyhedra.... |
| Uniform index | 40 |
| Schläfli symbol | t0,2{3,3,5} |
| Coxeter-Dynkin diagram Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... |
|
| Cells | 1440 total: 120  3.5.3.5 3.5.3.5Icosidodecahedron In geometry, an icosidodecahedron is a polyhedron with twenty triangular faces and twelve pentagonal faces. An icosidodecahedron has 30 identical vertices, with two triangles and two pentagons meeting at each, and 60 identical edges, each separating a triangle from a pentagon... 600  3.4.3.4 3.4.3.4Cuboctahedron In geometry, a cuboctahedron is a polyhedron with eight triangular faces and six square faces. A cuboctahedron has 12 identical vertices, with two triangles and two squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such it is a quasiregular polyhedron,... 720  4.4.5 4.4.5Pentagonal prism In geometry, the pentagonal prism is a prism with a pentagonal base. It is a type of heptahedron with 7 faces, 15 edges, and 10 vertices.- As a semiregular polyhedron :... |
| Faces | 8640 total: (1200+2400){3} +3600{4}+1440{5} |
| Edges | 10800 |
| Vertices | 3600 |
| Vertex figure Vertex figure In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:... |
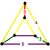 isosceles triangular prism Triangular prism In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides.... |
| Symmetry group Coxeter group In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example... |
H4, [3,3,5] |
| Properties | convex Convex polytope A convex polytope is a special case of a polytope, having the additional property that it is also a convex set of points in the n-dimensional space Rn... |
The cantellated 600-cell is a uniform polychoron
Uniform polychoron
In geometry, a uniform polychoron is a polychoron or 4-polytope which is vertex-transitive and whose cells are uniform polyhedra....
. It has 1440 cells: 120 icosidodecahedra
Icosidodecahedron
In geometry, an icosidodecahedron is a polyhedron with twenty triangular faces and twelve pentagonal faces. An icosidodecahedron has 30 identical vertices, with two triangles and two pentagons meeting at each, and 60 identical edges, each separating a triangle from a pentagon...
, 600 cuboctahedra
Cuboctahedron
In geometry, a cuboctahedron is a polyhedron with eight triangular faces and six square faces. A cuboctahedron has 12 identical vertices, with two triangles and two squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such it is a quasiregular polyhedron,...
, and 720 pentagonal prism
Pentagonal prism
In geometry, the pentagonal prism is a prism with a pentagonal base. It is a type of heptahedron with 7 faces, 15 edges, and 10 vertices.- As a semiregular polyhedron :...
s. Its vertex figure is an isosceles triangular prism
Triangular prism
In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides....
, defined by one icosidodecahedron, two cuboctahedra, and two pentagonal prisms.
Alternative names
- Cantellated 600-cell Norman Johnson
- Cantellated hexacosichoron / Cantellated tetraplex
- Small rhombihexacosichoron (Acronym srix) (George OlshevskyGeorge OlshevskyGeorge Olshevsky is a freelance editor, writer, publisher, amateur paleontologist, and mathematician living in San Diego, California.Olshevsky maintains the comprehensive online Dinosaur Genera List...
and Jonathan Bowers) - Ambo-02 tetraplex (John ConwayJohn ConwayJohn Conway may refer to:* John Horton Conway, mathematician at Princeton University. Popularly known for Conway's Game of Life* John B. Conway, mathematician, functional analyst, George Washington University...
)
Construction
This polychoron has cells at 3 of 4 positions in the fundamental domain, extracted from the Coxeter-Dynkin diagram by removing one node at a time:| Node | Order | Coxeter-Dynkin Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... |
Cell | Picture |
|---|---|---|---|---|
| 0 | 600 | Cantellated tetrahedron (Cuboctahedron Cuboctahedron In geometry, a cuboctahedron is a polyhedron with eight triangular faces and six square faces. A cuboctahedron has 12 identical vertices, with two triangles and two squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such it is a quasiregular polyhedron,... ) |
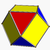 |
|
| 1 | 1200 | None (Degenerate triangular prism) |
||
| 2 | 720 | Pentagonal prism Pentagonal prism In geometry, the pentagonal prism is a prism with a pentagonal base. It is a type of heptahedron with 7 faces, 15 edges, and 10 vertices.- As a semiregular polyhedron :... |
 |
|
| 3 | 120 | Rectified dodecahedron (Icosidodecahedron Icosidodecahedron In geometry, an icosidodecahedron is a polyhedron with twenty triangular faces and twelve pentagonal faces. An icosidodecahedron has 30 identical vertices, with two triangles and two pentagons meeting at each, and 60 identical edges, each separating a triangle from a pentagon... ) |
 |
There are 1440 pentagonal faces between the icosidodecahedra
Icosidodecahedron
In geometry, an icosidodecahedron is a polyhedron with twenty triangular faces and twelve pentagonal faces. An icosidodecahedron has 30 identical vertices, with two triangles and two pentagons meeting at each, and 60 identical edges, each separating a triangle from a pentagon...
and pentagonal prism
Pentagonal prism
In geometry, the pentagonal prism is a prism with a pentagonal base. It is a type of heptahedron with 7 faces, 15 edges, and 10 vertices.- As a semiregular polyhedron :...
s. There are 3600 squares between the cuboctahedra
Cuboctahedron
In geometry, a cuboctahedron is a polyhedron with eight triangular faces and six square faces. A cuboctahedron has 12 identical vertices, with two triangles and two squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such it is a quasiregular polyhedron,...
and pentagonal prisms. There are 2400 triangular faces between the icosidodecahedra and cuboctahedra, and 1200 triangular faces between pairs of cuboctahedra.
There are two classes of edges: 3-4-4, 3-4-5: 3600 have two squares and a triangle around it, and 7200 have one triangle, one square, and one pentagon.
Images
| H4 | - |
|---|---|
[30] |
[20] |
| F4 | H3 |
[12] |
[10] |
| A2 / B3 / D4 | A3 / B2 |
[6] |
[4] |
 |
 Stereographic projection Stereographic projection The stereographic projection, in geometry, is a particular mapping that projects a sphere onto a plane. The projection is defined on the entire sphere, except at one point — the projection point. Where it is defined, the mapping is smooth and bijective. It is conformal, meaning that it... with its 3600 green triangular faces and its 3600 blue square faces. |
Cantitruncated 600-cell
| Cantitruncated 600-cell | |
|---|---|
| Type | Uniform polychoron Uniform polychoron In geometry, a uniform polychoron is a polychoron or 4-polytope which is vertex-transitive and whose cells are uniform polyhedra.... |
| Uniform index | 45 |
| Coxeter-Dynkin diagram Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... |
|
| Cells | 1440 total: 120 5.6.6 Truncated icosahedron In geometry, the truncated icosahedron is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids whose faces are two or more types of regular polygons.It has 12 regular pentagonal faces, 20 regular hexagonal faces, 60 vertices and 90 edges.... 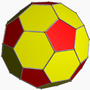 720 4.4.5 Pentagonal prism In geometry, the pentagonal prism is a prism with a pentagonal base. It is a type of heptahedron with 7 faces, 15 edges, and 10 vertices.- As a semiregular polyhedron :...  600 4.6.6 Truncated octahedron In geometry, the truncated octahedron is an Archimedean solid. It has 14 faces , 36 edges, and 24 vertices. Since each of its faces has point symmetry the truncated octahedron is a zonohedron....  |
| Faces | 8640: 3600{4}+1440{5}+ 3600{6} |
| Edges | 14400 |
| Vertices | 7200 |
| Vertex figure Vertex figure In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:... |
 sphenoid Sphenoid Sphenoid may refer to:* In anatomy, the sphenoid bone* In geometry, a tetrahedron with mirror symmetry... |
| Schläfli symbol | t0,1,2{3,3,5} |
| Symmetry group Coxeter group In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example... |
H4, [3,3,5] |
| Properties | convex Convex polytope A convex polytope is a special case of a polytope, having the additional property that it is also a convex set of points in the n-dimensional space Rn... |
The cantitruncated 600-cell is a uniform polychoron
Uniform polychoron
In geometry, a uniform polychoron is a polychoron or 4-polytope which is vertex-transitive and whose cells are uniform polyhedra....
. It is composed of 1440 cells: 120 rhombicosidodecahedron
Rhombicosidodecahedron
In geometry, the rhombicosidodecahedron, or small rhombicosidodecahedron, is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids constructed of two or more types of regular polygon faces....
, 600 truncated tetrahedra
Truncated tetrahedron
In geometry, the truncated tetrahedron is an Archimedean solid. It has 4 regular hexagonal faces, 4 regular triangular faces, 12 vertices and 18 edges.- Area and volume :...
, 720 pentagonal prism
Pentagonal prism
In geometry, the pentagonal prism is a prism with a pentagonal base. It is a type of heptahedron with 7 faces, 15 edges, and 10 vertices.- As a semiregular polyhedron :...
s, and 1200 hexagonal prism
Hexagonal prism
In geometry, the hexagonal prism is a prism with hexagonal base. The shape has 8 faces, 18 edges, and 12 vertices.Since it has eight faces, it is an octahedron. However, the term octahedron is primarily used to refer to the regular octahedron, which has eight triangular faces...
s. It has 7200 vertices, 14400 edges, and 8640 faces (3600 squares, 1440 pentagons, and 3600 hexagons). It has an irregular tetrahedral vertex figure
Vertex figure
In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...
, filled by two truncated tetrahedra, one rhombicosidodecahedron, and one hexagonal prism.
Alternative names
- Cantitruncated 600-cell Norman Johnson
- Cantitruncated hexacosichoron / Cantitruncated polydodecahedron
- great rhombated hexacosachoron (Acronym grix) (George OlshevskyGeorge OlshevskyGeorge Olshevsky is a freelance editor, writer, publisher, amateur paleontologist, and mathematician living in San Diego, California.Olshevsky maintains the comprehensive online Dinosaur Genera List...
and Jonthan Bowers) - Ambo-012 polydodecahedron (John ConwayJohn ConwayJohn Conway may refer to:* John Horton Conway, mathematician at Princeton University. Popularly known for Conway's Game of Life* John B. Conway, mathematician, functional analyst, George Washington University...
)
Images
 Schlegel diagram |
| H3 | A2 / B3 / D4 |
|---|---|
[10] |
[6] |
External links
- Four-Dimensional Polytope Projection Barn Raisings (A Zometool construction of the cantitruncated 120-cell), George W. HartGeorge W. HartGeorge William Hart is a geometer who expresses himself both artistically and academically. He is also a research professor in the department of computer science at the State University of New York in Stony Brook, New York....
- Renaissance Banff 2005 Zome Project: a ZomeZomeThe term zome is used in several related senses. A zome in the original sense is a building using unusual geometries ....
model of a 3D orthogonal projection of the cantellated 600-cell.

