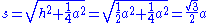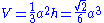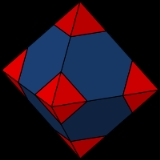
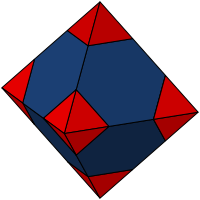
Truncated octahedron
Encyclopedia
In geometry
, the truncated octahedron is an Archimedean solid
. It has 14 faces (8 regular hexagonal and 6 square
), 36 edges, and 24 vertices. Since each of its faces has point symmetry the truncated octahedron is a zonohedron
.
If the original truncated octahedron has unit edge length, its dual tetrakis cube has edge lengths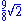 and
and 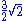 .
.
A truncated octahedron is constructed from a regular octahedron
with side length 3a by the removal of six right square pyramid
s, one from each point. These pyramids have both base side length (a) and lateral side length (e) of a, to form equilateral triangles. The base area is then a². Note that this shape is exactly similar to half an octahedron or Johnson solid
J1.
From the properties of square pyramids, we can now find the slant height, s, and the height, h of the pyramid:
The volume, V, of the pyramid is given by:
Because six pyramids are removed by truncation, there is a total lost volume of √2 a³.
s of (0, ±1, ±2) are Cartesian coordinates of the vertices
of a truncated
octahedron
centered at the origin. The vertices are thus also the corners of 12 rectangles whose long edges are parallel to the coordinate axes.
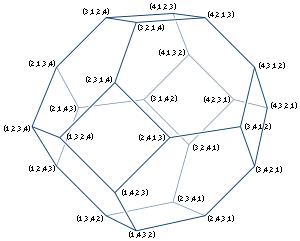
The truncated octahedron can also be represented by even more symmetric coordinates in four dimensions: all permutations of (1,2,3,4) form the vertices of a truncated octahedron in the three-dimensional subspace x + y + z + w = 10. Therefore, the truncated octahedron is the permutohedron
of order 4.
V of a truncated octahedron of edge length a are: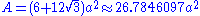
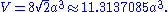
s, with tetrahedral symmetry
and octahedral symmetry
:
and octahedron
:
It also exists as the omnitruncate of the tetrahedron family:
s (space-filling tessellations
):
The cell-transitive bitruncated cubic honeycomb
can also be seen as the Voronoi tessellation of the body-centred cubic lattice
.
The truncated octahedron is one of five three-dimensional primary parallelohedron.
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, the truncated octahedron is an Archimedean solid
Archimedean solid
In geometry an Archimedean solid is a highly symmetric, semi-regular convex polyhedron composed of two or more types of regular polygons meeting in identical vertices...
. It has 14 faces (8 regular hexagonal and 6 square
Square (geometry)
In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles...
), 36 edges, and 24 vertices. Since each of its faces has point symmetry the truncated octahedron is a zonohedron
Zonohedron
A zonohedron is a convex polyhedron where every face is a polygon with point symmetry or, equivalently, symmetry under rotations through 180°. Any zonohedron may equivalently be described as the Minkowski sum of a set of line segments in three-dimensional space, or as the three-dimensional...
.
If the original truncated octahedron has unit edge length, its dual tetrakis cube has edge lengths
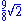 and
and 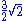 .
.Construction
 |
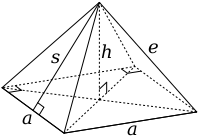 |
A truncated octahedron is constructed from a regular octahedron
Octahedron
In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....
with side length 3a by the removal of six right square pyramid
Square pyramid
In geometry, a square pyramid is a pyramid having a square base. If the apex is perpendicularly above the center of the square, it will have C4v symmetry.- Johnson solid :...
s, one from each point. These pyramids have both base side length (a) and lateral side length (e) of a, to form equilateral triangles. The base area is then a². Note that this shape is exactly similar to half an octahedron or Johnson solid
Johnson solid
In geometry, a Johnson solid is a strictly convex polyhedron, each face of which is a regular polygon, but which is not uniform, i.e., not a Platonic solid, Archimedean solid, prism or antiprism. There is no requirement that each face must be the same polygon, or that the same polygons join around...
J1.
From the properties of square pyramids, we can now find the slant height, s, and the height, h of the pyramid:
The volume, V, of the pyramid is given by:
Because six pyramids are removed by truncation, there is a total lost volume of √2 a³.
Images
Coordinates and permutohedron
All permutationPermutation
In mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
s of (0, ±1, ±2) are Cartesian coordinates of the vertices
Vertex (geometry)
In geometry, a vertex is a special kind of point that describes the corners or intersections of geometric shapes.-Of an angle:...
of a truncated
Truncation (geometry)
In geometry, a truncation is an operation in any dimension that cuts polytope vertices, creating a new facet in place of each vertex.- Uniform truncation :...
octahedron
Octahedron
In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....
centered at the origin. The vertices are thus also the corners of 12 rectangles whose long edges are parallel to the coordinate axes.
The truncated octahedron can also be represented by even more symmetric coordinates in four dimensions: all permutations of (1,2,3,4) form the vertices of a truncated octahedron in the three-dimensional subspace x + y + z + w = 10. Therefore, the truncated octahedron is the permutohedron
Permutohedron
In mathematics, the permutohedron of order n is an -dimensional polytope embedded in an n-dimensional space, the vertices of which are formed by permuting the coordinates of the vector .-History:According to , permutohedra were first studied by...
of order 4.

Area and volume
The area A and the volumeVolume
Volume is the quantity of three-dimensional space enclosed by some closed boundary, for example, the space that a substance or shape occupies or contains....
V of a truncated octahedron of edge length a are:
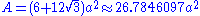
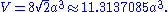
Uniform colorings
There are two uniform coloringUniform coloring
In geometry, a uniform coloring is a property of a uniform figure that is colored to be vertex-transitive...
s, with tetrahedral symmetry
Tetrahedral symmetry
150px|right|thumb|A regular [[tetrahedron]], an example of a solid with full tetrahedral symmetryA regular tetrahedron has 12 rotational symmetries, and a symmetry order of 24 including transformations that combine a reflection and a rotation.The group of all symmetries is isomorphic to the group...
and octahedral symmetry
Octahedral symmetry
150px|thumb|right|The [[cube]] is the most common shape with octahedral symmetryA regular octahedron has 24 rotational symmetries, and a symmetry order of 48 including transformations that combine a reflection and a rotation...
:
| Octahedral symmetry Octahedral symmetry 150px|thumb|right|The [[cube]] is the most common shape with octahedral symmetryA regular octahedron has 24 rotational symmetries, and a symmetry order of 48 including transformations that combine a reflection and a rotation... |
Tetrahedral symmetry Tetrahedral symmetry 150px|right|thumb|A regular [[tetrahedron]], an example of a solid with full tetrahedral symmetryA regular tetrahedron has 12 rotational symmetries, and a symmetry order of 24 including transformations that combine a reflection and a rotation.The group of all symmetries is isomorphic to the group... (Omnitruncated tetrahedron) |
|---|---|
Related polyhedra
The truncated octahedron exists within the set of truncated forms between a cubeCube
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and...
and octahedron
Octahedron
In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....
:
 Cube Cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and... |
 Truncated cube Truncated cube In geometry, the truncated cube, or truncated hexahedron, is an Archimedean solid. It has 14 regular faces , 36 edges, and 24 vertices.... |
 cuboctahedron Cuboctahedron In geometry, a cuboctahedron is a polyhedron with eight triangular faces and six square faces. A cuboctahedron has 12 identical vertices, with two triangles and two squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such it is a quasiregular polyhedron,... |
 Truncated octahedron |
 Octahedron Octahedron In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex.... |
It also exists as the omnitruncate of the tetrahedron family:
 Tetrahedron Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids... |
 Truncated tetrahedron Truncated tetrahedron In geometry, the truncated tetrahedron is an Archimedean solid. It has 4 regular hexagonal faces, 4 regular triangular faces, 12 vertices and 18 edges.- Area and volume :... |
 Rectified tetrahedron Octahedron In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex.... |
 Cantellated tetrahedron Cuboctahedron In geometry, a cuboctahedron is a polyhedron with eight triangular faces and six square faces. A cuboctahedron has 12 identical vertices, with two triangles and two squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such it is a quasiregular polyhedron,... |
 Omnitruncated tetrahedron |
 Snub tetrahedron Icosahedron In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids.... |
Tessellations
The truncated octahedron exists in three different convex uniform honeycombConvex uniform honeycomb
In geometry, a convex uniform honeycomb is a uniform tessellation which fills three-dimensional Euclidean space with non-overlapping convex uniform polyhedral cells.Twenty-eight such honeycombs exist:* the familiar cubic honeycomb and 7 truncations thereof;...
s (space-filling tessellations
Honeycomb (geometry)
In geometry, a honeycomb is a space filling or close packing of polyhedral or higher-dimensional cells, so that there are no gaps. It is an example of the more general mathematical tiling or tessellation in any number of dimensions....
):
| Bitruncated cubic Bitruncated cubic honeycomb The bitruncated cubic honeycomb is a space-filling tessellation in Euclidean 3-space made up of truncated octahedra.It is one of 28 uniform honeycombs. It has 4 truncated octahedra around each vertex.... |
Cantitruncated cubic Cantitruncated cubic honeycomb The cantitruncated cubic honeycomb is a uniform space-filling tessellation in Euclidean 3-space, made up of truncated cuboctahedra, truncated octahedra, and cubes in a ratio of 1:1:3.- Uniform colorings :... |
Truncated alternated cubic Truncated alternated cubic honeycomb The truncated alternated cubic honeycomb is a uniform space-filling tessellation in Euclidean 3-space. It is composed of truncated octahedra, cuboctahedra and truncated tetrahedra in a ratio of 1:1:2. Its vertex figure is a rectangular pyramid.... |
|---|---|---|
 |
 |
 |
The cell-transitive bitruncated cubic honeycomb
Bitruncated cubic honeycomb
The bitruncated cubic honeycomb is a space-filling tessellation in Euclidean 3-space made up of truncated octahedra.It is one of 28 uniform honeycombs. It has 4 truncated octahedra around each vertex....
can also be seen as the Voronoi tessellation of the body-centred cubic lattice
Crystal structure
In mineralogy and crystallography, crystal structure is a unique arrangement of atoms or molecules in a crystalline liquid or solid. A crystal structure is composed of a pattern, a set of atoms arranged in a particular way, and a lattice exhibiting long-range order and symmetry...
.
The truncated octahedron is one of five three-dimensional primary parallelohedron.