Permutohedron
Encyclopedia
In mathematics
, the permutohedron of order n (also spelled permutahedron) is an (n − 1)-dimensional polytope
embedded in an n-dimensional space, the vertices of which are formed by permuting
the coordinates of the vector (1, 2, 3, ..., n).
The alternative spelling permutahedron is sometimes also used. Permutohedra are sometimes also called permutation polytopes, but this terminology is also used for a related polytope, the Birkhoff polytope, defined as the convex hull of permutation matrices
. More generally, uses the phrase "permutation polytope" for any polytope whose vertices are in 1-1 correspondence
with the permutations of some set.
, and connects two vertices that differ by swapping two coordinates the values of which differ by one.
The permutohedron has one facet
for each nonempty proper subset S of {1, 2, 3, ..., n}, consisting of the vertices in which all coordinates in positions in S are smaller than all coordinates in positions not in S. Thus, the total number of facets is 2n − 2. More generally, the faces of the permutohedron (including the permutohedron itself, but not including the empty set) are in 1-1 correspondence with the strict weak ordering
s on a set of n items: a face of dimension d corresponds to a strict weak ordering in which there are n − d equivalence classes.
: the symmetric group
Sn acts
on the permutohedron by permutation of coordinates.
The permutohedron is a zonotope; a translated copy of the permutohedron can be generated as the Minkowski sum of the n(n − 1)/2
line segments that connect the pairs of the standard basis
vectors .
The vertices and edges of the permutohedron are isomorphic
as an undirected graph to one of the Cayley graph
s of the symmetric group
: The Cayley graph generated
by the adjacent transpositions in the symmetric group (transpositions that swap consecutive elements). The Cayley graph of S
4, shown on the right, is generated by the transpositions (1,2), (2,3), and (3,4)
.
The Cayley graph labeling can be constructed by labeling each vertex by the inverse of the permutation given by its coordinates.
This Cayley graph is Hamiltonian; a Hamiltonian cycle may be found by the Steinhaus–Johnson–Trotter algorithm.
 The permutohedron of order n lies entirely in the (n − 1)-dimensional hyperplane consisting of all points whose coordinates sum to the number
The permutohedron of order n lies entirely in the (n − 1)-dimensional hyperplane consisting of all points whose coordinates sum to the number
Moreover, this hyperplane can be tiled
by infinitely many translated
copies of the permutohedron. Each of them differs from the basic permutohedron by an element of a certain (n − 1)-dimensional lattice
, which consists of the n-tuples of integers that sum to zero and whose residues
(modulo n) are all equal:
Thus, the permutohedron of order 4 shown above tiles the 3-dimensional space by translation. Here the 3-dimensional space is the affine subspace of the 4-dimensional space R4 with coordinates x, y, z, w that consists of the 4-tuples of real numbers whose sum is 10,
One easily checks that for each of the following four vectors,
the sum of the coordinates is zero and all coordinates are congruent to 1 (mod 4). Any three of these vectors generate
the translation lattice.
The tessellations formed in this way from the order-2, order-3, and order-4 permutohedra, respectively, are the apeirogon
, the regular hexagonal tiling, and the bitruncated cubic honeycomb
. The dual tessellations contain all simplex
facets, although they are not regular polytopes beyond order-3.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the permutohedron of order n (also spelled permutahedron) is an (n − 1)-dimensional polytope
Polytope
In elementary geometry, a polytope is a geometric object with flat sides, which exists in any general number of dimensions. A polygon is a polytope in two dimensions, a polyhedron in three dimensions, and so on in higher dimensions...
embedded in an n-dimensional space, the vertices of which are formed by permuting
Permutation
In mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
the coordinates of the vector (1, 2, 3, ..., n).
History
According to , permutohedra were first studied by . The name "permutohedron" (or rather its French version, "permutoèdre") was coined by . Regarding this coinage, they write that the word "permutohedron" is barbaric, but easy to remember, and that they submit it to the criticism of their readers.The alternative spelling permutahedron is sometimes also used. Permutohedra are sometimes also called permutation polytopes, but this terminology is also used for a related polytope, the Birkhoff polytope, defined as the convex hull of permutation matrices
Permutation matrix
In mathematics, in matrix theory, a permutation matrix is a square binary matrix that has exactly one entry 1 in each row and each column and 0s elsewhere...
. More generally, uses the phrase "permutation polytope" for any polytope whose vertices are in 1-1 correspondence
Bijection
A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
with the permutations of some set.
Vertices, edges, and facets
The permutohedron of order n has n! vertices, each of which is adjacent to n − 1 others, so the total number of edges is (n − 1)n!/2. Each edge has length √2Square root of 2
The square root of 2, often known as root 2, is the positive algebraic number that, when multiplied by itself, gives the number 2. It is more precisely called the principal square root of 2, to distinguish it from the negative number with the same property.Geometrically the square root of 2 is the...
, and connects two vertices that differ by swapping two coordinates the values of which differ by one.
The permutohedron has one facet
Facet (mathematics)
A facet of a simplicial complex is a maximal simplex.In the general theory of polyhedra and polytopes, two conflicting meanings are currently jostling for acceptability:...
for each nonempty proper subset S of {1, 2, 3, ..., n}, consisting of the vertices in which all coordinates in positions in S are smaller than all coordinates in positions not in S. Thus, the total number of facets is 2n − 2. More generally, the faces of the permutohedron (including the permutohedron itself, but not including the empty set) are in 1-1 correspondence with the strict weak ordering
Strict weak ordering
In mathematics, especially order theory, a strict weak ordering is a binary relation In mathematics, especially order theory, a strict weak ordering is a binary relation ...
s on a set of n items: a face of dimension d corresponds to a strict weak ordering in which there are n − d equivalence classes.
Other properties
The permutohedron is vertex-transitiveVertex-transitive
In geometry, a polytope is isogonal or vertex-transitive if, loosely speaking, all its vertices are the same...
: the symmetric group
Symmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
Sn acts
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
on the permutohedron by permutation of coordinates.
The permutohedron is a zonotope; a translated copy of the permutohedron can be generated as the Minkowski sum of the n(n − 1)/2
Triangular number
A triangular number or triangle number numbers the objects that can form an equilateral triangle, as in the diagram on the right. The nth triangle number is the number of dots in a triangle with n dots on a side; it is the sum of the n natural numbers from 1 to n...
line segments that connect the pairs of the standard basis
Standard basis
In mathematics, the standard basis for a Euclidean space consists of one unit vector pointing in the direction of each axis of the Cartesian coordinate system...
vectors .
The vertices and edges of the permutohedron are isomorphic
Graph isomorphism
In graph theory, an isomorphism of graphs G and H is a bijection between the vertex sets of G and H f \colon V \to V \,\!such that any two vertices u and v of G are adjacent in G if and only if ƒ and ƒ are adjacent in H...
as an undirected graph to one of the Cayley graph
Cayley graph
In mathematics, a Cayley graph, also known as a Cayley colour graph, Cayley diagram, group diagram, or colour group is a graph that encodes the abstract structure of a group. Its definition is suggested by Cayley's theorem and uses a specified, usually finite, set of generators for the group...
s of the symmetric group
Symmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
: The Cayley graph generated
Generating set of a group
In abstract algebra, a generating set of a group is a subset that is not contained in any proper subgroup of the group. Equivalently, a generating set of a group is a subset such that every element of the group can be expressed as the combination of finitely many elements of the subset and their...
by the adjacent transpositions in the symmetric group (transpositions that swap consecutive elements). The Cayley graph of S
Symmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
4, shown on the right, is generated by the transpositions (1,2), (2,3), and (3,4)
Cycle notation
In combinatorial mathematics, the cycle notation is a useful convention for writing down a permutation in terms of its constituent cycles. This is also called circular notation and the permutation called a cyclic or circular permutation....
.
The Cayley graph labeling can be constructed by labeling each vertex by the inverse of the permutation given by its coordinates.
This Cayley graph is Hamiltonian; a Hamiltonian cycle may be found by the Steinhaus–Johnson–Trotter algorithm.
Tessellation of the space

- 1 + 2 + … + n = n(n + 1)/2.
Moreover, this hyperplane can be tiled
Tessellation
A tessellation or tiling of the plane is a pattern of plane figures that fills the plane with no overlaps and no gaps. One may also speak of tessellations of parts of the plane or of other surfaces. Generalizations to higher dimensions are also possible. Tessellations frequently appeared in the art...
by infinitely many translated
Translation (geometry)
In Euclidean geometry, a translation moves every point a constant distance in a specified direction. A translation can be described as a rigid motion, other rigid motions include rotations and reflections. A translation can also be interpreted as the addition of a constant vector to every point, or...
copies of the permutohedron. Each of them differs from the basic permutohedron by an element of a certain (n − 1)-dimensional lattice
Lattice (group)
In mathematics, especially in geometry and group theory, a lattice in Rn is a discrete subgroup of Rn which spans the real vector space Rn. Every lattice in Rn can be generated from a basis for the vector space by forming all linear combinations with integer coefficients...
, which consists of the n-tuples of integers that sum to zero and whose residues
Modular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
(modulo n) are all equal:
- x1 + x2 + … + xn = 0, x1 ≡ x2 ≡ … ≡ xn (mod n).
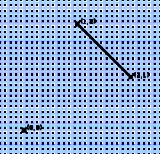
Thus, the permutohedron of order 4 shown above tiles the 3-dimensional space by translation. Here the 3-dimensional space is the affine subspace of the 4-dimensional space R4 with coordinates x, y, z, w that consists of the 4-tuples of real numbers whose sum is 10,
- x + y + z + w = 10.
One easily checks that for each of the following four vectors,
- (1,1,1,−3), (1,1,−3,1), (1,−3,1,1) and (−3,1,1,1),
the sum of the coordinates is zero and all coordinates are congruent to 1 (mod 4). Any three of these vectors generate
Generating set of a group
In abstract algebra, a generating set of a group is a subset that is not contained in any proper subgroup of the group. Equivalently, a generating set of a group is a subset such that every element of the group can be expressed as the combination of finitely many elements of the subset and their...
the translation lattice.
The tessellations formed in this way from the order-2, order-3, and order-4 permutohedra, respectively, are the apeirogon
Apeirogon
An apeirogon is a degenerate polygon with a countably infinite number of sides. It is the limit of a sequence of polygons with more and more sides.Like any polygon, it is a sequence of line segments and angles...
, the regular hexagonal tiling, and the bitruncated cubic honeycomb
Bitruncated cubic honeycomb
The bitruncated cubic honeycomb is a space-filling tessellation in Euclidean 3-space made up of truncated octahedra.It is one of 28 uniform honeycombs. It has 4 truncated octahedra around each vertex....
. The dual tessellations contain all simplex
Simplex
In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...
facets, although they are not regular polytopes beyond order-3.
Gallery
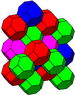
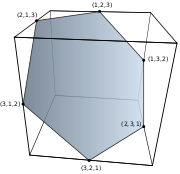
| Order 2 | Order 3 | Order 4 |
|---|---|---|
| 2 vertices | 6 vertices | 24 vertices |
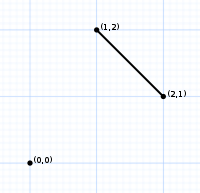 |
 |
|
| The permutohedron of order 2 is a line segment Line segment In geometry, a line segment is a part of a line that is bounded by two end points, and contains every point on the line between its end points. Examples of line segments include the sides of a triangle or square. More generally, when the end points are both vertices of a polygon, the line segment... on the diagonal of a unit square Unit square In mathematics, a unit square is a square whose sides have length 1. Often, "the" unit square refers specifically to the square in the Cartesian plane with corners at , , , and .-In the real plane:... . |
The permutohedron of order 3 is a hexagon, filling the cross section of a 2×2×2 cube Cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and... . |
The permutohedron of order 4 forms a truncated octahedron Truncated octahedron In geometry, the truncated octahedron is an Archimedean solid. It has 14 faces , 36 edges, and 24 vertices. Since each of its faces has point symmetry the truncated octahedron is a zonohedron.... . |
| Order 5 | Order 6 |
|---|---|
| 120 vertices | 720 vertices |
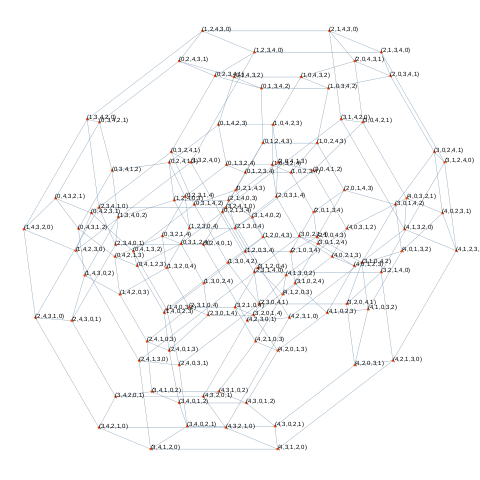 |
 |
| The permutohedron of order 5 forms an omnitruncated 5-cell. | The permutohedron of order 6 forms an omnitruncated 5-simplex. |

