Transposition (mathematics)
Encyclopedia
In informal language, a transposition is a function that swaps two elements of a set. More formally, given a finite set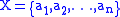 
, a transposition is a permutation
(bijective function
of
onto itself) 
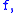such that there exist indices 
with 
such that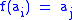 
, 
and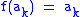 
for all other indices 
This is often denoted (in the cycle notation
) as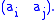
For example, if
, the function
given by
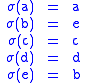
is a transposition.
(product) of transpositions—formally, they are generators
for the group
. In fact, if one takes
, 
, ..., 
, then any permutation can be expressed as a product of , meaning the transpositions 
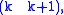in this case 
, 
, 
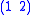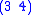, and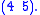 
This follows because an arbitrary transposition can be expressed as the product of adjacent transpositions. Concretely, one can express the transposition 
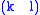where 
by moving k to l one step at a time, then moving l back to where k was, which interchanges these two and makes no other changes:
In fact, the symmetric group
is a Coxeter group
, meaning that it is generated by elements of order 2 (the adjacent transpositions), and all relations are of a certain form.
One of the main results on symmetric groups states that either all of the decompositions of a given permutation into transpositions have an even number of transpositions, or they all have an odd number of transpositions, that allows to define the parity of a permutation.
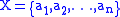, a transposition is a permutationPermutation
In mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
(bijective function
Bijection
A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
of
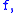onto itself) such that there exist indices with such that 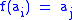, and 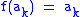for all other indices This is often denoted (in the cycle notationCycle notation
In combinatorial mathematics, the cycle notation is a useful convention for writing down a permutation in terms of its constituent cycles. This is also called circular notation and the permutation called a cyclic or circular permutation....
) as
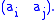
For example, if
, the functionFunction (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
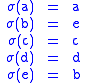
given byis a transposition.
Properties
Any permutation can be expressed as the compositionFunction composition
In mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
(product) of transpositions—formally, they are generators
Generating set of a group
In abstract algebra, a generating set of a group is a subset that is not contained in any proper subgroup of the group. Equivalently, a generating set of a group is a subset such that every element of the group can be expressed as the combination of finitely many elements of the subset and their...
for the group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
. In fact, if one takes
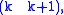, , ..., , then any permutation can be expressed as a product of , meaning the transpositions in this case 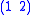, , , 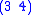and 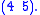This follows because an arbitrary transposition can be expressed as the product of adjacent transpositions. Concretely, one can express the transposition 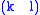where by moving k to l one step at a time, then moving l back to where k was, which interchanges these two and makes no other changes:In fact, the symmetric group
Symmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
is a Coxeter group
Coxeter group
In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example...
, meaning that it is generated by elements of order 2 (the adjacent transpositions), and all relations are of a certain form.
One of the main results on symmetric groups states that either all of the decompositions of a given permutation into transpositions have an even number of transpositions, or they all have an odd number of transpositions, that allows to define the parity of a permutation.
External links
See also
- Cycle (mathematics)Cycle (mathematics)In mathematics, and in particular in group theory, a cycle is a permutation of the elements of some set X which maps the elements of some subset S to each other in a cyclic fashion, while fixing all other elements...
- Signature of a permutation