Cycle (mathematics)
Encyclopedia
In mathematics
, and in particular in group theory
, a cycle is a permutation
of the elements of some set X which maps the elements of some subset S to each other in a cyclic fashion, while fixing (i.e., mapping to themselves) all other elements. The set S is called the orbit of the cycle.
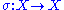, is called a cycle if the action on X of the subgroup generated by 
has exactly one orbit with more than a single element. This notion is most commonly used when X is a finite set; then of course the orbit S in question is also finite. Let 
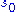be any element of S, and put 
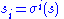for any 
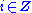. Since by assumption S has more than one element, 
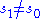; if S is finite, there is a minimal number 
for which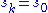 
. Then 
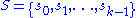, and 
is the permutation defined by
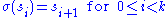
and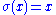
for any element of 
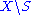. The elements not fixed by 
can be pictured as
.
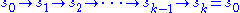A cycle can be written using the compact cycle notation
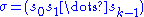(there are no commas between elements in this notation, to avoid confusion with a k-tuple
). The length of a cycle, is the number of elements of its orbit of non-fixed elements. A cycle of length k is also called a k-cycle.
s says that any permutation can be expressed as the product of disjoint cycles (more precisely: cycles with disjoint orbits); such cycles commute with each other, and the expression of the permutation is unique up to the order of the cycles (but note that the cycle notation is not unique: each k-cycle can itself be written in k different ways, depending on the choice of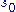
in its orbit). The multiset
of lengths of the cycles in this expression is therefore uniquely determined by the permutation, and both the signature and the conjugacy class
of the permutation in the symmetric group are determined by it.
The number of k-cycles in the symmetric group Sn is given, for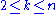
, by the following equivalent formulas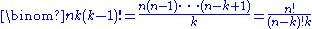
A k-cycle has signature (−1)k − 1.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, and in particular in group theory
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
, a cycle is a permutation
Permutation
In mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
of the elements of some set X which maps the elements of some subset S to each other in a cyclic fashion, while fixing (i.e., mapping to themselves) all other elements. The set S is called the orbit of the cycle.
Definition
A permutation of a set X, which is a bijective functionBijection
A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
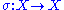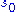, is called a cycle if the action on X of the subgroup generated by has exactly one orbit with more than a single element. This notion is most commonly used when X is a finite set; then of course the orbit S in question is also finite. Let be any element of S, and put 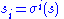for any 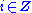. Since by assumption S has more than one element, 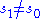; if S is finite, there is a minimal number for which 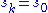. Then 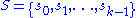, and is the permutation defined by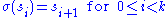and
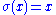for any element of 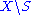. The elements not fixed by can be pictured as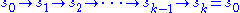.A cycle can be written using the compact cycle notation
Cycle notation
In combinatorial mathematics, the cycle notation is a useful convention for writing down a permutation in terms of its constituent cycles. This is also called circular notation and the permutation called a cyclic or circular permutation....
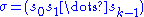(there are no commas between elements in this notation, to avoid confusion with a k-tupleTuple
In mathematics and computer science, a tuple is an ordered list of elements. In set theory, an n-tuple is a sequence of n elements, where n is a positive integer. There is also one 0-tuple, an empty sequence. An n-tuple is defined inductively using the construction of an ordered pair...
). The length of a cycle, is the number of elements of its orbit of non-fixed elements. A cycle of length k is also called a k-cycle.
Basic properties
One of the basic results on symmetric groupSymmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
s says that any permutation can be expressed as the product of disjoint cycles (more precisely: cycles with disjoint orbits); such cycles commute with each other, and the expression of the permutation is unique up to the order of the cycles (but note that the cycle notation is not unique: each k-cycle can itself be written in k different ways, depending on the choice of
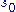in its orbit). The multisetMultiset
In mathematics, the notion of multiset is a generalization of the notion of set in which members are allowed to appear more than once...
of lengths of the cycles in this expression is therefore uniquely determined by the permutation, and both the signature and the conjugacy class
Conjugacy class
In mathematics, especially group theory, the elements of any group may be partitioned into conjugacy classes; members of the same conjugacy class share many properties, and study of conjugacy classes of non-abelian groups reveals many important features of their structure...
of the permutation in the symmetric group are determined by it.
The number of k-cycles in the symmetric group Sn is given, for
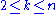, by the following equivalent formulas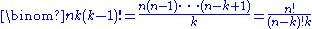A k-cycle has signature (−1)k − 1.
See also
- Cycles and fixed points
- fifteen puzzle
- symmetric groupSymmetric groupIn mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
- transposition
- groupGroup (mathematics)In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
- subgroupSubgroupIn group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
- dihedral groupDihedral groupIn mathematics, a dihedral group is the group of symmetries of a regular polygon, including both rotations and reflections. Dihedral groups are among the simplest examples of finite groups, and they play an important role in group theory, geometry, and chemistry.See also: Dihedral symmetry in three...
- cycle detection