Zome
Encyclopedia
The term zome is used in several related senses. A zome in the original sense is a building using unusual geometries (different from the standard house or other building which is essentially one or a series of rectangular boxes).
The word "zome" was coined in 1968 by Steve Durkee, now known as Nooruddeen Durkee
, combining the words "dome" and "zonahedron." One of the earliest models ended up as a large climbing structure at the Lama Foundation
.
In the second sense as a learning tool or toy, "Zometool" refers to a model-construction toy manufactured by Zometool, Inc.. It is sometimes thought of as the ultimate form of the "ball and stick" construction toy, in form. It appeals to adults as well as children, and is educational on many levels (not the least, geometry). Finally, the term "Zome system" refers to the mathematics underlying the physical construction system.
Both the building and the learning tool are the brainchildren of inventor/designer Steve Baer
, his wife, Holly, and associates.
s) other than rectangular ones. Baer and his wife, Holly, moved back to the U.S., settling in Albuquerque, New Mexico
in the early 1960s. In New Mexico, he experimented with constructing buildings of unusual geometries (calling them by his friend Steve Durkee's term: "zomes" — see "Drop City
") — buildings intended to be appropriate to their environment, notably to utilize solar energy well. Baer was fascinated with the dome geometry introduced by architect R. Buckminster Fuller
. Baer was an occasional guest at Drop City, an arts and experimental community near Trinidad, CO. He wanted to design and construct buildings that didn't suffer from some of the limitations of the smaller, owner-built versions of geodesic domes (of the 'pure Fuller' design).
In recent years, the unconventional "zome" building-design approach with its
multi-faceted geometric lines has been taken up by French builders in the
Pyrenees. A recent book, Home Work, published in 2004 and edited by Lloyd Kahn
, has a section featuring these buildings. While
many zomes built in the last couple decades have been wood-framed and made use
of wood sheathing, much of what Baer himself originally designed and constructed
involved metal framing with a sheet-metal outer skin.
The Zometool plastic construction set
is produced by a
privately-owned corporation of the same name, based in Denver, Colorado
, and which evolved out
of Baer's company ZomeWorks. It is perhaps best described as a "space-frame
construction set". Its elements consist of small connector nodes
and struts of various colors. The overall shape of a connector node is
that of a non-uniform small rhombicosidodecahedron
, except that each face
is replaced by a small hole. The ends of the struts are designed to
fit in the holes of the connector nodes, allowing for syntheses of
a variety of structures. The idea of shape-coding the three types of struts was developed by Marc Pelletier and Paul Hildebrandt. To create the "balls," or nodes, Pelletier and Hildebrandt invented a system of 62 hydraulic pins that came together to form a mold. The first connector node emerged from their mold perfectly on April 1, 1992. These parts are made from state-of-the-art ABS plastic
injection-mold technology. .
In the years since 1992, Zometool has widened and enriched
its line of products. Much of the development has focused on improving
the style or the variety of struts available. Since 1992, the basic design
of the connector node has not changed, and hence the various parts released
have remained universally compatible. From 1992 until 2000, Zometool
produced many kits which included connector nodes and blue, yellow, and
red struts. In 2000, Zometool introduced green lines, which were designed
to allow the user to build, among other things, models of the regular
tetrahedron and octahedron. In 2003, Zometool
changed the style of the struts slightly. The struts "with clicks"
have a different surface texture and they also have longer nibs which
allow for a more robust connection between connector node and strut.
Characteristics of Zometool
The color of a Zometool strut is associated with its cross
section and also with the shape of the hole of the connector node
in which it fits.
Each blue strut has a rectangular cross section, each yellow strut
has a triangular cross section, and each red strut has a pentagonal cross
section. The cross section of a green strut is a rhombus, where the ratio of
the diagonals is √2. The green struts, fitting
in the "red" pentagonal holes, are not a part
of the 1992 release of Zometool, and, consequently, using them
is not as straightforward as the other colors. One may
find a variety of colors of connector nodes, but these all have the same purpose
and design.
At their midpoints, each of the yellow and red struts has an apparent
twist. At these points, the cross-sectional shape reverses.
This design feature forces the connector nodes on the ends of the strut to have
the same orientation.
Similarly, the cross section of the blue strut is a non-square rectangle,
again ensuring that the two nodes on the ends have the same orientation.
Instead of a twist, the green struts have two bends which allow them to fit
into the pentagonal holes of the connector node.
Among other places, the word Zome comes from the term zone. The Zome system
allows no more than 61 zones. The cross-sectional shapes
correspond to colors, and in turn these correspond to zone colors. Hence the
Zome system has 15 blue zones, 10 yellow zones, 6 red zones, and 30 green zones.
Two shapes are associated with
blue. The blue struts with a rectangular cross section are designed
to lie in the same zones as the blue struts, but they are half the length
of a blue strut; hence these struts are often called "half-blue" (and were originally made in a light blue color).
The blue-green struts with a rhombic cross section lie in the same zones
as the green struts, but they are designed so that the ratio of a rhombic blue-green strut to a blue strut is 1:1 (as opposed to the green strut's √2:1). It is important
to understand that, due to this length ratio, the blue-green struts having a rhombic cross section
do not mathematically belong to the Zome system.
Zometool construction set is based. It is defined in terms of the
vector space
, equipped with the standard inner product,
also known as 3-dimensional Euclidean space.
Let
denote the Golden ratio
and
let
denote the symmetry group of the configuration of
vectors
, 
, and 
.
The group
, an example of a Coxeter group
, is known as the icosahedral group because it is the symmetry
group of a regular icosahedron
having these vectors as its vertices.
Define the "standard blue vectors" as the
-orbit of the vector 
.
Define the "standard yellow vectors" as the
-orbit of the vector 
.
Define the "standard red vectors" as the
-orbit of the vector 
.
A "strut" of the Zome System is any vector which can be obtained from the standard
vectors described above by scaling by any power
, where 
is
an integer. A "node" of the Zome System is any element of the subgroup of
generated by the struts. Finally, the "Zome system" is the set of all pairs
,
where
is a set of nodes and 
is a set of pairs
such that 
and 
are in 
and the difference
is a strut.
One may check that there are 30, 20, and 12 standard vectors having the
colors blue, yellow, and red, respectively. Correspondingly,
the stabilizer subgroup of a blue, yellow, or red strut is isomorphic to the dihedral group of order
4, 6, or 10, respectively. Hence, one may also describe the blue, yellow, and red
struts as "rectangular", "trianglular", and "pentagonal", respectively.
One may extend the Zome system by adjoining green vectors.
The "standard green vectors" comprise the
-orbit of the vector 
.
and a "green strut" as any vector which can be obtained by scaling a standard
green vector by any integral power
. As above, one may check that there
are 60 standard green vectors and that the stabilizer subgroup of such a vector
is a two-element group generated by a reflection symmetry of the regular
icosahedron. One may then enhance the Zome system by including these green struts.
Doing this does not affect the set of nodes.
The abstract Zome system defined above is significant because of the following fact: Every connected Zome model
has a faithful image in the Zome system. The converse of this fact is only partially true,
but this is due only to the laws of physics. For example, the radius of a Zometool node is positive (as opposed to a node being a single point mathematically),
so one cannot make a Zometool model where two nodes are separated by an arbitrarily
small prescribed distance. Similarly, only a finite number of lengths of struts will ever be manufactured, and a green strut cannot be placed directly adjacent to a red strut or another green strut with which it shares the same hole (even though they are mathematically distinct).
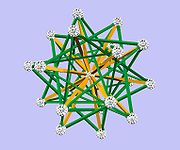The Zome system is especially good at modeling 1-dimensional
skeleta of highly symmetric objects in 3- and
4-dimensional Euclidean space.
The most prominent among these are the five Platonic solids,
and the 4-dimensional polytopes related to the 120-cell and
the 600-cell.
However, the list of mathematical objects which are amenable to
Zome is long, and an exhaustive list is not forthcoming.
Besides those already mentioned, one may use Zome to model the following
mathematical objects:
Other uses include
the study of engineering problems, especially
steel-truss structures,
the study of some molecular
, nanotube
, and viral
structures,
to make soap film surfaces
, and as an artistic medium.
Zome modelling system:
The word "zome" was coined in 1968 by Steve Durkee, now known as Nooruddeen Durkee
Nooruddeen Durkee
Shaykh Abdullah Nooruddeen Durkee is a Muslim scholar, thinker, author, translator and the khalifah for North America of the Shadhdhuli School for Tranquility of Being and the Illumination of Hearts, Green Mountain Branch. Nooruddeen Durkee became a Muslim in his early thirties in al-Quds,...
, combining the words "dome" and "zonahedron." One of the earliest models ended up as a large climbing structure at the Lama Foundation
Lama Foundation
The Lama Foundation is a community in the mountains of New Mexico, seventeen miles north of Taos.-History:The Lama Foundation was founded in 1967 by Barbara Durkee and Stephen Durkee . It began with the purchase of of land adjacent to federal forested land, and continues today as a place for...
.
In the second sense as a learning tool or toy, "Zometool" refers to a model-construction toy manufactured by Zometool, Inc.. It is sometimes thought of as the ultimate form of the "ball and stick" construction toy, in form. It appeals to adults as well as children, and is educational on many levels (not the least, geometry). Finally, the term "Zome system" refers to the mathematics underlying the physical construction system.
Both the building and the learning tool are the brainchildren of inventor/designer Steve Baer
Steve Baer
Steve Baer is an American inventor and solar and residential designer. Baer has served on the board of directors of the U.S. Section of the International Solar Energy Society, and on the board of the New Mexico Solar Energy Association. He is the Founder, Chairman of the Board, President, and...
, his wife, Holly, and associates.
The Zome as Building Concept
Following his education at Amherst College and UCLA, Steve Baer studied mathematics at Eidgenössische Technische Hochschule (Zurich, Switzerland). Here he became interested in the possibilities of building innovative structures using polyhedra (polyhedronPolyhedron
In elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...
s) other than rectangular ones. Baer and his wife, Holly, moved back to the U.S., settling in Albuquerque, New Mexico
New Mexico
New Mexico is a state located in the southwest and western regions of the United States. New Mexico is also usually considered one of the Mountain States. With a population density of 16 per square mile, New Mexico is the sixth-most sparsely inhabited U.S...
in the early 1960s. In New Mexico, he experimented with constructing buildings of unusual geometries (calling them by his friend Steve Durkee's term: "zomes" — see "Drop City
Drop City
Drop City was an artists' community that formed in southern Colorado in 1965. Abandoned by the early 1970s, it became known as the first rural "hippie commune".-Establishment:...
") — buildings intended to be appropriate to their environment, notably to utilize solar energy well. Baer was fascinated with the dome geometry introduced by architect R. Buckminster Fuller
Buckminster Fuller
Richard Buckminster “Bucky” Fuller was an American systems theorist, author, designer, inventor, futurist and second president of Mensa International, the high IQ society....
. Baer was an occasional guest at Drop City, an arts and experimental community near Trinidad, CO. He wanted to design and construct buildings that didn't suffer from some of the limitations of the smaller, owner-built versions of geodesic domes (of the 'pure Fuller' design).
In recent years, the unconventional "zome" building-design approach with its
multi-faceted geometric lines has been taken up by French builders in the
Pyrenees. A recent book, Home Work, published in 2004 and edited by Lloyd Kahn
Lloyd Kahn
Lloyd Kahn is the founding editor-in-chief of Shelter Publications, Inc., and is the former Shelter editor of the Whole Earth Catalog. He is also an author, photographer, and pioneer of the green building and green architecture movements....
, has a section featuring these buildings. While
many zomes built in the last couple decades have been wood-framed and made use
of wood sheathing, much of what Baer himself originally designed and constructed
involved metal framing with a sheet-metal outer skin.
Construction Set
Construction set
A construction set is a set of standardized pieces that allow for the construction of a variety of different models. The pieces avoid the lead time of manufacturing custom pieces, and of requiring special training or design time to construct complex systems...
is produced by a
privately-owned corporation of the same name, based in Denver, Colorado
Denver, Colorado
The City and County of Denver is the capital and the most populous city of the U.S. state of Colorado. Denver is a consolidated city-county, located in the South Platte River Valley on the western edge of the High Plains just east of the Front Range of the Rocky Mountains...
, and which evolved out
of Baer's company ZomeWorks. It is perhaps best described as a "space-frame
construction set". Its elements consist of small connector nodes
and struts of various colors. The overall shape of a connector node is
that of a non-uniform small rhombicosidodecahedron
Rhombicosidodecahedron
In geometry, the rhombicosidodecahedron, or small rhombicosidodecahedron, is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids constructed of two or more types of regular polygon faces....
, except that each face
is replaced by a small hole. The ends of the struts are designed to
fit in the holes of the connector nodes, allowing for syntheses of
a variety of structures. The idea of shape-coding the three types of struts was developed by Marc Pelletier and Paul Hildebrandt. To create the "balls," or nodes, Pelletier and Hildebrandt invented a system of 62 hydraulic pins that came together to form a mold. The first connector node emerged from their mold perfectly on April 1, 1992. These parts are made from state-of-the-art ABS plastic
Acrylonitrile butadiene styrene
Acrylonitrile butadiene styrene is a common thermoplastic. Its melting point is approximately 105 °C ....
injection-mold technology. .
In the years since 1992, Zometool has widened and enriched
its line of products. Much of the development has focused on improving
the style or the variety of struts available. Since 1992, the basic design
of the connector node has not changed, and hence the various parts released
have remained universally compatible. From 1992 until 2000, Zometool
produced many kits which included connector nodes and blue, yellow, and
red struts. In 2000, Zometool introduced green lines, which were designed
to allow the user to build, among other things, models of the regular
tetrahedron and octahedron. In 2003, Zometool
changed the style of the struts slightly. The struts "with clicks"
have a different surface texture and they also have longer nibs which
allow for a more robust connection between connector node and strut.
Characteristics of Zometool
The color of a Zometool strut is associated with its cross
section and also with the shape of the hole of the connector node
in which it fits.
Each blue strut has a rectangular cross section, each yellow strut
has a triangular cross section, and each red strut has a pentagonal cross
section. The cross section of a green strut is a rhombus, where the ratio of
the diagonals is √2. The green struts, fitting
in the "red" pentagonal holes, are not a part
of the 1992 release of Zometool, and, consequently, using them
is not as straightforward as the other colors. One may
find a variety of colors of connector nodes, but these all have the same purpose
and design.
At their midpoints, each of the yellow and red struts has an apparent
twist. At these points, the cross-sectional shape reverses.
This design feature forces the connector nodes on the ends of the strut to have
the same orientation.
Similarly, the cross section of the blue strut is a non-square rectangle,
again ensuring that the two nodes on the ends have the same orientation.
Instead of a twist, the green struts have two bends which allow them to fit
into the pentagonal holes of the connector node.
Among other places, the word Zome comes from the term zone. The Zome system
allows no more than 61 zones. The cross-sectional shapes
correspond to colors, and in turn these correspond to zone colors. Hence the
Zome system has 15 blue zones, 10 yellow zones, 6 red zones, and 30 green zones.
Two shapes are associated with
blue. The blue struts with a rectangular cross section are designed
to lie in the same zones as the blue struts, but they are half the length
of a blue strut; hence these struts are often called "half-blue" (and were originally made in a light blue color).
The blue-green struts with a rhombic cross section lie in the same zones
as the green struts, but they are designed so that the ratio of a rhombic blue-green strut to a blue strut is 1:1 (as opposed to the green strut's √2:1). It is important
to understand that, due to this length ratio, the blue-green struts having a rhombic cross section
do not mathematically belong to the Zome system.
A definition of the Zome system
Here is a mathematical definition of the Zome system, on which the physicalZometool construction set is based. It is defined in terms of the
vector space
, equipped with the standard inner product,also known as 3-dimensional Euclidean space.
Let
denote the Golden ratioGolden ratio
In mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989...
and
let
denote the symmetry group of the configuration ofvectors
, , and .The group
, an example of a Coxeter groupCoxeter group
In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example...
, is known as the icosahedral group because it is the symmetry
group of a regular icosahedron
Icosahedron
In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids....
having these vectors as its vertices.
Define the "standard blue vectors" as the
-orbit of the vector .Define the "standard yellow vectors" as the
-orbit of the vector .Define the "standard red vectors" as the
-orbit of the vector .A "strut" of the Zome System is any vector which can be obtained from the standard
vectors described above by scaling by any power
, where isan integer. A "node" of the Zome System is any element of the subgroup of
generated by the struts. Finally, the "Zome system" is the set of all pairs
,where
is a set of nodes and is a set of pairs such that and are in and the difference
is a strut.One may check that there are 30, 20, and 12 standard vectors having the
colors blue, yellow, and red, respectively. Correspondingly,
the stabilizer subgroup of a blue, yellow, or red strut is isomorphic to the dihedral group of order
4, 6, or 10, respectively. Hence, one may also describe the blue, yellow, and red
struts as "rectangular", "trianglular", and "pentagonal", respectively.
One may extend the Zome system by adjoining green vectors.
The "standard green vectors" comprise the
-orbit of the vector .and a "green strut" as any vector which can be obtained by scaling a standard
green vector by any integral power
. As above, one may check that thereare 60 standard green vectors and that the stabilizer subgroup of such a vector
is a two-element group generated by a reflection symmetry of the regular
icosahedron. One may then enhance the Zome system by including these green struts.
Doing this does not affect the set of nodes.
The abstract Zome system defined above is significant because of the following fact: Every connected Zome model
has a faithful image in the Zome system. The converse of this fact is only partially true,
but this is due only to the laws of physics. For example, the radius of a Zometool node is positive (as opposed to a node being a single point mathematically),
so one cannot make a Zometool model where two nodes are separated by an arbitrarily
small prescribed distance. Similarly, only a finite number of lengths of struts will ever be manufactured, and a green strut cannot be placed directly adjacent to a red strut or another green strut with which it shares the same hole (even though they are mathematically distinct).
Zome as a modeling system
skeleta of highly symmetric objects in 3- and
4-dimensional Euclidean space.
The most prominent among these are the five Platonic solids,
and the 4-dimensional polytopes related to the 120-cell and
the 600-cell.
However, the list of mathematical objects which are amenable to
Zome is long, and an exhaustive list is not forthcoming.
Besides those already mentioned, one may use Zome to model the following
mathematical objects:
- Three of the four Kepler-Poinsot polyhedra
- Regular Polyhedral compoundPolyhedral compoundA polyhedral compound is a polyhedron that is itself composed of several other polyhedra sharing a common centre. They are the three-dimensional analogs of polygonal compounds such as the hexagram....
s - Regular 4-dimensional polytopes and some compounds
- Many stellations of the rhombic triacontahedronRhombic triacontahedronIn geometry, the rhombic triacontahedron is a convex polyhedron with 30 rhombic faces. It is an Archimedean dual solid, or a Catalan solid. It is the polyhedral dual of the icosidodecahedron, and it is a zonohedron....
- Many stellations of the regular icosahedronIcosahedronIn geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids....
- Zonohedra, especially the rhombic enneacontahedronRhombic enneacontahedronA rhombic enneacontahedron is a polyhedron composed of 90 rhombic faces; with three, five, or six rhombi meeting at each vertex. It has 60 broad rhombi and 30 slim...
and rhombic triacontahedronRhombic triacontahedronIn geometry, the rhombic triacontahedron is a convex polyhedron with 30 rhombic faces. It is an Archimedean dual solid, or a Catalan solid. It is the polyhedral dual of the icosidodecahedron, and it is a zonohedron.... - HypercubeHypercubeIn geometry, a hypercube is an n-dimensional analogue of a square and a cube . It is a closed, compact, convex figure whose 1-skeleton consists of groups of opposite parallel line segments aligned in each of the space's dimensions, perpendicular to each other and of the same length.An...
s in dimensions 61 or fewer - Most uniform polyhedraUniform polyhedronA uniform polyhedron is a polyhedron which has regular polygons as faces and is vertex-transitive...
(a major exception being those formed using the snub operation) - Many 4-dimensional uniform polytopesUniform polychoronIn geometry, a uniform polychoron is a polychoron or 4-polytope which is vertex-transitive and whose cells are uniform polyhedra....
- Thorold Gosset's exceptional semiregular polytopesSemiregular E-polytopeIn geometry, a uniform k21 polytope is a polytope in k + 4 dimensions constructed from the En Coxeter group, and having only regular polytope facets...
in 6, 7, and 8 dimensions - A few of the Johnson solidJohnson solidIn geometry, a Johnson solid is a strictly convex polyhedron, each face of which is a regular polygon, but which is not uniform, i.e., not a Platonic solid, Archimedean solid, prism or antiprism. There is no requirement that each face must be the same polygon, or that the same polygons join around...
s - Desargues' configurationDesargues' theoremIn projective geometry, Desargues' theorem, named in honor of Gérard Desargues, states:Denote the three vertices of one triangle by a, b, and c, and those of the other by A, B, and C...
- Two of the Catalan solidCatalan solidIn mathematics, a Catalan solid, or Archimedean dual, is a dual polyhedron to an Archimedean solid. The Catalan solids are named for the Belgian mathematician, Eugène Catalan, who first described them in 1865....
s - Classical and exceptional root systemRoot systemIn mathematics, a root system is a configuration of vectors in a Euclidean space satisfying certain geometrical properties. The concept is fundamental in the theory of Lie groups and Lie algebras...
s - TrialityTrialityIn mathematics, triality is a relationship between three vector spaces, analogous to the duality relation between dual vector spaces. Most commonly, it describes those special features of the Dynkin diagram D4 and the associated Lie group Spin, the double cover of 8-dimensional rotation group SO,...
(from Lie theory)
Other uses of Zome
The uses of Zome are not restricted to pure mathematics.Other uses include
the study of engineering problems, especially
steel-truss structures,
the study of some molecular
Molecule
A molecule is an electrically neutral group of at least two atoms held together by covalent chemical bonds. Molecules are distinguished from ions by their electrical charge...
, nanotube
Nanotube
A nanotube is a nanometer-scale tube-like structure. It may refer to:* Carbon nanotube* Inorganic nanotube* DNA nanotube* Membrane nanotube - a tubular membrane connection between cells...
, and viral
Virus
A virus is a small infectious agent that can replicate only inside the living cells of organisms. Viruses infect all types of organisms, from animals and plants to bacteria and archaea...
structures,
to make soap film surfaces
Minimal surface
In mathematics, a minimal surface is a surface with a mean curvature of zero.These include, but are not limited to, surfaces of minimum area subject to various constraints....
, and as an artistic medium.
External links
Zome buildings:- The zome building concept explained
- Examples of European zome buildings
- Examples of zome usage in North American prefabricated housing construction
Zome modelling system:
- Zometool The manufacturer's site.
- Advanced Zome Projects by David Richter
- Zome Geometry by George W. HartGeorge W. HartGeorge William Hart is a geometer who expresses himself both artistically and academically. He is also a research professor in the department of computer science at the State University of New York in Stony Brook, New York....
and Henri Picciotto - vZome for building virtual Zome models
- Zome at Bridges London at the London Knowledge Lab
- Japan Zome Club a user's club in Japan (Japanese)
- Metazome a project making Zome models with Zome