Semiregular E-polytope - AbsoluteAstronomy.com

In geometry

Geometry

Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....

, a uniform k₂₁ polytope is a polytope

Polytope

In elementary geometry, a polytope is a geometric object with flat sides, which exists in any general number of dimensions. A polygon is a polytope in two dimensions, a polyhedron in three dimensions, and so on in higher dimensions...

in k + 4 dimensions constructed from the E_n

En (Lie algebra)

In mathematics, especially in Lie theory, En is the Kac–Moody algebra whose Dynkin diagram is a bifurcating graph with three branches of length 1,2, and k, with k=n-4....

Coxeter group

In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example...

, and having only regular polytope

Regular polytope

In mathematics, a regular polytope is a polytope whose symmetry is transitive on its flags, thus giving it the highest degree of symmetry. All its elements or j-faces — cells, faces and so on — are also transitive on the symmetries of the polytope, and are regular polytopes of...

facets. The family was named by Coxeter as k₂₁ by its bifurcating Coxeter–Dynkin diagram, with a single ring on the end of the k-node sequence.

Thorold Gosset

Thorold Gosset

Thorold Gosset was an English lawyer and an amateur mathematician. In mathematics, he is noted for discovering and classifying the semiregular polytopes in dimensions four and higher.According to H. S. M...

discovered this family as a part of his 1900 enumeration of the regular and semiregular polytopes, and so they are sometimes called Gosset's semiregular figures. Gosset named them by their dimension from 5 to 9, for example the 5-ic semiregular figure.

Family members

The sequence as identified by Gosset ends as an infinite tessellation (space-filling honeycomb) in 8-space, called the E8 lattice

E8 lattice

In mathematics, the E8 lattice is a special lattice in R8. It can be characterized as the unique positive-definite, even, unimodular lattice of rank 8...

. (A final form was not discovered by Gosset and is called the E9 lattice: 6_{21. It is a tessellation of hyperbolic 9-space constructed of (∞ 9-simplexSimplex
In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...

and ∞ 9-orthoplex facets with all vertices at infinity.)

The family starts uniquely as 6-polytope6-polytope
In six-dimensional geometry, a uniform polypeton is a six-dimensional uniform polytope. A uniform polypeton is vertex-transitive, and all facets are uniform polytera....

s. The triangular prism and rectified 5-cell are included at the beginning for completeness. The demipenteract also exists in the demihypercube family.

They are also sometimes named by their symmetry group, like E6 polytope, although there are many uniform polytopeUniform polytope
A uniform polytope is a vertex-transitive polytope made from uniform polytope facets of a lower dimension. Uniform polytopes of 2 dimensions are the regular polygons....

s within the E₆ symmetry.

The complete family of Gosset semiregular polytopes are:

triangular prismTriangular prism
In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides....

: −1_{21 (2 triangleTriangle
A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....

s and 3 squareSquare (geometry)
In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles...

faces)}
rectified 5-cellRectified 5-cell
In four dimensional geometry, the rectified 5-cell is a uniform polychoron composed of 5 regular tetrahedral and 5 regular octahedral cells. Each edge has one tetrahedron and two octahedra. Each vertex has two tetrahedra and three octahedra. In total it has 30 triangle faces, 30 edges, and 10...

: 0_{21, Tetroctahedric (5 tetrahedraTetrahedron
In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...

and 5 octahedraOctahedron
In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....

cells)}
demipenteractDemipenteract
In five dimensional geometry, a demipenteract or 5-demicube is a semiregular 5-polytope, constructed from a 5-hypercube with alternated vertices deleted.It was discovered by Thorold Gosset...

: 1_{21, 5-ic semiregular figure (16 5-cell and 10 16-cell16-cell
In four dimensional geometry, a 16-cell or hexadecachoron is a regular convex 4-polytope. It is one of the six regular convex 4-polytopes first described by the Swiss mathematician Ludwig Schläfli in the mid-19th century....

facets)}
2 21 polytope: 2_{21, 6-ic semiregular figure (72 5-simplexSimplex
In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...

and 27 5-orthoplex facets)}
3 21 polytope: 3_{21, 7-ic semiregular figure (567 6-simplexSimplex
In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...

and 126 6-orthoplex facets)}
4 21 polytope: 4_{21, 8-ic semiregular figure (17280 7-simplexSimplex
In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...

and 2160 7-orthoplex facets)}
5 21 honeycomb5 21 honeycomb
In geometry, the 521 honeycomb is a uniform tessellation of 8-dimensional Euclidean space.This honeycomb was first studied by Gosset who called it a 9-ic semi-regular figure...

: 5_{21, 9-ic semiregular check tessellates Euclidean 8-space (∞ 8-simplexSimplex
In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...

and ∞ 8-orthoplex facets)}
6 21 honeycomb: 6_{21, tessellates hyperbolic 9-space (∞ 9-simplexSimplex
In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...

and ∞ 9-orthoplex facets)}

Each polytope is constructed from (n − 1)-simplexSimplex
In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...

and (n − 1)-orthoplex facets.

The orthoplex faces are constructed from the Coxeter groupCoxeter group
In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example...

D_n−1 and have a Schlafli symbol of {3^1,n−1,1} rather than the regular {3ⁿ⁻²,4}. This construction is an implication of two "facet types". Half the facets around each orthoplex ridgeRidge (geometry)
In geometry, a ridge is an -dimensional element of an n-dimensional polytope. It is also sometimes called a subfacet for having one lower dimension than a facet.By dimension, this corresponds to:*a vertex of a polygon;...

are attached to another orthoplex, and the others are attached to a simplex. In contrast, every simplex ridge is attached to an orthoplex.

Each has a vertex figureVertex figure
In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...

as the previous form. For example the rectified 5-cell has a vertex figure as a triangular prism.

Elements

Gosset semiregular figures

n-ic
k₂₁
GraphGraph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...

Name
Coxeter-Dynkin
diagramCoxeter-Dynkin diagram
In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors...

FacetsFacet (mathematics)
A facet of a simplicial complex is a maximal simplex.In the general theory of polyhedra and polytopes, two conflicting meanings are currently jostling for acceptability:...

Elements

(n − 1)-simplexSimplex
In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...

{3ⁿ⁻²}
(n − 1)-orthoplex
{3^n−4,1,1}
VerticesVertex (geometry)
In geometry, a vertex is a special kind of point that describes the corners or intersections of geometric shapes.-Of an angle:...

EdgesEdge (geometry)
In geometry, an edge is a one-dimensional line segment joining two adjacent zero-dimensional vertices in a polygon. Thus applied, an edge is a connector for a one-dimensional line segment and two zero-dimensional objects....

FacesFace (geometry)
In geometry, a face of a polyhedron is any of the polygons that make up its boundaries. For example, any of the squares that bound a cube is a face of the cube...

CellsCell (geometry)
In geometry, a cell is a three-dimensional element that is part of a higher-dimensional object.- In polytopes :A cell is a three-dimensional polyhedron element that is part of the boundary of a higher-dimensional polytope, such as a polychoron or honeycomb For example, a cubic honeycomb is made...

4-faces
5-faces
6-faces
7-faces

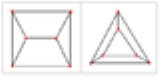
3-ic
−1₂₁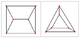

Triangular prismTriangular prism
In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides....

2 triangleTriangle
A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....

s

3 squaresSquare (geometry)
In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles...

6
9
5

4-ic
0₂₁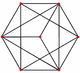

Rectified 5-cellRectified 5-cell
In four dimensional geometry, the rectified 5-cell is a uniform polychoron composed of 5 regular tetrahedral and 5 regular octahedral cells. Each edge has one tetrahedron and two octahedra. Each vertex has two tetrahedra and three octahedra. In total it has 30 triangle faces, 30 edges, and 10...

5 tetrahedronTetrahedron
In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...

5 octahedronOctahedron
In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....

10
30
30
10

5-ic
1₂₁

DemipenteractDemipenteract
In five dimensional geometry, a demipenteract or 5-demicube is a semiregular 5-polytope, constructed from a 5-hypercube with alternated vertices deleted.It was discovered by Thorold Gosset...

16 5-cell

10 16-cell16-cell
In four dimensional geometry, a 16-cell or hexadecachoron is a regular convex 4-polytope. It is one of the six regular convex 4-polytopes first described by the Swiss mathematician Ludwig Schläfli in the mid-19th century....

16
80
160
120
26

6-ic
2₂₁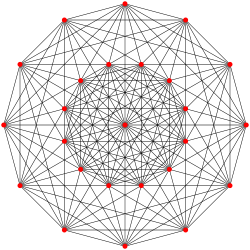

2₂₁ polytope

72 5-simplexes

27 5-orthoplexes

27
216
720
1080
648
99

7-ic
3₂₁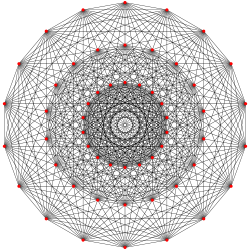

3₂₁ polytope

576 6-simplexes

126 6-orthoplexes

56
756
4032
10080
12096
6048
702

8-ic
4₂₁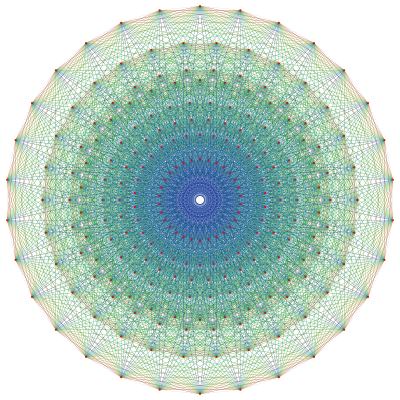

4₂₁ polytope

17280 7-simplexes

2160 7-orthoplexes

240
6720
60480
241920
483840
483840
207360
19440

9-ic

5₂₁

5₂₁ honeycomb5 21 honeycomb
In geometry, the 521 honeycomb is a uniform tessellation of 8-dimensional Euclidean space.This honeycomb was first studied by Gosset who called it a 9-ic semi-regular figure...

∞ 8-simplexes

∞ 8-orthoplexes

∞

10-ic

6₂₁

6₂₁ honeycomb

∞ 9-simplexes

∞ 9-orthoplexes

∞

See also

Uniform 2_k1 polytopeUniform 2 k1 polytope
In geometry, 2k1 polytope is a uniform polytope in n dimensions constructed from the En Coxeter group. The family was named by Coxeter as 2k1 by its bifurcating Coxeter-Dynkin diagram, with a single ring on the end of the 2-node sequence...

family
Uniform 1_k2 polytopeUniform 1 k2 polytope
In geometry, 1k2 polytope is a uniform polytope in n-dimensions constructed from the En Coxeter group. The family was named by Coxeter as 1k2 by its bifurcating Coxeter-Dynkin diagram, with a single ring on the end of the 1-node sequence...

family

External links

PolyGloss v0.05: Gosset figures (Gossetoicosatope)
Regular, SemiRegular, Regular faced and Archimedean polytopes

The source of this article is wikipedia, the free encyclopedia. The text of this article is licensed under the GFDL.}

n-ic	k₂₁	Name Coxeter-Dynkin diagram Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors...	Facets Facet (mathematics) A facet of a simplicial complex is a maximal simplex.In the general theory of polyhedra and polytopes, two conflicting meanings are currently jostling for acceptability:...		Elements
n-ic	k₂₁		(n − 1)-simplex Simplex In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,... {3ⁿ⁻²}	(n − 1)-orthoplex {3^n−4,1,1}	Vertices Vertex (geometry) In geometry, a vertex is a special kind of point that describes the corners or intersections of geometric shapes.-Of an angle:...	Edges Edge (geometry) In geometry, an edge is a one-dimensional line segment joining two adjacent zero-dimensional vertices in a polygon. Thus applied, an edge is a connector for a one-dimensional line segment and two zero-dimensional objects....	Faces Face (geometry) In geometry, a face of a polyhedron is any of the polygons that make up its boundaries. For example, any of the squares that bound a cube is a face of the cube...	Cells Cell (geometry) In geometry, a cell is a three-dimensional element that is part of a higher-dimensional object.- In polytopes :A cell is a three-dimensional polyhedron element that is part of the boundary of a higher-dimensional polytope, such as a polychoron or honeycomb For example, a cubic honeycomb is made...	4-faces	5-faces	6-faces	7-faces
3-ic	−1₂₁	Triangular prism Triangular prism In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides....	2 triangle Triangle A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted .... s	3 squares Square (geometry) In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles...	6	9	5
4-ic	0₂₁	Rectified 5-cell Rectified 5-cell In four dimensional geometry, the rectified 5-cell is a uniform polychoron composed of 5 regular tetrahedral and 5 regular octahedral cells. Each edge has one tetrahedron and two octahedra. Each vertex has two tetrahedra and three octahedra. In total it has 30 triangle faces, 30 edges, and 10...	5 tetrahedron Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...	5 octahedron Octahedron In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....	10	30	30	10
5-ic	1₂₁	Demipenteract Demipenteract In five dimensional geometry, a demipenteract or 5-demicube is a semiregular 5-polytope, constructed from a 5-hypercube with alternated vertices deleted.It was discovered by Thorold Gosset...	16 5-cell	10 16-cell 16-cell In four dimensional geometry, a 16-cell or hexadecachoron is a regular convex 4-polytope. It is one of the six regular convex 4-polytopes first described by the Swiss mathematician Ludwig Schläfli in the mid-19th century....	16	80	160	120	26
6-ic	2₂₁	2₂₁ polytope	72 5-simplexes	27 5-orthoplexes	27	216	720	1080	648	99
7-ic	3₂₁	3₂₁ polytope	576 6-simplexes	126 6-orthoplexes	56	756	4032	10080	12096	6048	702
8-ic	4₂₁	4₂₁ polytope	17280 7-simplexes	2160 7-orthoplexes	240	6720	60480	241920	483840	483840	207360	19440
9-ic	5₂₁	5₂₁ honeycomb 5 21 honeycomb In geometry, the 521 honeycomb is a uniform tessellation of 8-dimensional Euclidean space.This honeycomb was first studied by Gosset who called it a 9-ic semi-regular figure...	∞ 8-simplexes	∞ 8-orthoplexes	∞
10-ic	6₂₁	6₂₁ honeycomb	∞ 9-simplexes	∞ 9-orthoplexes	∞