In geometry

Geometry

Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....

, 2_k1 polytope is a uniform polytope

Uniform polytope

A uniform polytope is a vertex-transitive polytope made from uniform polytope facets of a lower dimension. Uniform polytopes of 2 dimensions are the regular polygons....

 in n dimensions (n = k+4) constructed from the E_n

En (Lie algebra)

In mathematics, especially in Lie theory, En is the Kac–Moody algebra whose Dynkin diagram is a bifurcating graph with three branches of length 1,2, and k, with k=n-4....

 Coxeter group

Coxeter group

In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example...

. The family was named by Coxeter as 2_k1 by its bifurcating Coxeter-Dynkin diagram

Coxeter-Dynkin diagram

In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors...

, with a single ring on the end of the 2-node sequence. It can be named by an expoential Schläfli symbol {3^2,k,1}.

Family members

The family starts uniquely as 6-polytope

6-polytope

In six-dimensional geometry, a uniform polypeton is a six-dimensional uniform polytope. A uniform polypeton is vertex-transitive, and all facets are uniform polytera....

s, but can be extended backwards to include the 5-orthoplex (pentacross

Pentacross

In five-dimensional geometry, a 5-orthoplex, or 5-cross polytope, is a five-dimensional polytope with 10 vertices, 40 edges, 80 triangle faces, 80 tetrahedron cells, 32 5-cell hypercells....

) in 5-dimensions, and the 4-simplex

Simplex

In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...

 (5-cell) in 4-dimensions.

Each polytope is constructed from (n-1)-simplex

Simplex

In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...

 and 2_k-1,1 (n-1)-polytope facets, each has a vertex figure

Vertex figure

In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...

 as an (n-1)-demicube, {3^1,n-2,1}.

The sequence ends with k=6 (n=10), as an infinite hyperbolic tessellation of 9-space.

The complete family of 2_k1 polytope polytopes are:

1. 5-cell: 2₀₁, (5 tetrahedra
   Tetrahedron
   In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...
   
    cells)
2. Pentacross
   Pentacross
   In five-dimensional geometry, a 5-orthoplex, or 5-cross polytope, is a five-dimensional polytope with 10 vertices, 40 edges, 80 triangle faces, 80 tetrahedron cells, 32 5-cell hypercells....
   
   : 2₁₁, (32 5-cell (2₀₁) facets)
3. 2₂₁, (72 5-simplex
   Simplex
   In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...
   
    and 27 5-orthoplex (2₁₁) facets)
4. 2₃₁, (576 6-simplex
   Simplex
   In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...
   
    and 56 2₂₁ facets)
5. 2₄₁, (17280 7-simplex
   Simplex
   In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...
   
    and 240 2₃₁ facets)
6. 2₅₁, tessellates Euclidean 8-space (∞ 8-simplex
   Simplex
   In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...
   
    and ∞ 2₄₁ facets)
7. 2₆₁, tessellates hyperbolic 9-space (∞ 9-simplex
   Simplex
   In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...
   
    and ∞ 2₅₁ facets)

Elements

Gosset 2_k1 figures

n	2k1	Petrie polygon Petrie polygon In geometry, a Petrie polygon for a regular polytope of n dimensions is a skew polygon such that every consecutive sides belong to one of the facets... projection	Name Coxeter-Dynkin diagram Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors...	Facets Facet (mathematics) A facet of a simplicial complex is a maximal simplex.In the general theory of polyhedra and polytopes, two conflicting meanings are currently jostling for acceptability:...		Elements
				2k-1,1 polytope	(n-1)-simplex Simplex In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...	Vertices Vertex (geometry) In geometry, a vertex is a special kind of point that describes the corners or intersections of geometric shapes.-Of an angle:...	Edges Edge (geometry) In geometry, an edge is a one-dimensional line segment joining two adjacent zero-dimensional vertices in a polygon. Thus applied, an edge is a connector for a one-dimensional line segment and two zero-dimensional objects....	Faces Face (geometry) In geometry, a face of a polyhedron is any of the polygons that make up its boundaries. For example, any of the squares that bound a cube is a face of the cube...	Cells Cell (geometry) In geometry, a cell is a three-dimensional element that is part of a higher-dimensional object.- In polytopes :A cell is a three-dimensional polyhedron element that is part of the boundary of a higher-dimensional polytope, such as a polychoron or honeycomb For example, a cubic honeycomb is made...	4-faces	5-faces	6-faces	7-faces
4	201		5-cell {32,0,1}	--	5 {33}	5	10	10	5
5	211		pentacross Pentacross In five-dimensional geometry, a 5-orthoplex, or 5-cross polytope, is a five-dimensional polytope with 10 vertices, 40 edges, 80 triangle faces, 80 tetrahedron cells, 32 5-cell hypercells.... {32,1,1}	16 {32,0,1}	16 {34}	10	40	80	80	32
6	221		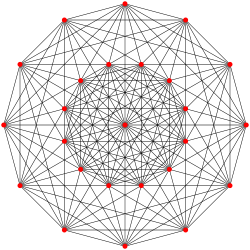2 21 polytope {32,2,1}	27 {32,1,1} Pentacross In five-dimensional geometry, a 5-orthoplex, or 5-cross polytope, is a five-dimensional polytope with 10 vertices, 40 edges, 80 triangle faces, 80 tetrahedron cells, 32 5-cell hypercells....	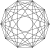72 {35}	27	216	720	1080	648	99
7	231		2 31 polytope {32,3,1}	56 {32,2,1} Gosset 2 21 polytope In 6-dimensional geometry, the 221 polytope is a uniform 6-polytope, constructed within the symmetry of the E6 group. It was discovered by Thorold Gosset, published in his 1900 paper. He called it an 6-ic semi-regular figure....	576 {36}	126	2016	10080	20160	16128	4788	632
8	241		2 41 polytope {32,4,1}	240 {32,3,1} Gosset 2 31 polytope In 7-dimensional geometry, 231 is a uniform polytope, constructed from the E7 group.Coxeter named it 231 by its bifurcating Coxeter-Dynkin diagram, with a single ring on the end of one of the 2-node sequences....	17280 {37}	2160	69120	483840	1209600	1209600	544320	144960	17520
9	251		2 51 honeycomb (8-space tessellation) {32,5,1}	∞ {32,4,1} Gosset 2 41 polytope In 8-dimensional geometry, the 241 is a uniform 8-polytope, constructed within the symmetry of the E8 group.Coxeter named it 241 by its bifurcating Coxeter-Dynkin diagram, with a single ring on the end of the 2-node sequences....	∞ {38}	∞
10	261		2 61 honeycomb (9-space tessellation) {32,6,1}	∞ {32,5,1}	∞ {39}	∞

See also

• k₂₁ polytope family
• 1_k2 polytope
  Uniform 1 k2 polytope
  In geometry, 1k2 polytope is a uniform polytope in n-dimensions constructed from the En Coxeter group. The family was named by Coxeter as 1k2 by its bifurcating Coxeter-Dynkin diagram, with a single ring on the end of the 1-node sequence...
  
  family

External links

• PolyGloss v0.05: Gosset figures (Gossetoctotope)