
Pentacross
Encyclopedia
| Regular 5-orthoplex (pentacross) |
|
|---|---|
Orthogonal projection inside Petrie polygon Petrie polygon In geometry, a Petrie polygon for a regular polytope of n dimensions is a skew polygon such that every consecutive sides belong to one of the facets... |
|
| Type | Regular 5-polytope 5-polytope In five-dimensional geometry, a 5-polytope is a 5-dimensional polytope, bounded by facets. Each polyhedral cell being shared by exactly two polychoron facets. A proposed name for 5-polytopes is polyteron.-Definition:... |
| Family | orthoplex |
| Schläfli symbol | {3,3,3,4} {3,3,31,1} |
| Coxeter-Dynkin diagram Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... s |
|
| Hypercells | 32 {33} |
| Cells | 80 {3,3} Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids... |
| Faces | 80 {3} Triangle A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted .... |
| Edges | 40 |
| Vertices | 10 |
| Vertex figure Vertex figure In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:... |
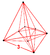 16-cell 16-cell In four dimensional geometry, a 16-cell or hexadecachoron is a regular convex 4-polytope. It is one of the six regular convex 4-polytopes first described by the Swiss mathematician Ludwig Schläfli in the mid-19th century.... |
| Petrie polygon Petrie polygon In geometry, a Petrie polygon for a regular polytope of n dimensions is a skew polygon such that every consecutive sides belong to one of the facets... |
decagon Decagon In geometry, a decagon is any polygon with ten sides and ten angles, and usually refers to a regular decagon, having all sides of equal length and each internal angle equal to 144°... |
| Coxeter group Coxeter group In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example... s |
BC5, [3,3,3,4] D5, [32,1,1] |
| Dual | 5-cube |
| Properties | convex Convex polytope A convex polytope is a special case of a polytope, having the additional property that it is also a convex set of points in the n-dimensional space Rn... |
In five-dimensional geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, a 5-orthoplex, or 5-cross polytope, is a five-dimensional polytope with 10 vertices
Vertex (geometry)
In geometry, a vertex is a special kind of point that describes the corners or intersections of geometric shapes.-Of an angle:...
, 40 edge
Edge (geometry)
In geometry, an edge is a one-dimensional line segment joining two adjacent zero-dimensional vertices in a polygon. Thus applied, an edge is a connector for a one-dimensional line segment and two zero-dimensional objects....
s, 80 triangle faces
Face (geometry)
In geometry, a face of a polyhedron is any of the polygons that make up its boundaries. For example, any of the squares that bound a cube is a face of the cube...
, 80 tetrahedron cells, 32 5-cell hypercell
Hypercell
In geometry, a hypercell is a descriptive term for an element of a polytope or tessellation, usually representing an element one dimension higher than a cell. The most generally accepted term is 4-face because it contains a 4-dimensional interior...
s.
It has two constructed forms, the first being regular with Schläfli symbol {33,4}, and the second with alternately labeled (checkerboarded) facets, with Schläfli symbol {32,1,1} or Coxeter symbol 211.
Alternate names
- pentacross, derived from combining the family name cross polytope with pente for five (dimensions) in GreekGreek languageGreek is an independent branch of the Indo-European family of languages. Native to the southern Balkans, it has the longest documented history of any Indo-European language, spanning 34 centuries of written records. Its writing system has been the Greek alphabet for the majority of its history;...
. - Triacontakaiditeron - as a 32-facetted 5-polytope5-polytopeIn five-dimensional geometry, a 5-polytope is a 5-dimensional polytope, bounded by facets. Each polyhedral cell being shared by exactly two polychoron facets. A proposed name for 5-polytopes is polyteron.-Definition:...
(polyteron).
Related polytopes
It is a part of an infinite family of polytopes, called cross-polytopeCross-polytope
In geometry, a cross-polytope, orthoplex, hyperoctahedron, or cocube is a regular, convex polytope that exists in any number of dimensions. The vertices of a cross-polytope are all the permutations of . The cross-polytope is the convex hull of its vertices...
s or orthoplexes. The dual polytope is the 5-hypercube
Hypercube
In geometry, a hypercube is an n-dimensional analogue of a square and a cube . It is a closed, compact, convex figure whose 1-skeleton consists of groups of opposite parallel line segments aligned in each of the space's dimensions, perpendicular to each other and of the same length.An...
or 5-cube.
Construction
There are two Coxeter groupCoxeter group
In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example...
s associated with the 5-orthoplex, one regular
Regular polytope
In mathematics, a regular polytope is a polytope whose symmetry is transitive on its flags, thus giving it the highest degree of symmetry. All its elements or j-faces — cells, faces and so on — are also transitive on the symmetries of the polytope, and are regular polytopes of...
, dual of the penteract
Penteract
In five dimensional geometry, a 5-cube is a name for a five dimensional hypercube with 32 vertices, 80 edges, 80 square faces, 40 cubic cells, and 10 tesseract hypercells....
with the C5 or [4,3,3,3] Coxeter group
Coxeter group
In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example...
, and a lower symmetry with two copies of 5-cell facets, alternating, with the D5 or [32,1,1] Coxeter group.
Cartesian coordinates
Cartesian coordinates for the vertices of a 5-orthoplex, centered at the origin are- (±1,0,0,0,0), (0,±1,0,0,0), (0,0,±1,0,0), (0,0,0,±1,0), (0,0,0,0,±1)
Other images
 Precisely, the perspective projection 3D to 2D of stereographic projection Stereographic projection The stereographic projection, in geometry, is a particular mapping that projects a sphere onto a plane. The projection is defined on the entire sphere, except at one point — the projection point. Where it is defined, the mapping is smooth and bijective. It is conformal, meaning that it... 4D to 3D of Schlegel diagram 5D to 4D of the 5-orthoplex. 10 sets of 4 edges forms 10 circles in the 4D Schlegel diagram: two of these circles are straight lines because contains the center of projection. |

