Hypercube
Encyclopedia
 |
 |
| Cube Cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and... (3-cube) |
Tesseract Tesseract In geometry, the tesseract, also called an 8-cell or regular octachoron or cubic prism, is the four-dimensional analog of the cube. The tesseract is to the cube as the cube is to the square. Just as the surface of the cube consists of 6 square faces, the hypersurface of the tesseract consists of 8... (4-cube) |
|---|
In geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, a hypercube is an n-dimensional analogue of a square
Square (geometry)
In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles...
(n = 2) and a cube
Cube
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and...
(n = 3). It is a closed
Closed set
In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
, compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
, convex
Convex polytope
A convex polytope is a special case of a polytope, having the additional property that it is also a convex set of points in the n-dimensional space Rn...
figure whose 1-skeleton consists of groups of opposite parallel
Parallel (geometry)
Parallelism is a term in geometry and in everyday life that refers to a property in Euclidean space of two or more lines or planes, or a combination of these. The assumed existence and properties of parallel lines are the basis of Euclid's parallel postulate. Two lines in a plane that do not...
line segment
Line segment
In geometry, a line segment is a part of a line that is bounded by two end points, and contains every point on the line between its end points. Examples of line segments include the sides of a triangle or square. More generally, when the end points are both vertices of a polygon, the line segment...
s aligned in each of the space's dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
s, perpendicular
Perpendicular
In geometry, two lines or planes are considered perpendicular to each other if they form congruent adjacent angles . The term may be used as a noun or adjective...
to each other and of the same length.
An n-dimensional hypercube is also called an n-cube. The term "measure polytope" is also used, notably in the work of H.S.M. Coxeter (originally from Elte, 1912), but it has now been superseded.
The hypercube is the special case of a hyperrectangle
Hyperrectangle
In geometry, an orthotope is the generalization of a rectangle for higher dimensions, formally defined as the Cartesian product of intervals....
(also called an orthotope).
A unit hypercube is a hypercube whose side has length one unit. Often, the hypercube whose corners (or vertices) are the 2n points in Rn with coordinates equal to 0 or 1 is called "the" unit hypercube.
Construction
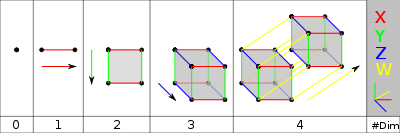
- 0 – A point is a hypercube of dimension zero.
- 1 – If one moves this point one unit length, it will sweep out a line segment, which is a unit hypercube of dimension one.
- 2 – If one moves this line segment its length in a perpendicularPerpendicularIn geometry, two lines or planes are considered perpendicular to each other if they form congruent adjacent angles . The term may be used as a noun or adjective...
direction from itself; it sweeps out a 2-dimensional square. - 3 – If one moves the square one unit length in the direction perpendicular to the plane it lies on, it will generate a 3-dimensional cube.
- 4 – If one moves the cube one unit length into the fourth dimension, it generates a 4-dimensional unit hypercube (a unit tesseractTesseractIn geometry, the tesseract, also called an 8-cell or regular octachoron or cubic prism, is the four-dimensional analog of the cube. The tesseract is to the cube as the cube is to the square. Just as the surface of the cube consists of 6 square faces, the hypersurface of the tesseract consists of 8...
).
This can be generalized to any number of dimensions. This process of sweeping out volumes can be formalized mathematically as a Minkowski sum: the d-dimensional hypercube is the Minkowski sum of d mutually perpendicular unit-length line segments, and is therefore an example of a zonotope.
The 1-skeleton of a hypercube is a hypercube graph.
Coordinates
A unit hypercube of n dimensions is the convex hullConvex hull
In mathematics, the convex hull or convex envelope for a set of points X in a real vector space V is the minimal convex set containing X....
of the points given by all sign permutations of the Cartesian coordinates
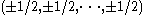. It has an edge length of 1 and an n-dimensional volume of 1.An n-dimensional hypercube is also often regarded as the convex hull of all sign permutations of the coordinates
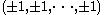. This form is often chosen due to ease of writing out the coordinates. Its edge length is 2, and its n-dimensional volume is 2n.Related families of polytopes
The hypercubes are one of the few families of regular polytopeRegular polytope
In mathematics, a regular polytope is a polytope whose symmetry is transitive on its flags, thus giving it the highest degree of symmetry. All its elements or j-faces — cells, faces and so on — are also transitive on the symmetries of the polytope, and are regular polytopes of...
s that are represented in any number of dimensions.
The hypercube (offset) family is one of three regular polytope
Regular polytope
In mathematics, a regular polytope is a polytope whose symmetry is transitive on its flags, thus giving it the highest degree of symmetry. All its elements or j-faces — cells, faces and so on — are also transitive on the symmetries of the polytope, and are regular polytopes of...
families, labeled by Coxeter as γn. The other two are the hypercube dual family, the cross-polytope
Cross-polytope
In geometry, a cross-polytope, orthoplex, hyperoctahedron, or cocube is a regular, convex polytope that exists in any number of dimensions. The vertices of a cross-polytope are all the permutations of . The cross-polytope is the convex hull of its vertices...
s, labeled as βn, and the simplices
Simplex
In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...
, labeled as αn. A fourth family, the infinite tessellations of hypercubes, he labeled as δn.
Another related family of semiregular and uniform polytope
Uniform polytope
A uniform polytope is a vertex-transitive polytope made from uniform polytope facets of a lower dimension. Uniform polytopes of 2 dimensions are the regular polygons....
s is the demihypercubes, which are constructed from hypercubes with alternate vertices deleted and simplex
Simplex
In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...
facets added in the gaps, labeled as hγn.
Elements
A hypercube of dimension n has 2n "sides" (a 1-dimensional line has 2 end points; a 2-dimensional square has 4 sides or edges; a 3-dimensional cube has 6 2-dimensional faces; a 4-dimensional tesseract has 8 cellCell (geometry)
In geometry, a cell is a three-dimensional element that is part of a higher-dimensional object.- In polytopes :A cell is a three-dimensional polyhedron element that is part of the boundary of a higher-dimensional polytope, such as a polychoron or honeycomb For example, a cubic honeycomb is made...
s). The number of vertices (points) of a hypercube is 2n (a cube has 23 vertices, for instance).
A simple formula to calculate the number of "n-2"-faces in an n-dimensional hypercube is:
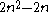
The number of m-dimensional hypercubes (just referred to as m-cube from here on) on the boundary of an n-cube is
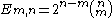, where 
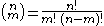and n! denotes the factorialFactorial
In mathematics, the factorial of a non-negative integer n, denoted by n!, is the product of all positive integers less than or equal to n...
of n.
For example, the boundary of a 4-cube (n=4) contains 8 cubes (3-cubes), 24 squares (2-cubes), 32 lines (1-cubes) and 16 vertices (0-cubes).
This identity can be proved by combinatorial arguments; each of the
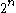vertices defines a vertex ina
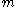-dimensional boundary. There are 
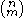ways of choosing which lines ("sides") that defines the subspace that the boundary is in. But, each side is counted 
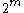times since it has that many vertices, we need to divide with this number. Hence the identity above.These numbers can also be generated by the linear recurrence relation
Recurrence relation
In mathematics, a recurrence relation is an equation that recursively defines a sequence, once one or more initial terms are given: each further term of the sequence is defined as a function of the preceding terms....
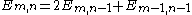, with 
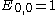, and undefined elements = 0.For example, extending a square via its 4 vertices adds one extra line (edge) per vertex, and also adds the final second square, to form a cube, giving
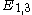= 12 lines in total.| m | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| n Polytope In elementary geometry, a polytope is a geometric object with flat sides, which exists in any general number of dimensions. A polygon is a polytope in two dimensions, a polyhedron in three dimensions, and so on in higher dimensions... |
γn | n-cube | Names Schläfli symbol Coxeter-Dynkin Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... |
Vertices Vertex (geometry) In geometry, a vertex is a special kind of point that describes the corners or intersections of geometric shapes.-Of an angle:... |
Edges Edge (geometry) In geometry, an edge is a one-dimensional line segment joining two adjacent zero-dimensional vertices in a polygon. Thus applied, an edge is a connector for a one-dimensional line segment and two zero-dimensional objects.... |
Faces Face (geometry) In geometry, a face of a polyhedron is any of the polygons that make up its boundaries. For example, any of the squares that bound a cube is a face of the cube... |
Cells Cell (geometry) In geometry, a cell is a three-dimensional element that is part of a higher-dimensional object.- In polytopes :A cell is a three-dimensional polyhedron element that is part of the boundary of a higher-dimensional polytope, such as a polychoron or honeycomb For example, a cubic honeycomb is made... (3-faces) |
4-faces (Hypercells) | 5-faces | 6-faces | 7-faces | 8-faces | 9-faces | 10-faces |
| 0 | γ0 | 0-cube | Point - |
1 | ||||||||||
| 1 | γ1 | 1-cube | Line segment Line segment In geometry, a line segment is a part of a line that is bounded by two end points, and contains every point on the line between its end points. Examples of line segments include the sides of a triangle or square. More generally, when the end points are both vertices of a polygon, the line segment... {} |
2 | 1 | |||||||||
| 2 | γ2 | 2-cube | Square Square (geometry) In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles... Tetragon {4} |
4 | 4 | 1 | ||||||||
| 3 | γ3 | 3-cube | Cube Cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and... Hexahedron {4,3} |
8 | 12 | 6 | 1 | |||||||
| 4 | γ4 | 4-cube | Tesseract Tesseract In geometry, the tesseract, also called an 8-cell or regular octachoron or cubic prism, is the four-dimensional analog of the cube. The tesseract is to the cube as the cube is to the square. Just as the surface of the cube consists of 6 square faces, the hypersurface of the tesseract consists of 8... Octachoron {4,3,3} |
16 | 32 | 24 | 8 | 1 | ||||||
| 5 5-polytope In five-dimensional geometry, a 5-polytope is a 5-dimensional polytope, bounded by facets. Each polyhedral cell being shared by exactly two polychoron facets. A proposed name for 5-polytopes is polyteron.-Definition:... |
γ5 | 5-cube | Penteract Penteract In five dimensional geometry, a 5-cube is a name for a five dimensional hypercube with 32 vertices, 80 edges, 80 square faces, 40 cubic cells, and 10 tesseract hypercells.... Decateron {4,3,3,3} |
32 | 80 | 80 | 40 | 10 | 1 | |||||
| 6 6-polytope In six-dimensional geometry, a uniform polypeton is a six-dimensional uniform polytope. A uniform polypeton is vertex-transitive, and all facets are uniform polytera.... |
γ6 | 6-cube | Hexeract Hexeract In geometry, a 6-cube is a six-dimensional hypercube with 64 vertices, 192 edges, 240 square faces, 160 cubic cells, 60 tesseract 4-faces, and 12 5-cube 5-faces.... Dodecapeton {4,3,3,3,3} |
64 | 192 | 240 | 160 | 60 | 12 | 1 | ||||
| 7 7-polytope In seven-dimensional geometry, a 7-polytope is a polytope contained by 6-polytope facets. Each 5-polytope ridge being shared by exactly two 6-polytope facets.... |
γ7 | 7-cube | Hepteract Hepteract In geometry, a 7-cube is a seven-dimensional hypercube with 128 vertices, 448 edges, 672 square faces, 560 cubic cells, 280 tesseract 4-faces, 84 penteract 5-faces, and 14 hexeract 6-faces.... Tetradeca-7-tope {4,3,3,3,3,3} |
128 | 448 | 672 | 560 | 280 | 84 | 14 | 1 | |||
| 8 8-polytope In eight-dimensional geometry, a polyzetton is a polytope contained by 7-polytope facets. Each 6-polytope ridge being shared by exactly two 7-polytope facets.... |
γ8 | 8-cube | Octeract Octeract In geometry, an 8-cube is an eight-dimensional hypercube . It has 256 vertices, 1024 edges, 1792 square faces, 1792 cubic cells, 1120 tesseract 4-faces, 448 5-cube 5-faces, 112 6-cube 6-faces, and 16 7-cube 7-faces.... Hexadeca-8-tope {4,3,3,3,3,3,3} |
256 | 1024 | 1792 | 1792 | 1120 | 448 | 112 | 16 | 1 | ||
| 9 9-polytope In nine-dimensional geometry, a polyyotton is a polytope contained by 8-polytope facets. Each 7-polytope ridge being shared by exactly two 8-polytope facets.... |
γ9 | 9-cube | Enneract Enneract In geometry, a 9-cube is a nine-dimensional hypercube with 512 vertices, 2304 edges, 4608 square faces, 5376 cubic cells, 4032 tesseract 4-faces, 2016 5-cube 5-faces, 672 6-cube 6-faces, 144 7-cube 7-faces, and 18 8-cube 8-faces.... Octadeca-9-tope {4,3,3,3,3,3,3,3} |
512 | 2304 | 4608 | 5376 | 4032 | 2016 | 672 | 144 | 18 | 1 | |
| 10 10-polytope In ten-dimensional geometry, a 10-polytope is a 10 dimensional polytope contained by 9-polytope facets. Each 8-polytope ridge being shared by exactly two 9-polytope facets.... |
γ10 | 10-cube | Dekeract 10-cube In geometry, a 10-cube is a ten-dimensional hypercube. It has 1024 vertices, 5120 edges, 11520 square faces, 15360 cubic cells, 13440 tesseract 4-faces, 8064 5-cube 5-faces, 3360 6-cube 6-faces, 960 7-cube 7-faces, 180 8-cube 8-faces, and 20 9-cube 9-faces.... icosa-10-tope {4,3,3,3,3,3,3,3,3} |
1024 | 5120 | 11520 | 15360 | 13440 | 8064 | 3360 | 960 | 180 | 20 | 1 |
Graphs
An n-cube can be projected inside a regular 2n-gonal polygon by a skew orthogonal projection, shown here from the line segment to the dodekeract.Line segment |
Square |
Cube |
4-cube (tesseract) |
5-cube (penteract) |
6-cube (hexeract) |
7-cube (hepteract) |
8-cube (octeract) |
9-cube (enneract) |
10-cube (dekeract) |
11-cube (hendekeract) |
12-cube (dodekeract) |
Relation to n-simplices
The graph of the n-hypercube's edges is isomorphicIsomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
to the Hasse diagram
Hasse diagram
In order theory, a branch of mathematics, a Hasse diagram is a type of mathematical diagram used to represent a finite partially ordered set, in the form of a drawing of its transitive reduction...
of the (n-1)-simplex
Simplex
In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...
's face lattice. This can be seen by orienting the n-hypercube so that two opposite vertices lie vertically, corresponding to the (n-1)-simplex itself and the null polytope, respectively. Each vertex connected to the top vertex then uniquely maps to one of the (n-1)-simplex's facets (n-2 faces), and each vertex connected to those vertices maps to one of the simplex's n-3 faces, and so forth, and the vertices connected to the bottom vertex map to the simplex's vertices.
This relation may be used to generate the face lattice of an (n-1)-simplex efficiently, since face lattice enumeration algorithms applicable to general polytopes are more computationally expensive.
See also
- Hyperoctahedral groupHyperoctahedral groupIn mathematics, a hyperoctahedral group is an important type of group that can be realized as the group of symmetries of a hypercube or of a cross-polytope. Groups of this type are identified by a parameter n, the dimension of the hypercube....
, the symmetry group of the hypercube - HypersphereHypersphereIn mathematics, an n-sphere is a generalization of the surface of an ordinary sphere to arbitrary dimension. For any natural number n, an n-sphere of radius r is defined as the set of points in -dimensional Euclidean space which are at distance r from a central point, where the radius r may be any...
- SimplexSimplexIn geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...
- Hypercube interconnection network of computer architecture
External links
- www.4d-screen.de (Rotation of 4D – 7D-Cube)
- Rotating a Hypercube by Enrique Zeleny, Wolfram Demonstrations ProjectWolfram Demonstrations ProjectThe Wolfram Demonstrations Project is hosted by Wolfram Research, whose stated goal is to bring computational exploration to the widest possible audience. It consists of an organized, open-source collection of small interactive programs called Demonstrations, which are meant to visually and...
. - Stereoscopic Animated Hypercube