
6-polytope
Encyclopedia
6-simplex |
Truncated 6-simplex Truncated 6-simplex In six-dimensional geometry, a truncated 6-simplex is a convex uniform 6-polytope, being a truncation of the regular 6-simplex.There are unique 3 degrees of truncation. Vertices of the truncation 6-simplex are located as pairs on the edge of the 6-simplex. Vertices of the bitruncated 6-simplex are... |
Rectified 6-simplex Rectified 6-simplex In six-dimensional geometry, a rectified 6-simplex is a convex uniform 6-polytope, being a rectification of the regular 6-simplex.There are three unique degrees of rectifications, including the zeroth, the 6-simplex itself. Vertices of the rectified 6-simplex are located at the edge-centers of the... |
|||||||||
Cantellated 6-simplex Cantellated 6-simplex In six-dimensional geometry, a cantellated 6-simplex is a convex uniform 6-polytope, being a cantellation of the regular 6-simplex.There are unique 4 degrees of cantellation for the 6-simplex, including truncations.- Cantellated 6-simplex:... |
Runcinated 6-simplex Runcinated 6-simplex In six-dimensional geometry, a runcinated 6-simplex is a convex uniform 6-polytope constructed as a runcination of the regular 6-simplex.... |
||||||||||
Stericated 6-simplex Stericated 6-simplex In six-dimensional geometry, a stericated 6-simplex is a convex uniform 6-polytope with 4th order truncations of the regular 6-simplex.... |
Pentellated 6-simplex Pentellated 6-simplex In six-dimensional geometry, a pentellated 6-simplex is a convex uniform 6-polytope with 5th order truncations of the regular 6-simplex.There are unique 10 degrees of pentellations of the 6-simplex with permutations of truncations, cantellations, runcinations, and sterications... |
||||||||||
6-orthoplex |
Truncated 6-orthoplex Truncated 6-orthoplex In six-dimensional geometry, a truncated 6-orthoplex is a convex uniform 6-polytope, being a truncation of the regular 6-orthoplex.There are 5 degrees of truncation for the 6-orthoplex. Vertices of the truncated 6-orthoplex are located as pairs on the edge of the 6-orthoplex. Vertices of the... |
Rectified 6-orthoplex |
|||||||||
Cantellated 6-orthoplex Cantellated 6-orthoplex In six-dimensional geometry, a cantellated 6-orthoplex is a convex uniform 6-polytope, being a cantellation of the regular 6-orthoplex.There are 8 cantellation for the 6-orthoplex including truncations... |
Runcinated 6-orthoplex Runcinated 6-orthoplex In six-dimensional geometry, a runcinated 6-orthplex is a convex uniform 6-polytope with 3rd order truncations of the regular 6-orthoplex.There are 12 unique runcinations of the 6-orthoplex with permutations of truncations, and cantellations... |
Stericated 6-orthoplex Stericated 6-orthoplex In six-dimensional geometry, a stericated 6-orthoplex is a convex uniform 6-polytope, constructed as a sterication of the regular 6-orthoplex.... |
|||||||||
Cantellated 6-cube Cantellated 6-cube In six-dimensional geometry, a cantellated 6-cube is a convex uniform 6-polytope, being a cantellation of the regular 6-cube.There are 8 cantellations for the 6-cube, including truncations... |
Runcinated 6-cube Runcinated 6-cube In six-dimensional geometry, a runcinated 6-cube is a convex uniform 6-polytope with 3rd order truncations of the regular 6-cube.There are 12 unique runcinations of the 6-cube with permutations of truncations, and cantellations... |
||||||||||
Stericated 6-cube Stericated 6-cube In six-dimensional geometry, a stericated 6-cube is a convex uniform 6-polytope, constructed as a sterication of the regular 6-cube.... |
Pentellated 6-cube Pentellated 6-cube In six-dimensional geometry, a pentellated 6-cube is a convex uniform 6-polytope with 5th order truncations of the regular 6-cube.There are unique 16 degrees of pentellations of the 6-cube with permutations of truncations, cantellations, runcinations, and sterications... |
||||||||||
6-cube |
Truncated 6-cube |
Rectified 6-cube Rectified 6-cube In six-dimensional geometry, a rectified 6-cube is a convex uniform 6-polytope, being a rectification of the regular 6-cube.There are unique 6 degrees of rectifications, the zeroth being the 6-cube, and the 6th and last being the 6-orthoplex. Vertices of the rectified 6-cube are located at the... |
|||||||||
6-demicube |
Truncated 6-demicube |
Cantellated 6-demicube Cantellated 6-demicube In six-dimensional geometry, a cantellated 6-demicube is a convex uniform 6-polytope, being a cantellation of the uniform 6-demicube. There are 2 unique cantellation for the 6-demicube including a truncation.- Cantellated 6-demicube:... |
|||||||||
Runcinated 6-demicube Runcinated 6-demicube In six-dimensional geometry, a runcinated 6-demicube is a convex uniform 6-polytope with 3rd order truncations of the uniform 6-demicube.There are unique 4 runcinations of the 6-demicube, including permutations of truncations, and cantellations.... |
Stericated 6-demicube Stericated 6-demicube In six-dimensional geometry, a stericated 6-demicube is a convex uniform 6-polytope, constructed as a sterication of the 6-demicube.... |
||||||||||
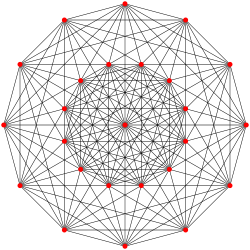 221 |
122 |
||||||||||
Truncated 221 |
Truncated 122 |
||||||||||
In six-dimensional geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, a uniform polypeton (or uniform 6-polytope
6-polytope
In six-dimensional geometry, a uniform polypeton is a six-dimensional uniform polytope. A uniform polypeton is vertex-transitive, and all facets are uniform polytera....
) is a six-dimensional uniform polytope
Uniform polytope
A uniform polytope is a vertex-transitive polytope made from uniform polytope facets of a lower dimension. Uniform polytopes of 2 dimensions are the regular polygons....
. A uniform polypeton is vertex-transitive
Vertex-transitive
In geometry, a polytope is isogonal or vertex-transitive if, loosely speaking, all its vertices are the same...
, and all facets are uniform polytera
Uniform polyteron
In geometry, a uniform polyteron is a five-dimensional uniform polytope. By definition, a uniform polyteron is vertex-transitive and constructed from uniform polychoron facets....
.
The complete set of convex uniform polypeta has not been determined, but most can be made as Wythoff construction
Wythoff construction
In geometry, a Wythoff construction, named after mathematician Willem Abraham Wythoff, is a method for constructing a uniform polyhedron or plane tiling. It is often referred to as Wythoff's kaleidoscopic construction.- Construction process :...
s from a small set of symmetry groups. These construction operations are represented by the permutations of rings of the Coxeter-Dynkin diagram
Coxeter-Dynkin diagram
In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors...
s. Each combination of at least one ring on every connected group of nodes in the diagram produces a uniform 6-polytope.
The simplest uniform polypeta are regular polytope
Regular polytope
In mathematics, a regular polytope is a polytope whose symmetry is transitive on its flags, thus giving it the highest degree of symmetry. All its elements or j-faces — cells, faces and so on — are also transitive on the symmetries of the polytope, and are regular polytopes of...
s: the 6-simplex {3,3,3,3,3}, the 6-cube (hexeract) {4,3,3,3,3}, and the 6-orthoplex (hexacross) {3,3,3,3,4}.
Uniform 6-polytopes by fundamental Coxeter groups
Uniform 6-polytopes with reflective symmetry can be generated by these four Coxeter groups, represented by permutations of rings of the Coxeter-Dynkin diagramCoxeter-Dynkin diagram
In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors...
s.
There are four fundamental reflective symmety groups which generate 153 unique uniform 6-polytopes.
| # | Coxeter group Coxeter group In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example... |
Coxeter-Dynkin diagram Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... |
|
|---|---|---|---|
| 1 | A6 | [35] | |
| 2 | B6 | [4,34] | |
| 3a | D6 | [33,1,1] | |
| 4 | E6 | [32,2,1] | |
Uniform prismatic families
Uniform prismThere are 6 categorical uniform
Uniform polytope
A uniform polytope is a vertex-transitive polytope made from uniform polytope facets of a lower dimension. Uniform polytopes of 2 dimensions are the regular polygons....
prisms based the uniform 5-polytopes.
| # | Coxeter group Coxeter group In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example... |
Coxeter-Dynkin diagram Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... |
Notes | |
|---|---|---|---|---|
| 1 | A5×A1 | [3,3,3,3] × [ ] | Prism family based on 6-simplex | |
| 2 | B5×A1 | [4,3,3,3] × [ ] | Prism family based on 6-cube | |
| 3a | D5×A1 | [32,1,1] × [ ] | Prism family based on 6-demicube | |
| # | Coxeter group Coxeter group In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example... |
Coxeter-Dynkin diagram Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... |
Notes | |
|---|---|---|---|---|
| 4 | A3×I2(p)×A1 | [3,3] × [p] × [ ] | Prism family based on tetrahedral Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids... -p-gonal duoprism Duoprism In geometry of 4 dimensions or higher, a duoprism is a polytope resulting from the Cartesian product of two polytopes, each of two dimensions or higher... s |
|
| 5 | B3×I2(p)×A1 | [4,3] × [p] × [ ] | Prism family based on cubic Cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and... -p-gonal duoprism Duoprism In geometry of 4 dimensions or higher, a duoprism is a polytope resulting from the Cartesian product of two polytopes, each of two dimensions or higher... s |
|
| 6 | H3×I2(p)×A1 | [5,3] × [p] × [ ] | Prism family based on dodecahedral-p-gonal duoprism Duoprism In geometry of 4 dimensions or higher, a duoprism is a polytope resulting from the Cartesian product of two polytopes, each of two dimensions or higher... s |
|
Uniform duoprism
There are 11 categorical uniform
Uniform polytope
A uniform polytope is a vertex-transitive polytope made from uniform polytope facets of a lower dimension. Uniform polytopes of 2 dimensions are the regular polygons....
duoprism
Duoprism
In geometry of 4 dimensions or higher, a duoprism is a polytope resulting from the Cartesian product of two polytopes, each of two dimensions or higher...
atic families of polytopes based on Cartesian product
Cartesian product
In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
s of lower dimensional uniform polytopes. Five are formed as the product of a uniform polychoron
Uniform polychoron
In geometry, a uniform polychoron is a polychoron or 4-polytope which is vertex-transitive and whose cells are uniform polyhedra....
with a regular polygon
Regular polygon
A regular polygon is a polygon that is equiangular and equilateral . Regular polygons may be convex or star.-General properties:...
, and six are formed by the product of two uniform polyhedra
Uniform polyhedron
A uniform polyhedron is a polyhedron which has regular polygons as faces and is vertex-transitive...
:
| # | Coxeter group Coxeter group In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example... |
Coxeter-Dynkin diagram Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... |
Notes | |
|---|---|---|---|---|
| 1 | A4×I2(p) | [3,3,3] × [p] | Family based on 5-cell-p-gonal duoprisms. | |
| 2 | B4×I2(p) | [4,3,3] × [p] | Family based on tesseract Tesseract In geometry, the tesseract, also called an 8-cell or regular octachoron or cubic prism, is the four-dimensional analog of the cube. The tesseract is to the cube as the cube is to the square. Just as the surface of the cube consists of 6 square faces, the hypersurface of the tesseract consists of 8... -p-gonal duoprisms. |
|
| 3 | F4×I2(p) | [3,4,3] × [p] | Family based on 24-cell-p-gonal duoprisms. | |
| 4 | H4×I2(p) | [5,3,3] × [p] | Family based on 120-cell-p-gonal duoprisms. | |
| 5 | D4×I2(p) | [31,1,1] × [p] | Family based on demitesseract-p-gonal duoprisms. | |
| # | Coxeter group Coxeter group In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example... |
Coxeter-Dynkin diagram Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... |
Notes | |
|---|---|---|---|---|
| 6 | A32 | [3,3]2 | Family based on tetrahedral Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids... duoprisms. |
|
| 7 | A3×B3 | [3,3] × [4,3] | Family based on tetrahedral Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids... -cubic Cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and... duoprisms. |
|
| 8 | A3×H3 | [3,3] × [5,3] | Family based on tetrahedral Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids... -dodecahedral duoprisms. |
|
| 9 | B32 | [4,3]2 | Family based on cubic Cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and... duoprisms. |
|
| 10 | B3×H3 | [4,3] × [5,3] | Family based on cubic Cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and... -dodecahedral duoprisms. |
|
| 11 | H32 | [5,3]2 | Family based on dodecahedral duoprisms. | |
Uniform triaprism
There is one infinite family of uniform
Uniform polytope
A uniform polytope is a vertex-transitive polytope made from uniform polytope facets of a lower dimension. Uniform polytopes of 2 dimensions are the regular polygons....
triaprism
Triaprism
In geometry of 6 dimensions or higher, a triaprism is a polytope resulting from the Cartesian product of three polytopes, each of two dimensions or higher...
atic families of polytopes constructed as a Cartesian product
Cartesian product
In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
s of three regular polygons. Each combination of at least one ring on every connected group produces a uniform prismatic 6-polytope.
| # | Coxeter group Coxeter group In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example... |
Coxeter-Dynkin diagram Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... |
Notes | |
|---|---|---|---|---|
| 1 | I2(p)×I2(q)×I2(r) | [p] × [q] × [r] | Family based on p,q,r-gonal triprisms | |
Enumerating the convex uniform 6-polytopes
- SimplexSimplexIn geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...
family: A6 [34] -- 35 uniform 6-polytopes as permutations of rings in the group diagram, including one regular:
- {34} - 6-simplex -
- 35 uniform 6-polytopes as permutations of rings in the group diagram, including one regular:
- HypercubeHypercubeIn geometry, a hypercube is an n-dimensional analogue of a square and a cube . It is a closed, compact, convex figure whose 1-skeleton consists of groups of opposite parallel line segments aligned in each of the space's dimensions, perpendicular to each other and of the same length.An...
/orthoplex family: B6 [4,34] -- 63 uniform 6-polytopes as permutations of rings in the group diagram, including two regular forms:
- {4,33} — 6-cube (hexeract) -
- {33,4} — 6-orthoplex, (hexacross) -
- 63 uniform 6-polytopes as permutations of rings in the group diagram, including two regular forms:
- Demihypercube D6 family: [33,1,1] -
- 47 uniform 6-polytopes (16 unique) as permutations of rings in the group diagram, including:
- {3,32,1}, 121 6-demicube (demihexeract) - ; also as h{4,33},
- {3,3,31,1}, 211 6-orthoplex -
- 47 uniform 6-polytopes (16 unique) as permutations of rings in the group diagram, including:
- E6 family: [33,1,1] -
- 39 uniform 6-polytopes (16 unique) as permutations of rings in the group diagram, including:
- {3,3,32,1}, 221Gosset 2 21 polytopeIn 6-dimensional geometry, the 221 polytope is a uniform 6-polytope, constructed within the symmetry of the E6 group. It was discovered by Thorold Gosset, published in his 1900 paper. He called it an 6-ic semi-regular figure....
- - {3,32,2}, 122Gosset 1 22 polytopeIn 6-dimensional geometry, the 122 polytope is a uniform polytope, constructed from the E6 group. It was first published in E. L. Elte's 1912 listing of semiregular polytopes, named as V72 ....
-
- {3,3,32,1}, 221
- 39 uniform 6-polytopes (16 unique) as permutations of rings in the group diagram, including:
These fundamental families generate 153 nonprismatic convex uniform polypeta.
In addition, there are 105 uniform 6-polytope constructions based on prisms of the uniform polyteron
Uniform polyteron
In geometry, a uniform polyteron is a five-dimensional uniform polytope. By definition, a uniform polyteron is vertex-transitive and constructed from uniform polychoron facets....
s: [3,3,3,3]x[ ], [4,3,3,3]x[ ], [5,3,3,3]x[ ], [32,1,1]x[ ].
In addition, there are infinitely many uniform 6-polytope based on:
- Duoprism prism families: [3,3]x[p]x[ ], [4,3]x[p]x[ ], [5,3]x[p]x[ ].
- Duoprism families: [3,3,3]x[p], [4,3,3]x[p], [5,3,3]x[p].
- Triaprism family: [p]x[q]x[r].
The A6 family
There are 32+4−1=35 forms, derived by marking one or more nodes of the Coxeter-Dynkin diagramCoxeter-Dynkin diagram
In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors...
.
All 35 are enumerated below. They are named by Norman Johnson from the Wythoff construction operations upon regular 6-simplex (heptapeton). Bowers-style acronym names are given in parentheses for cross-referencing.
The A6 family has symmetry of order 5040 (7 factorial
Factorial
In mathematics, the factorial of a non-negative integer n, denoted by n!, is the product of all positive integers less than or equal to n...
).
The coordinates of uniform 6-polytopes with 6-simplex symmetry can be generated as permutations of simple integers in 7-space, all in hyperplanes with normal vector (1,1,1,1,1,1,1).
See also list of A6 polytopes for graphs of these polytopes.
| # | Coxeter-Dynkin Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... |
Johnson naming system Bowers name and (acronym) |
Base point | Element counts | |||||
|---|---|---|---|---|---|---|---|---|---|
| 5 | 4 | 3 | 2 | 1 | 0 | ||||
| 1 | 6-simplex heptapeton (hop) |
(0,0,0,0,0,0,1) | 7 | 21 | 35 | 35 | 21 | 7 | |
| 2 | Rectified 6-simplex Rectified 6-simplex In six-dimensional geometry, a rectified 6-simplex is a convex uniform 6-polytope, being a rectification of the regular 6-simplex.There are three unique degrees of rectifications, including the zeroth, the 6-simplex itself. Vertices of the rectified 6-simplex are located at the edge-centers of the... rectified heptapeton (ril) |
(0,0,0,0,0,1,1) | 14 | 63 | 140 | 175 | 105 | 21 | |
| 3 | Truncated 6-simplex Truncated 6-simplex In six-dimensional geometry, a truncated 6-simplex is a convex uniform 6-polytope, being a truncation of the regular 6-simplex.There are unique 3 degrees of truncation. Vertices of the truncation 6-simplex are located as pairs on the edge of the 6-simplex. Vertices of the bitruncated 6-simplex are... truncated heptapeton (til) |
(0,0,0,0,0,1,2) | 14 | 63 | 140 | 175 | 126 | 42 | |
| 4 | Birectified 6-simplex birectified heptapeton (bril) |
(0,0,0,0,1,1,1) | 14 | 84 | 245 | 350 | 210 | 35 | |
| 5 | Cantellated 6-simplex Cantellated 6-simplex In six-dimensional geometry, a cantellated 6-simplex is a convex uniform 6-polytope, being a cantellation of the regular 6-simplex.There are unique 4 degrees of cantellation for the 6-simplex, including truncations.- Cantellated 6-simplex:... small rhombated heptapeton (sril) |
(0,0,0,0,1,1,2) | 35 | 210 | 560 | 805 | 525 | 105 | |
| 6 | Bitruncated 6-simplex bitruncated heptapeton (batal) |
(0,0,0,0,1,2,2) | 14 | 84 | 245 | 385 | 315 | 105 | |
| 7 | Cantitruncated 6-simplex great rhombated heptapeton (gril) |
(0,0,0,0,1,2,3) | 35 | 210 | 560 | 805 | 630 | 210 | |
| 8 | Runcinated 6-simplex Runcinated 6-simplex In six-dimensional geometry, a runcinated 6-simplex is a convex uniform 6-polytope constructed as a runcination of the regular 6-simplex.... small prismated heptapeton (spil) |
(0,0,0,1,1,1,2) | 70 | 455 | 1330 | 1610 | 840 | 140 | |
| 9 | Bicantellated 6-simplex small prismated heptapeton (sabril) |
(0,0,0,1,1,2,2) | 70 | 455 | 1295 | 1610 | 840 | 140 | |
| 10 | Runcitruncated 6-simplex prismatotruncated heptapeton (patal) |
(0,0,0,1,1,2,3) | 70 | 560 | 1820 | 2800 | 1890 | 420 | |
| 11 | Tritruncated 6-simplex tetradecapeton (fe) |
(0,0,0,1,2,2,2) | 14 | 84 | 280 | 490 | 420 | 140 | |
| 12 | Runcicantellated 6-simplex prismatorhombated heptapeton (pril) |
(0,0,0,1,2,2,3) | 70 | 455 | 1295 | 1960 | 1470 | 420 | |
| 13 | Bicantitruncated 6-simplex great birhombated heptapeton (gabril) |
(0,0,0,1,2,3,3) | 49 | 329 | 980 | 1540 | 1260 | 420 | |
| 14 | Runcicantitruncated 6-simplex great prismated heptapeton (gapil) |
(0,0,0,1,2,3,4) | 70 | 560 | 1820 | 3010 | 2520 | 840 | |
| 15 | Stericated 6-simplex Stericated 6-simplex In six-dimensional geometry, a stericated 6-simplex is a convex uniform 6-polytope with 4th order truncations of the regular 6-simplex.... small cellated heptapeton (scal) |
(0,0,1,1,1,1,2) | 105 | 700 | 1470 | 1400 | 630 | 105 | |
| 16 | Biruncinated 6-simplex small biprismato-tetradecapeton (sibpof) |
(0,0,1,1,1,2,2) | 84 | 714 | 2100 | 2520 | 1260 | 210 | |
| 17 | Steritruncated 6-simplex cellitruncated heptapeton (catal) |
(0,0,1,1,1,2,3) | 105 | 945 | 2940 | 3780 | 2100 | 420 | |
| 18 | Stericantellated 6-simplex cellirhombated heptapeton (cral) |
(0,0,1,1,2,2,3) | 105 | 1050 | 3465 | 5040 | 3150 | 630 | |
| 19 | Biruncitruncated 6-simplex biprismatorhombated heptapeton (bapril) |
(0,0,1,1,2,3,3) | 84 | 714 | 2310 | 3570 | 2520 | 630 | |
| 20 | Stericantitruncated 6-simplex celligreatorhombated heptapeton (cagral) |
(0,0,1,1,2,3,4) | 105 | 1155 | 4410 | 7140 | 5040 | 1260 | |
| 21 | Steriruncinated 6-simplex celliprismated heptapeton (copal) |
(0,0,1,2,2,2,3) | 105 | 700 | 1995 | 2660 | 1680 | 420 | |
| 22 | Steriruncitruncated 6-simplex celliprismatotruncated heptapeton (captal) |
(0,0,1,2,2,3,4) | 105 | 945 | 3360 | 5670 | 4410 | 1260 | |
| 23 | Steriruncicantellated 6-simplex celliprismatorhombated heptapeton (copril) |
(0,0,1,2,3,3,4) | 105 | 1050 | 3675 | 5880 | 4410 | 1260 | |
| 24 | Biruncicantitruncated 6-simplex great biprismato-tetradecapeton (gibpof) |
(0,0,1,2,3,4,4) | 84 | 714 | 2520 | 4410 | 3780 | 1260 | |
| 25 | Steriruncicantitruncated 6-simplex great cellated heptapeton (gacal) |
(0,0,1,2,3,4,5) | 105 | 1155 | 4620 | 8610 | 7560 | 2520 | |
| 26 | Pentellated 6-simplex Pentellated 6-simplex In six-dimensional geometry, a pentellated 6-simplex is a convex uniform 6-polytope with 5th order truncations of the regular 6-simplex.There are unique 10 degrees of pentellations of the 6-simplex with permutations of truncations, cantellations, runcinations, and sterications... small teri-tetradecapeton (staf) |
(0,1,1,1,1,1,2) | 126 | 434 | 630 | 490 | 210 | 42 | |
| 27 | Pentitruncated 6-simplex teracellated heptapeton (tocal) |
(0,1,1,1,1,2,3) | 126 | 826 | 1785 | 1820 | 945 | 210 | |
| 28 | Penticantellated 6-simplex teriprismated heptapeton (topal) |
(0,1,1,1,2,2,3) | 126 | 1246 | 3570 | 4340 | 2310 | 420 | |
| 29 | Penticantitruncated 6-simplex terigreatorhombated heptapeton (togral) |
(0,1,1,1,2,3,4) | 126 | 1351 | 4095 | 5390 | 3360 | 840 | |
| 30 | Pentiruncitruncated 6-simplex tericellirhombated heptapeton (tocral) |
(0,1,1,2,2,3,4) | 126 | 1491 | 5565 | 8610 | 5670 | 1260 | |
| 31 | Pentiruncicantellated 6-simplex teriprismatorhombi-tetradecapeton (taporf) |
(0,1,1,2,3,3,4) | 126 | 1596 | 5250 | 7560 | 5040 | 1260 | |
| 32 | Pentiruncicantitruncated 6-simplex terigreatoprismated heptapeton (tagopal) |
(0,1,1,2,3,4,5) | 126 | 1701 | 6825 | 11550 | 8820 | 2520 | |
| 33 | Pentisteritruncated 6-simplex tericellitrunki-tetradecapeton (tactaf) |
(0,1,2,2,2,3,4) | 126 | 1176 | 3780 | 5250 | 3360 | 840 | |
| 34 | Pentistericantitruncated 6-simplex tericelligreatorhombated heptapeton (tacogral) |
(0,1,2,2,3,4,5) | 126 | 1596 | 6510 | 11340 | 8820 | 2520 | |
| 35 | Omnitruncated 6-simplex great teri-tetradecapeton (gotaf) |
(0,1,2,3,4,5,6) | 126 | 1806 | 8400 | 16800 | 15120 | 5040 | |
The B6 family
There are 63 forms based on all permutations of the Coxeter-Dynkin diagramCoxeter-Dynkin diagram
In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors...
s with one or more rings.
The B6 family has symmetry of order 46080 (6 factorial
Factorial
In mathematics, the factorial of a non-negative integer n, denoted by n!, is the product of all positive integers less than or equal to n...
x 26).
They are named by Norman Johnson from the Wythoff construction operations upon the regular 6-cube and 6-orthoplex. Bowers names and acronym names are given for cross-referencing.
See also list of B6 polytopes for graphs of these polytopes.
| # | Coxeter-Dynkin diagram Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... |
Schläfli symbol | Names | Element counts | |||||
|---|---|---|---|---|---|---|---|---|---|
| 5 | 4 | 3 | 2 | 1 | 0 | ||||
| 36 | t0{3,3,3,3,4} | 6-orthoplex Hexacontatetrapeton (gee) |
64 | 192 | 240 | 160 | 60 | 12 | |
| 37 | t1{3,3,3,3,4} | Rectified 6-orthoplex Rectified hexacontatetrapeton (rag) |
76 | 576 | 1200 | 1120 | 480 | 60 | |
| 38 | t2{3,3,3,3,4} | Birectified 6-orthoplex Birectified hexacontatetrapeton (brag) |
76 | 636 | 2160 | 2880 | 1440 | 160 | |
| 39 | t2{4,3,3,3,3} | Birectified 6-cube Birectified hexeract (brox) |
76 | 636 | 2080 | 3200 | 1920 | 240 | |
| 40 | t1{4,3,3,3,3} | Rectified 6-cube Rectified 6-cube In six-dimensional geometry, a rectified 6-cube is a convex uniform 6-polytope, being a rectification of the regular 6-cube.There are unique 6 degrees of rectifications, the zeroth being the 6-cube, and the 6th and last being the 6-orthoplex. Vertices of the rectified 6-cube are located at the... Rectified hexeract (rax) |
76 | 576 | 1200 | 1120 | 480 | 60 | |
| 41 | t0{4,3,3,3,3} | 6-cube Hexeract (ax) |
12 | 60 | 160 | 240 | 192 | 64 | |
| 42 | t0,1{3,3,3,3,4} | Truncated 6-orthoplex Truncated 6-orthoplex In six-dimensional geometry, a truncated 6-orthoplex is a convex uniform 6-polytope, being a truncation of the regular 6-orthoplex.There are 5 degrees of truncation for the 6-orthoplex. Vertices of the truncated 6-orthoplex are located as pairs on the edge of the 6-orthoplex. Vertices of the... Truncated hexacontatetrapeton (tag) |
76 | 576 | 1200 | 1120 | 540 | 120 | |
| 43 | t0,2{3,3,3,3,4} | Cantellated 6-orthoplex Cantellated 6-orthoplex In six-dimensional geometry, a cantellated 6-orthoplex is a convex uniform 6-polytope, being a cantellation of the regular 6-orthoplex.There are 8 cantellation for the 6-orthoplex including truncations... Small rhombated hexacontatetrapeton (srog) |
136 | 1656 | 5040 | 6400 | 3360 | 480 | |
| 44 | t1,2{3,3,3,3,4} | Bitruncated 6-orthoplex Bitruncated hexacontatetrapeton (botag) |
1920 | 480 | |||||
| 45 | t0,3{3,3,3,3,4} | Runcinated 6-orthoplex Runcinated 6-orthoplex In six-dimensional geometry, a runcinated 6-orthplex is a convex uniform 6-polytope with 3rd order truncations of the regular 6-orthoplex.There are 12 unique runcinations of the 6-orthoplex with permutations of truncations, and cantellations... Small prismated hexacontatetrapeton (spog) |
7200 | 960 | |||||
| 46 | t1,3{3,3,3,3,4} | Bicantellated 6-orthoplex Small birhombated hexacontatetrapeton (siborg) |
8640 | 1440 | |||||
| 47 | t2,3{4,3,3,3,3} | Tritruncated 6-cube Hexeractihexacontitetrapeton (xog) |
3360 | 960 | |||||
| 48 | t0,4{3,3,3,3,4} | Stericated 6-orthoplex Stericated 6-orthoplex In six-dimensional geometry, a stericated 6-orthoplex is a convex uniform 6-polytope, constructed as a sterication of the regular 6-orthoplex.... Small cellated hexacontatetrapeton (scag) |
5760 | 960 | |||||
| 49 | t1,4{4,3,3,3,3} | Biruncinated 6-cube Small biprismato-hexeractihexacontitetrapeton (sobpoxog) |
11520 | 1920 | |||||
| 50 | t1,3{4,3,3,3,3} | Bicantellated 6-cube Small birhombated hexeract (saborx) |
9600 | 1920 | |||||
| 51 | t1,2{4,3,3,3,3} | Bitruncated 6-cube Bitruncated hexeract (botox) |
2880 | 960 | |||||
| 52 | t0,5{4,3,3,3,3} | Pentellated 6-cube Pentellated 6-cube In six-dimensional geometry, a pentellated 6-cube is a convex uniform 6-polytope with 5th order truncations of the regular 6-cube.There are unique 16 degrees of pentellations of the 6-cube with permutations of truncations, cantellations, runcinations, and sterications... Small teri-hexeractihexacontitetrapeton (stoxog) |
1920 | 384 | |||||
| 53 | t0,4{4,3,3,3,3} | Stericated 6-cube Stericated 6-cube In six-dimensional geometry, a stericated 6-cube is a convex uniform 6-polytope, constructed as a sterication of the regular 6-cube.... Small cellated hexeract (scox) |
5760 | 960 | |||||
| 54 | t0,3{4,3,3,3,3} | Runcinated 6-cube Runcinated 6-cube In six-dimensional geometry, a runcinated 6-cube is a convex uniform 6-polytope with 3rd order truncations of the regular 6-cube.There are 12 unique runcinations of the 6-cube with permutations of truncations, and cantellations... Small prismated hexeract (spox) |
7680 | 1280 | |||||
| 55 | t0,2{4,3,3,3,3} | Cantellated 6-cube Cantellated 6-cube In six-dimensional geometry, a cantellated 6-cube is a convex uniform 6-polytope, being a cantellation of the regular 6-cube.There are 8 cantellations for the 6-cube, including truncations... Small rhombated hexeract (srox) |
4800 | 960 | |||||
| 56 | t0,1{4,3,3,3,3} | Truncated 6-cube Truncated hexeract (tox) |
76 | 444 | 1120 | 1520 | 1152 | 384 | |
| 57 | t0,1,2{3,3,3,3,4} | Cantitruncated 6-orthoplex Great rhombated hexacontatetrapeton (grog) |
3840 | 960 | |||||
| 58 | t0,1,3{3,3,3,3,4} | Runcitruncated 6-orthoplex Prismatotruncated hexacontatetrapeton (potag) |
15840 | 2880 | |||||
| 59 | t0,2,3{3,3,3,3,4} | Runcicantellated 6-orthoplex Prismatorhombated hexacontatetrapeton (prog) |
11520 | 2880 | |||||
| 60 | t1,2,3{3,3,3,3,4} | Bicantitruncated 6-orthoplex Great birhombated hexacontatetrapeton (gaborg) |
10080 | 2880 | |||||
| 61 | t0,1,4{3,3,3,3,4} | Steritruncated 6-orthoplex Cellitruncated hexacontatetrapeton (catog) |
19200 | 3840 | |||||
| 62 | t0,2,4{3,3,3,3,4} | Stericantellated 6-orthoplex Cellirhombated hexacontatetrapeton (crag) |
28800 | 5760 | |||||
| 63 | t1,2,4{3,3,3,3,4} | Biruncitruncated 6-orthoplex Biprismatotruncated hexacontatetrapeton (boprax) |
23040 | 5760 | |||||
| 64 | t0,3,4{3,3,3,3,4} | Steriruncinated 6-orthoplex Celliprismated hexacontatetrapeton (copog) |
15360 | 3840 | |||||
| 65 | t1,2,4{4,3,3,3,3} | Biruncitruncated 6-cube Biprismatotruncated hexeract (boprag) |
23040 | 5760 | |||||
| 66 | t1,2,3{4,3,3,3,3} | Bicantitruncated 6-cube Great birhombated hexeract (gaborx) |
11520 | 3840 | |||||
| 67 | t0,1,5{3,3,3,3,4} | Pentitruncated 6-orthoplex Teritruncated hexacontatetrapeton (tacox) |
8640 | 1920 | |||||
| 68 | t0,2,5{3,3,3,3,4} | Penticantellated 6-orthoplex Terirhombated hexacontatetrapeton (tapox) |
21120 | 3840 | |||||
| 69 | t0,3,4{4,3,3,3,3} | Steriruncinated 6-cube Celliprismated hexeract (copox) |
15360 | 3840 | |||||
| 70 | t0,2,5{4,3,3,3,3} | Penticantellated 6-cube Terirhombated hexeract (topag) |
21120 | 3840 | |||||
| 71 | t0,2,4{4,3,3,3,3} | Stericantellated 6-cube Cellirhombated hexeract (crax) |
28800 | 5760 | |||||
| 72 | t0,2,3{4,3,3,3,3} | Runcicantellated 6-cube Prismatorhombated hexeract (prox) |
13440 | 3840 | |||||
| 73 | t0,1,5{4,3,3,3,3} | Pentitruncated 6-cube Teritruncated hexeract (tacog) |
8640 | 1920 | |||||
| 74 | t0,1,4{4,3,3,3,3} | Steritruncated 6-cube Cellitruncated hexeract (catax) |
19200 | 3840 | |||||
| 75 | t0,1,3{4,3,3,3,3} | Runcitruncated 6-cube Prismatotruncated hexeract (potax) |
17280 | 3840 | |||||
| 76 | t0,1,2{4,3,3,3,3} | Cantitruncated 6-cube Great rhombated hexeract (grox) |
5760 | 1920 | |||||
| 77 | t0,1,2,3{3,3,3,3,4} | Runcicantitruncated 6-orthoplex Great prismated hexacontatetrapeton (gopog) |
20160 | 5760 | |||||
| 78 | t0,1,2,4{3,3,3,3,4} | Stericantitruncated 6-orthoplex Celligreatorhombated hexacontatetrapeton (cagorg) |
46080 | 11520 | |||||
| 79 | t0,1,3,4{3,3,3,3,4} | Steriruncitruncated 6-orthoplex Celliprismatotruncated hexacontatetrapeton (captog) |
40320 | 11520 | |||||
| 80 | t0,2,3,4{3,3,3,3,4} | Steriruncicantellated 6-orthoplex Celliprismatorhombated hexacontatetrapeton (coprag) |
40320 | 11520 | |||||
| 81 | t1,2,3,4{4,3,3,3,3} | Biruncicantitruncated 6-cube Great biprismato-hexeractihexacontitetrapeton (gobpoxog) |
34560 | 11520 | |||||
| 82 | t0,1,2,5{3,3,3,3,4} | Penticantitruncated 6-orthoplex Terigreatorhombated hexacontatetrapeton (togrig) |
30720 | 7680 | |||||
| 83 | t0,1,3,5{3,3,3,3,4} | Pentiruncitruncated 6-orthoplex Teriprismatotruncated hexacontatetrapeton (tocrax) |
51840 | 11520 | |||||
| 84 | t0,2,3,5{4,3,3,3,3} | Pentiruncicantellated 6-cube Teriprismatorhombi-hexeractihexacontitetrapeton (tiprixog) |
46080 | 11520 | |||||
| 85 | t0,2,3,4{4,3,3,3,3} | Steriruncicantellated 6-cube Celliprismatorhombated hexeract (coprix) |
40320 | 11520 | |||||
| 86 | t0,1,4,5{4,3,3,3,3} | Pentisteritruncated 6-cube Tericelli-hexeractihexacontitetrapeton (tactaxog) |
30720 | 7680 | |||||
| 87 | t0,1,3,5{4,3,3,3,3} | Pentiruncitruncated 6-cube Teriprismatotruncated hexeract (tocrag) |
51840 | 11520 | |||||
| 88 | t0,1,3,4{4,3,3,3,3} | Steriruncitruncated 6-cube Celliprismatotruncated hexeract (captix) |
40320 | 11520 | |||||
| 89 | t0,1,2,5{4,3,3,3,3} | Penticantitruncated 6-cube Terigreatorhombated hexeract (togrix) |
30720 | 7680 | |||||
| 90 | t0,1,2,4{4,3,3,3,3} | Stericantitruncated 6-cube Celligreatorhombated hexeract (cagorx) |
46080 | 11520 | |||||
| 91 | t0,1,2,3{4,3,3,3,3} | Runcicantitruncated 6-cube Great prismated hexeract (gippox) |
23040 | 7680 | |||||
| 92 | t0,1,2,3,4{3,3,3,3,4} | Steriruncicantitruncated 6-orthoplex Great cellated hexacontatetrapeton (gocog) |
69120 | 23040 | |||||
| 93 | t0,1,2,3,5{3,3,3,3,4} | Pentiruncicantitruncated 6-orthoplex Terigreatoprismated hexacontatetrapeton (tagpog) |
80640 | 23040 | |||||
| 94 | t0,1,2,4,5{3,3,3,3,4} | Pentistericantitruncated 6-orthoplex Tericelligreatorhombated hexacontatetrapeton (tecagorg) |
80640 | 23040 | |||||
| 95 | t0,1,2,4,5{4,3,3,3,3} | Pentistericantitruncated 6-cube Tericelligreatorhombated hexeract (tocagrax) |
80640 | 23040 | |||||
| 96 | t0,1,2,3,5{4,3,3,3,3} | Pentiruncicantitruncated 6-cube Terigreatoprismated hexeract (tagpox) |
80640 | 23040 | |||||
| 97 | t0,1,2,3,4{4,3,3,3,3} | Steriruncicantitruncated 6-cube Great cellated hexeract (gocax) |
69120 | 23040 | |||||
| 98 | t0,1,2,3,4,5{4,3,3,3,3} | Omnitruncated 6-cube Great teri-hexeractihexacontitetrapeton (gotaxog) |
138240 | 46080 |
The D6 family
The D6 family has symmetry of order 23040 (6 factorialFactorial
In mathematics, the factorial of a non-negative integer n, denoted by n!, is the product of all positive integers less than or equal to n...
x 25).
This family has 3×16−1=47 Wythoffian uniform polytopes, generated by marking one or more nodes of the D6 Coxeter-Dynkin diagram
Coxeter-Dynkin diagram
In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors...
. Of these, 31 (2×16−1) are repeated from the B6 family and 16 are unique to this family. The 16 unique forms are enumerated below. Bowers-style acronym names are given for cross-referencing.
See list of D6 polytopes for Coxeter plane graphs of these polytopes.
| # | Coxeter-Dynkin diagram Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... |
Names | Base point (Alternately signed) |
Element counts | Circumrad | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| 5 | 4 | 3 | 2 | 1 | 0 | |||||
| 99 | 6-demicube Hemihexeract (hax) |
(1,1,1,1,1,1) | 44 | 252 | 640 | 640 | 240 | 32 | 0.8660254 | |
| 100 | Truncated 6-demicube Truncated hemihexeract (thax) |
(1,1,3,3,3,3) | 76 | 636 | 2080 | 3200 | 2160 | 480 | 2.1794493 | |
| 101 | Cantellated 6-demicube Cantellated 6-demicube In six-dimensional geometry, a cantellated 6-demicube is a convex uniform 6-polytope, being a cantellation of the uniform 6-demicube. There are 2 unique cantellation for the 6-demicube including a truncation.- Cantellated 6-demicube:... Small rhombated hemihexeract (sirhax) |
(1,1,1,3,3,3) | 3840 | 640 | 1.9364916 | |||||
| 102 | Runcinated 6-demicube Runcinated 6-demicube In six-dimensional geometry, a runcinated 6-demicube is a convex uniform 6-polytope with 3rd order truncations of the uniform 6-demicube.There are unique 4 runcinations of the 6-demicube, including permutations of truncations, and cantellations.... Small prismated hemihexeract (sophax) |
(1,1,1,1,3,3) | 3360 | 480 | 1.6583123 | |||||
| 103 | Stericated 6-demicube Stericated 6-demicube In six-dimensional geometry, a stericated 6-demicube is a convex uniform 6-polytope, constructed as a sterication of the 6-demicube.... Small cellated demihexeract (sochax) |
(1,1,1,1,1,3) | 1440 | 192 | 1.3228756 | |||||
| 104 | Cantitruncated 6-demicube Great rhombated hemihexeract (girhax) |
(1,1,3,5,5,5) | 5760 | 1920 | 3.2787192 | |||||
| 105 | Runcitruncated 6-demicube Prismatotruncated hemihexeract (pithax) |
(1,1,3,3,5,5) | 12960 | 2880 | 2.95804 | |||||
| 106 | Runcicantellated 6-demicube Prismatorhombated hemihexeract (prohax) |
(1,1,1,3,5,5) | 7680 | 1920 | 2.7838821 | |||||
| 107 | Steritruncated 6-demicube Cellitruncated hemihexeract (cathix) |
(1,1,3,3,3,5) | 9600 | 1920 | 2.5980761 | |||||
| 108 | Stericantellated 6-demicube Cellirhombated hemihexeract (crohax) |
(1,1,1,3,3,5) | 10560 | 1920 | 2.3979158 | |||||
| 109 | Steriruncinated 6-demicube Celliprismated hemihexeract (cophix) |
(1,1,1,1,3,5) | 5280 | 960 | 2.1794496 | |||||
| 110 | Runcicantitruncated 6-demicube Great prismated hemihexeract (gophax) |
(1,1,3,5,7,7) | 17280 | 5760 | 4.0926762 | |||||
| 111 | Stericantitruncated 6-demicube Celligreatorhombated hemihexeract (cagrohax) |
(1,1,3,5,5,7) | 20160 | 5760 | 3.7080991 | |||||
| 112 | Steriruncitruncated 6-demicube Celliprismatotruncated hemihexeract (capthix) |
(1,1,3,3,5,7) | 23040 | 5760 | 3.4278274 | |||||
| 113 | Steriruncicantellated 6-demicube Celliprismatorhombated hemihexeract (caprohax) |
(1,1,1,3,5,7) | 15360 | 3840 | 3.2787192 | |||||
| 114 | Steriruncicantitruncated 6-demicube Great cellated hemihexeract (gochax) |
(1,1,3,5,7,9) | 34560 | 11520 | 4.5552168 |
The E6 family
There are 39 forms based on all permutations of the Coxeter-Dynkin diagramCoxeter-Dynkin diagram
In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors...
s with one or more rings. Bowers-style acronym names are given for cross-referencing. The E6 family has symmetry of order 51,840.
See also list of E6 polytopes for graphs of these polytopes.
| # | Coxeter-Dynkin diagram Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... Schläfli symbol |
Names | Element counts | |||||
|---|---|---|---|---|---|---|---|---|
| 5-faces | 4-faces | Cells | Faces | Edges | Vertices | |||
| 115 | 221 Icosiheptaheptacontidipeton (jak) |
99 | 648 | 1080 | 720 | 216 | 27 | |
| 116 | Rectified 221 Rectified icosiheptaheptacontidipeton (rojak) |
126 | 1350 | 4320 | 5040 | 2160 | 216 | |
| 117 | Rectified 122 Rectified pentacontatetrapeton (ram) |
126 | 1566 | 6480 | 10800 | 6480 | 720 | |
| 118 | 122 Pentacontatetrapeton (mo) |
54 | 702 | 2160 | 2160 | 720 | 72 | |
| 119 | Truncated 221 Truncated icosiheptaheptacontidipeton (tojak) |
126 | 1350 | 4320 | 5040 | 2376 | 432 | |
| 120 | Cantellated 221 Small rhombated icosiheptaheptacontidipeton (sirjak) |
342 | 3942 | 15120 | 24480 | 15120 | 2160 | |
| 121 | Runcinated 221 Small demiprismated icosiheptaheptacontidipeton (shopjak) |
342 | 4662 | 16200 | 19440 | 8640 | 1080 | |
| 122 | Stericated 221 Trirectified pentacontatetrapeton (trim) |
558 | 4608 | 8640 | 6480 | 2160 | 270 | |
| 123 | Demified icosiheptaheptacontidipeton (hejak) | 342 | 2430 | 7200 | 7920 | 3240 | 432 | |
| 124 | Bitruncated 221 Bitruncated icosiheptaheptacontidipeton (botajik) |
2160 | ||||||
| 125 | Bicantellated 221 Birectified pentacontatetrapeton (barm) |
12960 | 2160 | |||||
| 126 | Demirectified icosiheptaheptacontidipeton (harjak) | 1080 | ||||||
| 127 | Truncated pentacontatetrapeton (tim) | 13680 | 1440 | |||||
| 128 | Cantitruncated 221 Great rhombated icosiheptaheptacontidipeton (girjak) |
4320 | ||||||
| 129 | Runcitruncated 221 Demiprismatotruncated icosiheptaheptacontidipeton (hopitjak) |
4320 | ||||||
| 130 | Steritruncated 221 Cellitruncated icosiheptaheptacontidipeton (catjak) |
2160 | ||||||
| 131 | Demitruncated icosiheptaheptacontidipeton (hotjak) | 2160 | ||||||
| 132 | Runcicantellated 221 Demiprismatorhombated icosiheptaheptacontidipeton (haprojak) |
6480 | ||||||
| 133 | Stericantellated 221 Small birhombated pentacontatetrapeton (sabrim) |
6480 | ||||||
| 134 | Small demirhombated icosiheptaheptacontidipeton (shorjak) | 4320 | ||||||
| 135 | Small prismated icosiheptaheptacontidipeton (spojak) | 4320 | ||||||
| 136 | Small prismated pentacontatetrapeton (spam) | 2160 | ||||||
| 137 | Bitruncated pentacontatetrapeton (bitem) | 6480 | ||||||
| 138 | Tritruncated icosiheptaheptacontidipeton (titajak) | 4320 | ||||||
| 139 | Small rhombated pentacontatetrapeton (sram) | 6480 | ||||||
| 140 | Runcicantitruncated 221 Great demiprismated icosiheptaheptacontidipeton (ghopjak) |
12960 | ||||||
| 141 | Stericantitruncated 221 Celligreatorhombated icosiheptaheptacontidipeton (cograjik) |
12960 | ||||||
| 142 | Great demirhombated icosiheptaheptacontidipeton (ghorjak) | 8640 | ||||||
| 143 | Steriruncitruncated 221 Tritruncated pentacontatetrapeton (titam) |
8640 | ||||||
| 144 | Prismatotruncated icosiheptaheptacontidipeton (potjak) | 12960 | ||||||
| 145 | Demicellitruncated icosiheptaheptacontidipeton (hictijik) | 8640 | ||||||
| 146 | Prismatorhombated icosiheptaheptacontidipeton (projak) | 12960 | ||||||
| 147 | Prismatotruncated pentacontatetrapeton (patom) | 12960 | ||||||
| 148 | Great rhombated pentacontatetrapeton (gram) | 12960 | ||||||
| 149 | Steriruncicantitruncated 221 Great birhombated pentacontatetrapeton (gabrim) |
25920 | ||||||
| 150 | Great prismated icosiheptaheptacontidipeton (gapjak) | 25920 | ||||||
| 151 | Demicelligreatorhombated icosiheptaheptacontidipeton (hocgarjik) | 25920 | ||||||
| 152 | Prismatorhombated pentacontatetrapeton (prom) | 25920 | ||||||
| 153 | Great prismated pentacontatetrapeton (gopam) | 51840 | ||||||
Regular and uniform honeycombs
There are four fundamental affine Coxeter groups and 27 prismatic groups that generate regular and uniform tessellations in 5-space:| # | Coxeter group Coxeter group In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example... |
Coxeter-Dynkin diagram Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... |
|
|---|---|---|---|
| 1 |  |
[3[6]] | |
| 2 |  |
h[4,33,4] [4,3,31,1] |
|
| 3 |  |
[4,33,4] | |
| 4 |  |
q[4,33,4] [31,1,3,31,1] |
|
| # | Coxeter group Coxeter group In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example... |
Coxeter-Dynkin diagram Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... |
|
|---|---|---|---|
| 1 |  x x |
[3[5]]x[∞]x[∞] | |
| 2 |  x x |
[4,3,31,1]x[∞] | |
| 3 |  x x |
[4,3,3,4]x[∞] | |
| 4 |  x x |
[31,1,1,1]x[∞] | |
| 5 |  x x |
[3,4,3,3]x[∞] | |
| 6 |  x x x x |
[4,3,4]x[∞]x[∞] | |
| 7 |  x x x x |
[4,31,1]x[∞]x[∞] | |
| 8 |  x x x x |
[3[4]]x[∞]x[∞] | |
| 9 |  x x x x x x |
[4,4]x[∞]x[∞]x[∞] | |
| 10 |  x x x x x x |
[6,3]x[∞]x[∞]x[∞] | |
| 11 |  x x x x x x |
[3[3]]x[∞]x[∞]x[∞] | |
| 12 |  x x x x x x x x |
[∞]x[∞]x[∞]x[∞]x[∞] | |
| 13 |  x x x x |
[3[3]]x[3[3]]x[∞] | |
| 14 |  x x x x |
[3[3]]x[4,4]x[∞] | |
| 15 |  x x x x |
[3[3]]x[6,3]x[∞] | |
| 16 |  x x x x |
[4,4]x[4,4]x[∞] | |
| 17 |  x x x x |
[4,4]x[6,3]x[∞] | |
| 18 |  x x x x |
[6,3]x[6,3]x[∞] | |
| 19 |  x x |
[3[4]]x[3[3]] | |
| 20 |  x x |
[4,31,1]x[3[3]] | |
| 21 |  x x |
[4,3,4]x[3[3]] | |
| 22 |  x x |
[3[4]]x[4,4] | |
| 23 |  x x |
[4,31,1]x[4,4] | |
| 24 |  x x |
[4,3,4]x[4,4] | |
| 25 |  x x |
[3[4]]x[6,3] | |
| 26 |  x x |
[4,31,1]x[6,3] | |
| 27 |  x x |
[4,3,4]x[6,3] | |
Regular and uniform honeycombs include:
-

- Regular hypercube honeycomb of Euclidean 5-space, the penteractic honeycomb, with symbols {4,33,4}, =
-

- The uniform alternated hypercube honeycomb, demipenteractic honeycomb, with symbols h{4,33,4}, = =
-
 There are 12 unique uniform honeycombs, including:
There are 12 unique uniform honeycombs, including:
- 5-simplex honeycomb5-simplex honeycombIn five-dimensional Euclidean geometry, the 5-simplex honeycomb or hexateric honeycomb is a space-filling tessellation . Each vertex is shared by 12 5-simplexes, 30 rectified 5-simplexes, and 20 birectified 5-simplexes...
- Truncated 5-simplex honeycombTruncated 5-simplex honeycombIn five-dimensional Euclidean geometry, the truncated 5-simplex honeycomb or truncated hexateric honeycomb is a space-filling tessellation...
- Omnitruncated 5-simplex honeycombOmnitruncated 5-simplex honeycombIn five-dimensional Euclidean geometry, the omnitruncated 5-simplex honeycomb or omnitruncated hexateric honeycomb is a space-filling tessellation . It is composed entirely of omnitruncated 5-simplex facets....
- 5-simplex honeycomb
Regular and uniform hyperbolic honeycombs
There are no compact hyperbolic Coxeter groups of rank 6, groups that can generate honeycombs with all finite facets, and a finite vertex figureVertex figure
In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...
. However there are 12 noncompact hyperbolic Coxeter groups of rank 6, each generating uniform honeycombs in 5-space as permutations of rings of the Coxeter diagrams.
 = [3,3[5]]: = [3,3[5]]:  = [(3,3,3,3,3,4)]: = [(3,3,3,3,3,4)]:
|
 = [4,3,32,1]: = [4,3,32,1]:  = [3,4,31,1]: = [3,4,31,1]:  = [4,3,/3\,3,4]: = [4,3,/3\,3,4]: |
 = [3,3,3,4,3]: = [3,3,3,4,3]:  = [3,3,4,3,3]: = [3,3,4,3,3]:  = [3,4,3,3,4]: = [3,4,3,3,4]: |
 = [32,1,1,1]: = [32,1,1,1]:  = [4,3,31,1,1]: = [4,3,31,1,1]:  = [31,1,1,1,1]: = [31,1,1,1,1]: |
External links
- Polytope names
- Polytopes of Various Dimensions, Jonathan Bowers
- Multi-dimensional Glossary


 = [(3,3,4,3,3,4)]:
= [(3,3,4,3,3,4)]: