Duoprism - AbsoluteAstronomy.com

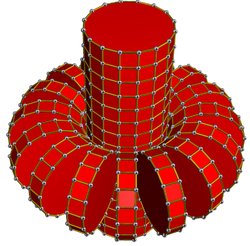
Set of uniform p,q-duoprisms Example 16,16-duoprism Schlegel diagram Projection from the center of one 16-gonal prism, and all but one of the opposite 16-gonal prisms are shown.
Type	Prismatic uniform polychoron
Schläfli symbol	{p}x{q}
Coxeter-Dynkin diagram Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors...
Cells	p q-gonal prisms Prism (geometry) In geometry, a prism is a polyhedron with an n-sided polygonal base, a translated copy , and n other faces joining corresponding sides of the two bases. All cross-sections parallel to the base faces are the same. Prisms are named for their base, so a prism with a pentagonal base is called a... , q p-gonal prisms
Faces	pq square Square (geometry) In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles... s, p q-gons, q p-gons
Edges	2pq
Vertices	pq
Vertex figure Vertex figure In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...	disphenoid tetrahedron
Symmetry Coxeter group In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example...	[p,2,q], order 4pq p,2,p, order 8p², p=q
Dual	Duopyramid
Properties	convex Convex polytope A convex polytope is a special case of a polytope, having the additional property that it is also a convex set of points in the n-dimensional space Rn... if both bases are convex

In geometry

Geometry

Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....

of 4 dimensions or higher, a duoprism is a polytope

Polytope

In elementary geometry, a polytope is a geometric object with flat sides, which exists in any general number of dimensions. A polygon is a polytope in two dimensions, a polyhedron in three dimensions, and so on in higher dimensions...

resulting from the Cartesian product

Cartesian product

In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...

of two polytopes, each of two dimensions or higher. The Cartesian product of an n-polytope and an m-polytope is an (n+m)-polytope, where n and m are 2 (polygon

Polygon

In geometry a polygon is a flat shape consisting of straight lines that are joined to form a closed chain orcircuit.A polygon is traditionally a plane figure that is bounded by a closed path, composed of a finite sequence of straight line segments...

) or higher.

The lowest dimensional duoprisms exist in 4-dimensional space as polychora

Polychoron

In geometry, a polychoron or 4-polytope is a four-dimensional polytope. It is a connected and closed figure, composed of lower dimensional polytopal elements: vertices, edges, faces , and cells...

(4-polytopes) being the Cartesian product

Cartesian product

of two polygon

Polygon

s in 2-dimensional Euclidean space

Euclidean space

In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...

. More precisely, it is the set of points:

where P₁ and P₂ are the sets of the points contained in the respective polygons. Such a duoprism is convex

Convex polytope

A convex polytope is a special case of a polytope, having the additional property that it is also a convex set of points in the n-dimensional space Rn...

if both bases are convex, and is bounded by prismatic cells

Prism (geometry)

In geometry, a prism is a polyhedron with an n-sided polygonal base, a translated copy , and n other faces joining corresponding sides of the two bases. All cross-sections parallel to the base faces are the same. Prisms are named for their base, so a prism with a pentagonal base is called a...

Nomenclature

Four-dimensional duoprisms are considered to be prismatic polychora. A duoprism constructed from two regular polygon

Regular polygon

A regular polygon is a polygon that is equiangular and equilateral . Regular polygons may be convex or star.-General properties:...

s of the same size is a uniform duoprism.

A duoprism made of n-polygons and m-polygons is named by prefixing 'duoprism' with the names of the base polygons, for example: a triangular-pentagonal duoprism is the Cartesian product of a triangle and a pentagon.

An alternative, more concise way of specifying a particular duoprism is by prefixing with numbers denoting the base polygons, for example: 3,5-duoprism for the triangular-pentagonal duoprism.

Other alternative names:

q-gonal-p-gonal prism
q-gonal-p-gonal double prism
q-gonal-p-gonal hyperprism

The term duoprism is coined by George Olshevsky

George Olshevsky

George Olshevsky is a freelance editor, writer, publisher, amateur paleontologist, and mathematician living in San Diego, California.Olshevsky maintains the comprehensive online Dinosaur Genera List...

, shortened from double prism. Conway

Conway

-Surname:* Alan Conway, impersonator of Stanley Kubrick* Albert Conway , Chief Judge of the New York Court of Appeals * Anne Conway, Viscountess Conway , English philosopher* Arthur Conway , any of several men...

proposed a similar name proprism for product prism.

Geometry of 4-dimensional duoprisms

A 4-dimensional uniform
Uniform polychoron
In geometry, a uniform polychoron is a polychoron or 4-polytope which is vertex-transitive and whose cells are uniform polyhedra....

duoprism is created by the product of a regular n-sided polygon

Polygon

and a regular m-sided polygon with the same edge length. It is bounded by n m-gonal prisms

Prism (geometry)

and m n-gonal prisms. For example, the Cartesian product of a triangle and a hexagon is a duoprism bounded by 6 triangular prisms and 3 hexagonal prisms.

When m and n are identical, the resulting duoprism is bounded by 2n identical n-gonal prisms. For example, the Cartesian product of two triangles is a duoprism bounded by 6 triangular prisms.

When m and n are identically 4, the resulting duoprism is bounded by 8 square prisms (cubes), and is identical to the tesseract
Tesseract
In geometry, the tesseract, also called an 8-cell or regular octachoron or cubic prism, is the four-dimensional analog of the cube. The tesseract is to the cube as the cube is to the square. Just as the surface of the cube consists of 6 square faces, the hypersurface of the tesseract consists of 8...

.

The m-gonal prisms are attached to each other via their m-gonal faces, and form a closed loop. Similarly, the n-gonal prisms are attached to each other via their n-gonal faces, and form a second loop perpendicular to the first. These two loops are attached to each other via their square faces, and are mutually perpendicular.

As m and n approach infinity, the corresponding duoprisms approach the duocylinder. As such, duoprisms are useful as non-quadric

Quadric

In mathematics, a quadric, or quadric surface, is any D-dimensional hypersurface in -dimensional space defined as the locus of zeros of a quadratic polynomial...

approximations of the duocylinder.

Polychoral duoantiprisms

Like the antiprism

Antiprism

In geometry, an n-sided antiprism is a polyhedron composed of two parallel copies of some particular n-sided polygon, connected by an alternating band of triangles...

s as alternated prism

Prism (geometry)

s, there is a set of 4-dimensional duoantiprisms polychoron

Polychoron

In geometry, a polychoron or 4-polytope is a four-dimensional polytope. It is a connected and closed figure, composed of lower dimensional polytopal elements: vertices, edges, faces , and cells...

s that can be created by an alternation operation applied to a duoprism. However most are not uniform. The alternated vertices create nonregular tetrahedral cells, except for the special case, the 4-4 duoprism (tesseract

Tesseract

In geometry, the tesseract, also called an 8-cell or regular octachoron or cubic prism, is the four-dimensional analog of the cube. The tesseract is to the cube as the cube is to the square. Just as the surface of the cube consists of 6 square faces, the hypersurface of the tesseract consists of 8...

) which creates the uniform (and regular) 16-cell

16-cell

In four dimensional geometry, a 16-cell or hexadecachoron is a regular convex 4-polytope. It is one of the six regular convex 4-polytopes first described by the Swiss mathematician Ludwig Schläfli in the mid-19th century....

. The 16-cell is the only convex uniform duoantiprism.

See also grand antiprism

Grand antiprism

In geometry, the grand antiprism or pentagonal double antiprismoid is a uniform polychoron bounded by 320 cells: 20 pentagonal antiprisms, and 300 tetrahedra. It is an anomalous, non-Wythoffian uniform polychoron, discovered in 1965 by Conway and Guy.- Alternate names :* Pentagonal double...

Related polytopes

The regular skew polyhedron

Regular skew polyhedron

In geometry, the regular skew polyhedra are generalizations to the set of regular polyhedron which include the possibility of nonplanar faces or vertex figures....

, {4,4|n}, exists in 4-space as the n² square faces of a n-n duoprism, using all 2n² edges and n² vertices. The 2n n-gonal faces can be seen as removed. (skew polyhedra can be seen in the same way by a n-m duoprism, but these are not regular.)

External links

The Fourth Dimension Simply Explained—describes duoprisms as "double prisms" and duocylinders as "double cylinders"
Polygloss - glossary of higher-dimensional terms
Exploring Hyperspace with the Geometric Product

The source of this article is wikipedia, the free encyclopedia. The text of this article is licensed under the GFDL.