
Antiprism
Encyclopedia
| Set of uniform antiprisms | |
|---|---|
 |
|
| Type | uniform polyhedron Uniform polyhedron A uniform polyhedron is a polyhedron which has regular polygons as faces and is vertex-transitive... |
| Faces | 2 n-gon Polygon In geometry a polygon is a flat shape consisting of straight lines that are joined to form a closed chain orcircuit.A polygon is traditionally a plane figure that is bounded by a closed path, composed of a finite sequence of straight line segments... s, 2n triangle Triangle A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted .... s |
| Edges | 4n |
| Vertices | 2n |
| Vertex configuration Vertex configuration In geometry, a vertex configuration is a short-hand notation for representing the vertex figure of a polyhedron or tiling as the sequence of faces around a vertex. For uniform polyhedra there is only one vertex type and therefore the vertex configuration fully defines the polyhedron... |
3.3.3.n |
| Schläfli symbol | h0,1{2,2n} s{2,n} |
| Coxeter-Dynkin diagram Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... s |
|
| Symmetry group | Dnd, [2+,2n], (2*n), order 4n Dn, [2,n]+, (22n), order 2n |
| Dual polyhedron Dual polyhedron In geometry, polyhedra are associated into pairs called duals, where the vertices of one correspond to the faces of the other. The dual of the dual is the original polyhedron. The dual of a polyhedron with equivalent vertices is one with equivalent faces, and of one with equivalent edges is another... |
trapezohedron Trapezohedron The n-gonal trapezohedron, antidipyramid or deltohedron is the dual polyhedron of an n-gonal antiprism. Its 2n faces are congruent kites . The faces are symmetrically staggered.The n-gon part of the name does not reference the faces here but arrangement of vertices around an axis of symmetry... |
| Properties | convex, semi-regular vertex-transitive Vertex-transitive In geometry, a polytope is isogonal or vertex-transitive if, loosely speaking, all its vertices are the same... |
| Net Net (polyhedron) In geometry the net of a polyhedron is an arrangement of edge-joined polygons in the plane which can be folded to become the faces of the polyhedron... |
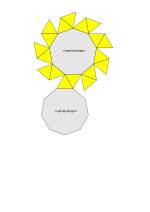 |
In geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, an n-sided antiprism is a polyhedron
Polyhedron
In elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...
composed of two parallel copies of some particular n-sided polygon
Polygon
In geometry a polygon is a flat shape consisting of straight lines that are joined to form a closed chain orcircuit.A polygon is traditionally a plane figure that is bounded by a closed path, composed of a finite sequence of straight line segments...
, connected by an alternating band of triangle
Triangle
A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....
s. Antiprisms are a subclass of the prismatoid
Prismatoid
In geometry, a prismatoid is a polyhedron where all vertices lie in two parallel planes....
s.
Antiprisms are similar to prism
Prism (geometry)
In geometry, a prism is a polyhedron with an n-sided polygonal base, a translated copy , and n other faces joining corresponding sides of the two bases. All cross-sections parallel to the base faces are the same. Prisms are named for their base, so a prism with a pentagonal base is called a...
s except the bases are twisted relative to each other, and that the side faces are triangles, rather than quadrilaterals.
In the case of a regular n-sided base, one usually considers the case where its copy is twisted by an angle 180°/n. Extra regularity is obtained by the line connecting the base centers being perpendicular to the base planes, making it a right antiprism. As faces, it has the two n-gonal bases and, connecting those bases, 2n isosceles triangles.
Uniform antiprism
A uniformPrismatic uniform polyhedron
In geometry, a prismatic uniform polyhedron is a uniform polyhedron with dihedral symmetry. They exist in two infinite families, the uniform prisms and the uniform antiprisms...
antiprism has, apart from the base faces, 2n equilateral triangles as faces. As a class, the uniform antiprisms form an infinite series of vertex-uniform polyhedra, as do the uniform prisms. For n=2 we have as degenerate case the regular tetrahedron
Tetrahedron
In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...
, and for n=3 the non-degenerate regular octahedron
Octahedron
In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....
.
The dual polyhedra
Dual polyhedron
In geometry, polyhedra are associated into pairs called duals, where the vertices of one correspond to the faces of the other. The dual of the dual is the original polyhedron. The dual of a polyhedron with equivalent vertices is one with equivalent faces, and of one with equivalent edges is another...
of the antiprisms are the trapezohedra
Trapezohedron
The n-gonal trapezohedron, antidipyramid or deltohedron is the dual polyhedron of an n-gonal antiprism. Its 2n faces are congruent kites . The faces are symmetrically staggered.The n-gon part of the name does not reference the faces here but arrangement of vertices around an axis of symmetry...
. Their existence was first discussed and their name was coined by Johannes Kepler
Johannes Kepler
Johannes Kepler was a German mathematician, astronomer and astrologer. A key figure in the 17th century scientific revolution, he is best known for his eponymous laws of planetary motion, codified by later astronomers, based on his works Astronomia nova, Harmonices Mundi, and Epitome of Copernican...
.
Cartesian coordinates
Cartesian coordinates for the vertices of a right antiprism with n-gonal bases and isosceles triangles arewith k ranging from 0 to 2n-1; if the triangles are equilateral,
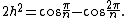
Volume and surface area
Let be the edge-length of a uniform
be the edge-length of a uniformUniform polyhedron
A uniform polyhedron is a polyhedron which has regular polygons as faces and is vertex-transitive...
antiprism. Then the volume is
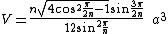
and the surface area is
Symmetry
The symmetry groupSymmetry group
The symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation...
of a right n-sided antiprism with regular base and isosceles side faces is Dnd of order 4n, except in the case of a tetrahedron, which has the larger symmetry group Td of order 24, which has three versions of D2d as subgroups, and the octahedron, which has the larger symmetry group Oh of order 48, which has four versions of D3d as subgroups.
The symmetry group contains inversion if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
n is odd.
The rotation group
Rotation group
In mechanics and geometry, the rotation group is the group of all rotations about the origin of three-dimensional Euclidean space R3 under the operation of composition. By definition, a rotation about the origin is a linear transformation that preserves length of vectors and preserves orientation ...
is Dn of order 2n, except in the case of a tetrahedron, which has the larger rotation group T of order 12, which has three versions of D2 as subgroups, and the octahedron, which has the larger rotation group O of order 24, which has four versions of D3 as subgroups.
See also
- Prismatic uniform polyhedronPrismatic uniform polyhedronIn geometry, a prismatic uniform polyhedron is a uniform polyhedron with dihedral symmetry. They exist in two infinite families, the uniform prisms and the uniform antiprisms...
- Triangular antiprism (OctahedronOctahedronIn geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....
) - Square antiprismSquare antiprismIn geometry, the square antiprism is the second in an infinite set of antiprisms formed by an even-numbered sequence of triangle sides closed by two polygon caps...
- Pentagonal antiprismPentagonal antiprismIn geometry, the pentagonal antiprism is the third in an infinite set of antiprisms formed by an even-numbered sequence of triangle sides closed by two polygon caps. It consists of two pentagons joined to each other by a ring of 10 triangles for a total of 12 faces...
- Hexagonal antiprismHexagonal antiprismIn geometry, the hexagonal antiprism is the 4th in an infinite set of antiprisms formed by an even-numbered sequence of triangle sides closed by two polygon caps.If faces are all regular, it is a semiregular polyhedron.- See also :* Set of antiprisms...
- Octagonal antiprismOctagonal antiprismIn geometry, the octagonal antiprism is the 6th in an infinite set of antiprisms formed by an even-numbered sequence of triangle sides closed by two polygon caps.If faces are all regular, it is a semiregular polyhedron.- See also :* Set of antiprisms...
- Decagonal antiprismDecagonal antiprismIn geometry, the decagonal antiprism is the eighth in an infinite set of antiprisms formed by an even-numbered sequence of triangle sides closed by two polygon caps.If faces are all regular, it is a semiregular polyhedron.- External links :*...
- Dodecagonal antiprismDodecagonal antiprismIn geometry, the dodecagonal antiprism is the tenth in an infinite set of antiprisms formed by an even-numbered sequence of triangle sides closed by two polygon caps.If faces are all regular, it is a semiregular polyhedron....
- Triangular antiprism (Octahedron
- Apeirogonal antiprismApeirogonal antiprismIn geometry, an apeirogonal antiprism or infinite antiprism is the arithmetic limit of the family of antiprisms; it can be considered an infinite polyhedron or a tiling of the plane.If the sides are equilateral triangles, it is a uniform tiling...
- Grand antiprismGrand antiprismIn geometry, the grand antiprism or pentagonal double antiprismoid is a uniform polychoron bounded by 320 cells: 20 pentagonal antiprisms, and 300 tetrahedra. It is an anomalous, non-Wythoffian uniform polychoron, discovered in 1965 by Conway and Guy.- Alternate names :* Pentagonal double...
- a four dimensional polytope



