Grand antiprism - AbsoluteAstronomy.com


(Schlegel diagram wireframe)
Type	Uniform polychoron Uniform polychoron In geometry, a uniform polychoron is a polychoron or 4-polytope which is vertex-transitive and whose cells are uniform polyhedra....
Uniform index	47
Cells	100+200 (3.3.3 Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids... ) 20 (3.3.3.5 Pentagonal antiprism In geometry, the pentagonal antiprism is the third in an infinite set of antiprisms formed by an even-numbered sequence of triangle sides closed by two polygon caps. It consists of two pentagons joined to each other by a ring of 10 triangles for a total of 12 faces... )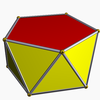
Faces	20 {5} Pentagon In geometry, a pentagon is any five-sided polygon. A pentagon may be simple or self-intersecting. The sum of the internal angles in a simple pentagon is 540°. A pentagram is an example of a self-intersecting pentagon.- Regular pentagons :In a regular pentagon, all sides are equal in length and... 700 {3} Triangle A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....
Edges	500
Vertices	100
Vertex figure Vertex figure In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...	12 (3.3.3 Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids... ) 2 (3.3.3.5 Pentagonal antiprism In geometry, the pentagonal antiprism is the third in an infinite set of antiprisms formed by an even-numbered sequence of triangle sides closed by two polygon caps. It consists of two pentagons joined to each other by a ring of 10 triangles for a total of 12 faces... )
Symmetry group Symmetry group The symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation...	Ionic diminished Coxeter group 10,2⁺,10, of order 400
Schläfli symbol	s{5}.s{5} (extended)
Properties	convex Convex polytope A convex polytope is a special case of a polytope, having the additional property that it is also a convex set of points in the n-dimensional space Rn...

In geometry

Geometry

Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....

, the grand antiprism or pentagonal double antiprismoid is a uniform polychoron

Uniform polychoron

In geometry, a uniform polychoron is a polychoron or 4-polytope which is vertex-transitive and whose cells are uniform polyhedra....

(4-dimensional uniform polytope

Polytope

In elementary geometry, a polytope is a geometric object with flat sides, which exists in any general number of dimensions. A polygon is a polytope in two dimensions, a polyhedron in three dimensions, and so on in higher dimensions...

) bounded by 320 cells

Cell (geometry)

In geometry, a cell is a three-dimensional element that is part of a higher-dimensional object.- In polytopes :A cell is a three-dimensional polyhedron element that is part of the boundary of a higher-dimensional polytope, such as a polychoron or honeycomb For example, a cubic honeycomb is made...

: 20 pentagonal antiprism

Pentagonal antiprism

In geometry, the pentagonal antiprism is the third in an infinite set of antiprisms formed by an even-numbered sequence of triangle sides closed by two polygon caps. It consists of two pentagons joined to each other by a ring of 10 triangles for a total of 12 faces...

s, and 300 tetrahedra

Tetrahedron

In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...

. It is an anomalous, non-Wythoffian uniform polychoron, discovered in 1965 by Conway

John Horton Conway

John Horton Conway is a prolific mathematician active in the theory of finite groups, knot theory, number theory, combinatorial game theory and coding theory...

and Guy.

Alternate names

Pentagonal double antiprismoid Norman W. Johnson
Gap (Jonathan Bowers: for grand antiprism)

Structure

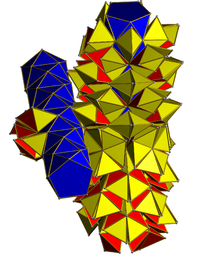
The 20 pentagonal antiprisms occur in two disjoint rings of 10 antiprisms each. The antiprisms in each ring are joined to each other via their pentagonal faces. The two rings are mutually perpendicular, in a structure similar to a duoprism

Duoprism

In geometry of 4 dimensions or higher, a duoprism is a polytope resulting from the Cartesian product of two polytopes, each of two dimensions or higher...

.

The 300 tetrahedra join the two rings to each other, and are laid out in a 2-dimensional arrangement topologically equivalent to the 2-torus and the ridge of the duocylinder.

This structure is analogous to that of the 3-dimensional antiprism

Antiprism

In geometry, an n-sided antiprism is a polyhedron composed of two parallel copies of some particular n-sided polygon, connected by an alternating band of triangles...

s. However, the grand antiprism is the only uniform analogue of the antiprism in 4 dimensions (although the 16-cell

16-cell

In four dimensional geometry, a 16-cell or hexadecachoron is a regular convex 4-polytope. It is one of the six regular convex 4-polytopes first described by the Swiss mathematician Ludwig Schläfli in the mid-19th century....

may be regarded as a regular analogue of the digonal antiprism

Tetrahedron

Vertex figure

The vertex figure of the grand antiprism is a dissected regular icosahedron: a regular icosahedron with two vertices removed. In their place 8 triangles are replaced by a pair of trapezoids, edge lengths φ, 1, 1, 1 (where φ is the golden ratio

Golden ratio

In mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989...

), joined together along their edge of length φ, to give a tetradecahedron

Tetradecahedron

A tetradecahedron is a polyhedron with 14 faces. There are numerous topologically distinct forms of a tetradecahedron, with many constructible entirely with regular polygon faces....

whose faces are the 2 trapezoid

Trapezoid

In Euclidean geometry, a convex quadrilateral with one pair of parallel sides is referred to as a trapezoid in American English and as a trapezium in English outside North America. A trapezoid with vertices ABCD is denoted...

s and the 12 remaining equilateral triangles.

12 (3.3.3 Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids... )	2 (3.3.3.5 Pentagonal antiprism In geometry, the pentagonal antiprism is the third in an infinite set of antiprisms formed by an even-numbered sequence of triangle sides closed by two polygon caps. It consists of two pentagons joined to each other by a ring of 10 triangles for a total of 12 faces... )	Dissected regular icosahedron

Construction

The grand antiprism can be constructed by diminishing the 600-cell: subtracting 20 pyramids whose bases are three-dimensional pentagonal antiprisms. Conversely, the two rings of pentagonal antiprisms in the grand antiprism may be triangulated by 10 tetrahedra joined to the triangular faces of each antiprism, and a circle of 5 tetrahedra between every pair of antiprisms, joining the 10 tetrahedra of each, yielding 150 tetrahedra per ring. These combined with the 300 tetrahedra that join the two rings together yield the 600 tetrahedra of the 600-cell.

This relationship is analogous to how a pentagonal antiprism

Pentagonal antiprism

can be constructed from an icosahedron

Icosahedron

In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids....

by removing two opposite vertices, thereby removing 5 triangles from the opposite 'poles' of the icosahedron, leaving the 10 equatorial triangles and two pentagons on the top and bottom.

Computationally speaking, this diminishing may be realized by removing two rings of vertices from the 600-cell, each ring having 10 vertices, and each lying in mutually orthogonal planes, and taking the convex hull

Convex hull

In mathematics, the convex hull or convex envelope for a set of points X in a real vector space V is the minimal convex set containing X....

of the remaining vertices.

(The snub 24-cell

Snub 24-cell

In geometry, the snub 24-cell is a convex uniform polychoron composed of 120 regular tetrahedral and 24 icosahedral cells. Five tetrahedra and three icosahedra meet at each vertex. In total it has 480 triangular faces, 432 edges, and 96 vertices....

can also be constructed by another diminishing of the 600-cell, removing 24 icosahedral pyramids. Equivalently, this may be realized as taking the convex hull of the vertices remaining after 24 vertices, corresponding to those of an inscribed 24-cell, are removed from the 600-cell.)

Projections

These are two perspective projections, projecting the polytope into a hypersphere

Hypersphere

In mathematics, an n-sphere is a generalization of the surface of an ordinary sphere to arbitrary dimension. For any natural number n, an n-sphere of radius r is defined as the set of points in -dimensional Euclidean space which are at distance r from a central point, where the radius r may be any...

, and applying a stereographic projection

Stereographic projection

The stereographic projection, in geometry, is a particular mapping that projects a sphere onto a plane. The projection is defined on the entire sphere, except at one point — the projection point. Where it is defined, the mapping is smooth and bijective. It is conformal, meaning that it...

into 3-space.

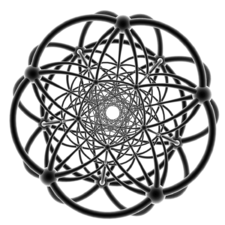Wireframe, viewed down one of the pentagonal antiprism columns.	with transparent triangular faces
Orthographic projection Orthographic projection Orthographic projection is a means of representing a three-dimensional object in two dimensions. It is a form of parallel projection, where all the projection lines are orthogonal to the projection plane, resulting in every plane of the scene appearing in affine transformation on the viewing surface... Centered on hyperplane Hyperplane A hyperplane is a concept in geometry. It is a generalization of the plane into a different number of dimensions.A hyperplane of an n-dimensional space is a flat subset with dimension n − 1... of an antiprism in one of the two rings.

External links

In the Belly of the Grand Antiprism (middle section, describing the analogy with the icosahedron and the pentagonal antiprism)