
Snub 24-cell
Encyclopedia
| Snub 24-cell | ||
 Orthogonal projection Centered on hyperplane of one icosahedron. |
||
| Type | Uniform polychoron Uniform polychoron In geometry, a uniform polychoron is a polychoron or 4-polytope which is vertex-transitive and whose cells are uniform polyhedra.... |
|
| Schläfli symbol | h0,1{3,4,3} h0,1,2{3,3,4} s{31,1,1} |
|
| Coxeter-Dynkin diagrams Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... |
||
| Cells | 144 | 96 3.3.3 Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids... (oblique)  24 3.3.3 Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...  24 3.3.3.3.3 Icosahedron In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids....  |
| Faces | 480 {3} | |
| Edges | 432 | |
| Vertices | 96 | |
| Vertex figure Vertex figure In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:... |
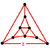 (Tridiminished icosahedron Tridiminished icosahedron In geometry, the tridiminished icosahedron is one of the Johnson solids .The 92 Johnson solids were named and described by Norman Johnson in 1966.- Related polytopes :... ) |
|
| Coxeter group Coxeter group In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example... s |
F4, [3,4,3] (half) BC4, [3,3,4] (half) D4, [31,1,1] (half) |
|
| Symmetry group Coxeter notation In geometry, Coxeter notation is a system of classifying symmetry groups, describing the angles between with fundamental reflections of a Coxeter group. It uses a bracketed notation, with modifiers to indicate certain subgroups. The notation is named after H. S. M... s |
[3+,4,3], order 576 [(3,3)+,4], order 192 [31,1,1]+, order 96 |
|
| Properties | convex Convex polytope A convex polytope is a special case of a polytope, having the additional property that it is also a convex set of points in the n-dimensional space Rn... |
|
| Uniform index | 31 32 33 | |
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, the snub 24-cell is a convex uniform polychoron
Uniform polychoron
In geometry, a uniform polychoron is a polychoron or 4-polytope which is vertex-transitive and whose cells are uniform polyhedra....
composed of 120 regular tetrahedral and 24 icosahedral cells. Five tetrahedra and three icosahedra meet at each vertex. In total it has 480 triangular faces, 432 edges, and 96 vertices.
It is one of three semiregular polychora made of two or more cells which are platonic solid
Platonic solid
In geometry, a Platonic solid is a convex polyhedron that is regular, in the sense of a regular polygon. Specifically, the faces of a Platonic solid are congruent regular polygons, with the same number of faces meeting at each vertex; thus, all its edges are congruent, as are its vertices and...
s, discovered by Thorold Gosset
Thorold Gosset
Thorold Gosset was an English lawyer and an amateur mathematician. In mathematics, he is noted for discovering and classifying the semiregular polytopes in dimensions four and higher.According to H. S. M...
in his 1900 paper. He called it a tetricosahedric for being made of tetrahedron
Tetrahedron
In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...
and icosahedron
Icosahedron
In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids....
cells. (The other two are the rectified 5-cell
Rectified 5-cell
In four dimensional geometry, the rectified 5-cell is a uniform polychoron composed of 5 regular tetrahedral and 5 regular octahedral cells. Each edge has one tetrahedron and two octahedra. Each vertex has two tetrahedra and three octahedra. In total it has 30 triangle faces, 30 edges, and 10...
and rectified 600-cell
Rectified 600-cell
In geometry, a rectified 600-cell is a uniform polychoron formed as the rectification of the regular 600-cell.There are four rectifications of the 600-cell, including the zeroth, the 600-cell itself...
.)
Alternative names
- Snub icositetrachoron
- Semi-snub polyoctahedron (John ConwayJohn Horton ConwayJohn Horton Conway is a prolific mathematician active in the theory of finite groups, knot theory, number theory, combinatorial game theory and coding theory...
) - Sadi (Jonathan Bowers: for snub disicositetrachoron)
- Tetricosahedric Thorold GossetThorold GossetThorold Gosset was an English lawyer and an amateur mathematician. In mathematics, he is noted for discovering and classifying the semiregular polytopes in dimensions four and higher.According to H. S. M...
, 1900
Geometry
The snub 24-cell is related to the truncated 24-cellTruncated 24-cell
In geometry, a truncated 5-cell is a uniform polychoron formed as the truncation of the regular 5-cell.There are two degrees of trunctions, including a bitruncation.- Truncated 5-cell:...
by an alternation operation. Half the vertices are deleted, the 24 truncated octahedron
Truncated octahedron
In geometry, the truncated octahedron is an Archimedean solid. It has 14 faces , 36 edges, and 24 vertices. Since each of its faces has point symmetry the truncated octahedron is a zonohedron....
cells become 24 icosahedron
Icosahedron
In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids....
cells, the 24 cube
Cube
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and...
s become 24 tetrahedron
Tetrahedron
In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...
cells, and the 96 deleted vertex voids create 96 new tetrahedron cells.
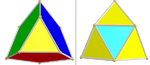
 A net of the snub 24-cell with blue icosahedra, and red and yellow tetrahedra. |
The snub 24-cell may also be constructed by a particular diminishing of the 600-cell: by removing 24 vertices from the 600-cell corresponding to those of an inscribed 24-cell, and then taking the convex hull
Convex hull
In mathematics, the convex hull or convex envelope for a set of points X in a real vector space V is the minimal convex set containing X....
of the remaining vertices. This is equivalent to removing 24 icosahedral pyramids from the 600-cell.
Conversely, the 600-cell may be constructed from the snub 24-cell by augmenting it with 24 icosahedral pyramids.
Coordinates
The vertices of a snub 24-cell centered at the origin of 4-space, with edges of length 2, are obtained by taking even permutations of(where φ = (1+√5)/2 is the golden ratio
Golden ratio
In mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989...
).
These 96 vertices can be found by partitioning each of the 96 edges of a 24-cell into the golden ratio in a consistent manner, in much the same way that the 12 vertices of an icosahedron
Icosahedron
In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids....
or "snub octahedron" can be produced by partitioning the 12 edges of an octahedron in the golden ratio. This is done by first placing vectors along the 24-cell's edges such that each two-dimensional face is bounded by a cycle, then similarly partitioning each edge into the golden ratio along the direction of its vector. The 96 vertices of the snub 24-cell, together with the 24 vertices of a 24-cell, form the 120 vertices of the 600-cell.
Structure
Each icosahedral cell is joined to 8 other icosahedral cells at 8 triangular faces in the positions corresponding to an inscribing octahedron. The remaining triangular faces are joined to tetrahedral cells, which occur in pairs that share an edge on the icosahedral cell.The tetrahedral cells may be divided into two groups, of 96 cells and 24 cells respectively. Each tetrahedral cell in the first group is joined via its triangular faces to 3 icosahedral cells and one tetrahedral cell in the second group, while each tetrahedral cell in the second group is joined to 4 tetrahedra in the first group.
Symmetry
The snub 24-cell has three vertex-transitiveVertex-transitive
In geometry, a polytope is isogonal or vertex-transitive if, loosely speaking, all its vertices are the same...
colorings based on a Wythoff construction
Wythoff construction
In geometry, a Wythoff construction, named after mathematician Willem Abraham Wythoff, is a method for constructing a uniform polyhedron or plane tiling. It is often referred to as Wythoff's kaleidoscopic construction.- Construction process :...
on a Coxeter group
Coxeter group
In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example...
from which it is alternated: F4 defines 24 interchangeable icosahedra, while the BC4 group defines two groups of icosahedra in a 8:16 counts, and finally the D4 group has 3 groups of icosahedra with 8:8:8 counts.
| Family | Constructive name | Coxeter-Dynkin diagram Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... Extended Schläfli symbol |
Vertex figure Vertex figure In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:... (Tridiminished icosahedron Tridiminished icosahedron In geometry, the tridiminished icosahedron is one of the Johnson solids .The 92 Johnson solids were named and described by Norman Johnson in 1966.- Related polytopes :... ) |
Cells Cell (geometry) In geometry, a cell is a three-dimensional element that is part of a higher-dimensional object.- In polytopes :A cell is a three-dimensional polyhedron element that is part of the boundary of a higher-dimensional polytope, such as a polychoron or honeycomb For example, a cubic honeycomb is made... (Colored as faces in vertex figures) |
|---|---|---|---|---|
| F4 [3+,4,3] o(576) |
Alternated truncated 24-cell | h0,1{3,4,3} |
 |
Three sets of 8 icosahedra (red, green, and blue) Two sets of tetrahedra: 96 (yellow) and 24 (cyan) |
| BC4 [(3,3)+,4] o(192) |
Alternated cantitruncated 16-cell | h0,1,2{3,3,4} |
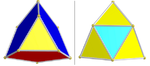 |
Two sets icosahedra: 8, 16 each (red and blue) Two sets of tetrahedra: 96 (yellow) and 24 (cyan) |
| D4 [31,1,1]+ o(96) |
Snub demitesseract | s{31,1,1} |
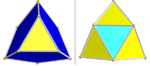 |
One set of 24 icosahedra (blue) Two sets of tetrahedra: 96 (yellow) and 24 (cyan) |
Images
| Coxeter plane | F4 | B4 |
|---|---|---|
| Graph | ||
| Dihedral symmetry | [12]+ | [8/2] |
| Coxeter plane | D4 / B3 / A2 | B2 / A3 |
| Graph | ||
| Dihedral symmetry | [6]+ | [4] |
| Perspective projections | |
|---|---|
 Perspective projection centered on an icosahedral cell, with 4D viewpoint placed at a distance of 5 times the vertex-center radius. The nearest icosahedral cell is rendered in solid color, and the other cells are in edge-outline. Cells facing away from the 4D viewpoint are culled, to reduce visual clutter. |
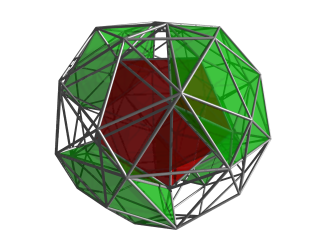 The same projection, now with 4 of the 8 icosahedral cells surrounding the central cell shown in green. |
 The same projection as above, now with the other 4 icosahedral cells surrounding the central cell shown in magenta. The animated version of this image gives a good view on the layout of these cells. From this particular viewpoint, one of the gaps containing tetrahedral cells can be seen. Each of these gaps are filled by 5 tetrahedral cells, not shown here. |
 Same projection as above, now with the central tetrahedral cell in the gap filled in. This tetrahedral cell is joined to 4 other tetrahedral cells, two of which fills the two gaps visible in this image. The other two each lies between a green tetrahedral cell, a magenta cell, and the central cell, to the left and right of the yellow tetrahedral cell. Note that in these images, cells facing away from the 4D viewpoint have been culled; hence there are only a total of 1 + 8 + 6 + 24 = 39 cells accounted for here. The other cells lie on the other side of the snub 24-cell. Part of the edge outline of one of them, an icosahedral cell, can be discerned here, overlying the yellow tetrahedron. |
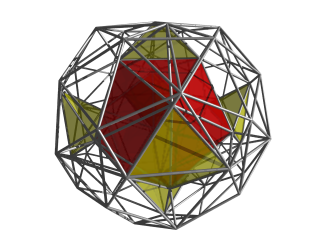 In this image, only the nearest icosahedral cell and the 6 yellow tetrahedral cells from the previous image are shown. |
 Now the 12 tetrahedral cells joined to the central icosahedral cell and the 6 yellow tetrahedral cells are shown. Each of these cells is surrounded by the central icosahedron and two of the other icosahedral cells shown earlier. |
 Finally, the other 12 tetrahedral cells joined to the 6 yellow tetrahedral cells are shown here. These cells, together with the 8 icosahedral cells shown earlier, comprise all the cells that share at least 1 vertex with the central cell. |

