
Truncated 24-cell
Encyclopedia
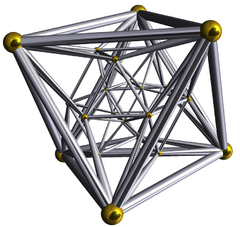 24-cell |
 Truncated 24-cell |
Bitruncated 24-cell |
|
| Schlegel diagrams centered on one [3,4] (cells at opposite at [4,3]) | |||
In geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, a truncated 5-cell is a uniform polychoron
Uniform polychoron
In geometry, a uniform polychoron is a polychoron or 4-polytope which is vertex-transitive and whose cells are uniform polyhedra....
(4-dimensional uniform polytope
Polytope
In elementary geometry, a polytope is a geometric object with flat sides, which exists in any general number of dimensions. A polygon is a polytope in two dimensions, a polyhedron in three dimensions, and so on in higher dimensions...
) formed as the truncation
Truncation (geometry)
In geometry, a truncation is an operation in any dimension that cuts polytope vertices, creating a new facet in place of each vertex.- Uniform truncation :...
of the regular 5-cell.
There are two degrees of trunctions, including a bitruncation
Bitruncation
In geometry, a bitruncation is an operation on regular polytopes. It represents a truncation beyond rectification. The original edges are lost completely and the original faces remain as smaller copies of themselves....
.
Truncated 5-cell
| Truncated 24-cell | ||
|---|---|---|
| Type | Uniform polychoron Uniform polychoron In geometry, a uniform polychoron is a polychoron or 4-polytope which is vertex-transitive and whose cells are uniform polyhedra.... |
|
| Schläfli symbol | t0,1{3,4,3} t0,1,2{3,3,4} t0,1,2,3{31,1,1} |
|
| Coxeter-Dynkin diagram Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... s |
||
| Cells | 48 | 24 4.6.6 Truncated octahedron In geometry, the truncated octahedron is an Archimedean solid. It has 14 faces , 36 edges, and 24 vertices. Since each of its faces has point symmetry the truncated octahedron is a zonohedron....  24 4.4.4 Cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and...  |
| Faces | 240 | 144 {4} Square (geometry) In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles... 96 {6} |
| Edges | 384 | |
| Vertices | 192 | |
| Vertex figure Vertex figure In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:... |
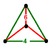   equilateral triangular pyramid |
|
| Symmetry groups Coxeter group In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example... |
F4 [3,4,3] B4 [3,3,4] D4 [31,1,1] |
|
| Properties | convex Convex polytope A convex polytope is a special case of a polytope, having the additional property that it is also a convex set of points in the n-dimensional space Rn... zonohedron Zonohedron A zonohedron is a convex polyhedron where every face is a polygon with point symmetry or, equivalently, symmetry under rotations through 180°. Any zonohedron may equivalently be described as the Minkowski sum of a set of line segments in three-dimensional space, or as the three-dimensional... |
|
| Uniform index | 23 Rectified 24-cell In geometry, the rectified 24-cell is a uniform 4-dimensional polytope , which is bounded by 48 cells: 24 cubes, and 24 cuboctahedra. It can be obtained by reducing the icositetrachoron's cells to cubes or cuboctahedra.... 24 25 Cantellated 24-cell In four-dimensional geometry, a cantellated 24-cell is a convex uniform polychoron, being a cantellation of the regular 24-cell.There are 2 unique degrees of runcinations of the 24-cell including with permutations truncations.... |
|
The truncated 24-cell is a uniform 4-dimensional polytope (or uniform polychoron
Uniform polychoron
In geometry, a uniform polychoron is a polychoron or 4-polytope which is vertex-transitive and whose cells are uniform polyhedra....
), which is bounded by 48 cells: 24 cube
Cube
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and...
s, and 24 truncated octahedra
Truncated octahedron
In geometry, the truncated octahedron is an Archimedean solid. It has 14 faces , 36 edges, and 24 vertices. Since each of its faces has point symmetry the truncated octahedron is a zonohedron....
. Each vertex contains three truncated octahedra and one cube, in an equilateral triangular pyramid vertex figure
Vertex figure
In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...
.
Construction
The truncated 24-cell can be constructed from with three symmetry groups:- F4 [3,4,3]: A truncationTruncation (geometry)In geometry, a truncation is an operation in any dimension that cuts polytope vertices, creating a new facet in place of each vertex.- Uniform truncation :...
of the 24-cell. - B4 [3,3,4]: A cantitruncation of the 16-cell16-cellIn four dimensional geometry, a 16-cell or hexadecachoron is a regular convex 4-polytope. It is one of the six regular convex 4-polytopes first described by the Swiss mathematician Ludwig Schläfli in the mid-19th century....
, with two families of truncated octahedral cells. - D4 [31,1,1]: An omnitruncation of the demitesseract, with three families of truncated octahedral cells.
It is also a zonotope: it can be formed as the Minkowski sum of the six line segments connecting opposite pairs among the twelve permutations of the vector (+1,−1,0,0).
Cartesian coordinates
The Cartesian coordinates of the vertices of a truncated 24-cell having edge length sqrt(2) are all coordinate permutations and sign combinations of:- (0,1,2,3)
The dual configuation has coordinates at all coordinate permutation and signs of
- (1,1,1,5)
- (1,3,3,3)
- (2,2,2,4)
Structure
The 24 cubical cells are joined via their square faces to the truncated octahedra; and the 24 truncated octahedra are joined to each other via their hexagonal faces.Projections
The parallel projection of the truncated 24-cell into 3-dimensional space, truncated octahedron first, has the following layout:- The projection envelope is a great rhombicuboctahedron.
- Two of the truncated octahedra project onto a truncated octahedron lying in the center of the envelope.
- Six cuboidal volumes join the square faces of this central truncated octahedron to the center of the octagonal faces of the great rhombicuboctahedron. These are the images of 12 of the cubical cells, a pair of cells to each image.
- The 12 square faces of the great rhombicuboctahedron are the images of the remaining 12 cubes.
- The 6 octagonal faces of the great rhombicuboctahedron are the images of 6 of the truncated octahedra.
- The 8 (non-uniform) truncated octahedral volumes lying between the hexagonal faces of the projection envelope and the central truncated octahedron are the images of the remaining 16 truncated octahedra, a pair of cells to each image.
Images
 Schlegel diagram (cubic Cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and... cells visible) |
 Schlegel diagram 8 of 24 truncated octahedral cells visible |
 net |
 Stereographic projection Stereographic projection The stereographic projection, in geometry, is a particular mapping that projects a sphere onto a plane. The projection is defined on the entire sphere, except at one point — the projection point. Where it is defined, the mapping is smooth and bijective. It is conformal, meaning that it... Centered on truncated tetrahedron Truncated tetrahedron In geometry, the truncated tetrahedron is an Archimedean solid. It has 4 regular hexagonal faces, 4 regular triangular faces, 12 vertices and 18 edges.- Area and volume :... |
Bitruncated 24-cell
| Bitruncated 24-cell | ||
|---|---|---|
Schlegel diagram, centered on truncated cube, with alternate cells hidden |
||
| Type | Uniform polychoron Uniform polychoron In geometry, a uniform polychoron is a polychoron or 4-polytope which is vertex-transitive and whose cells are uniform polyhedra.... |
|
| Schläfli symbol | t1,2{3,4,3} | |
| Coxeter-Dynkin diagram Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... |
||
| Cells | 48 (3.8.8) Truncated cube In geometry, the truncated cube, or truncated hexahedron, is an Archimedean solid. It has 14 regular faces , 36 edges, and 24 vertices....  |
|
| Faces | 336 | 192 {3} Triangle A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted .... 144 {8} |
| Edges | 576 | |
| Vertices | 288 | |
| Edge figure | 3.8.8 | |
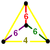
| Vertex figure Vertex figure In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:... |
 tetragonal disphenoid |
|
| Symmetry group Symmetry group The symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation... |
F4, |
|
| Properties | convex Convex polytope A convex polytope is a special case of a polytope, having the additional property that it is also a convex set of points in the n-dimensional space Rn... , isogonal, isotoxal, isochoric |
|
| Uniform index | 26 Runcinated 24-cell In four-dimensional geometry, a runcinated 24-cell is a convex uniform polychoron, being a runcination of the regular 24-cell.... 27 28 |
|
The bitruncated 24-cell is a 4-dimensional uniform polytope
Polytope
In elementary geometry, a polytope is a geometric object with flat sides, which exists in any general number of dimensions. A polygon is a polytope in two dimensions, a polyhedron in three dimensions, and so on in higher dimensions...
(or uniform polychoron
Uniform polychoron
In geometry, a uniform polychoron is a polychoron or 4-polytope which is vertex-transitive and whose cells are uniform polyhedra....
) derived from the 24-cell. It is constructed by bitruncating the 24-cell (truncating at halfway to the depth which would yield the dual 24-cell).
Being a uniform polychoron, it is vertex-transitive
Vertex-transitive
In geometry, a polytope is isogonal or vertex-transitive if, loosely speaking, all its vertices are the same...
. In addition, it is cell-transitive, consisting of 48 truncated cube
Truncated cube
In geometry, the truncated cube, or truncated hexahedron, is an Archimedean solid. It has 14 regular faces , 36 edges, and 24 vertices....
s, and also edge-transitive, with 3 truncated cube
Truncated cube
In geometry, the truncated cube, or truncated hexahedron, is an Archimedean solid. It has 14 regular faces , 36 edges, and 24 vertices....
s cells per edge and with one triangle and two octagons around each edge.
The 48 cells of the bitruncated 24-cell correspond with the 24 cells and 24 vertices of the 24-cell. As such, the centers of the 48 cells form the root system
Root system
In mathematics, a root system is a configuration of vectors in a Euclidean space satisfying certain geometrical properties. The concept is fundamental in the theory of Lie groups and Lie algebras...
of type F4.
Its vertex figure is a tetragonal disphenoid, a tetrahedron with 2 opposite edges length 1 and all 4 lateral edges length sqrt(2+sqrt(2)).
Alternative names
- Bitruncated 24-cell (Norman W. Johnson)
- 48-cell as a cell-transitive 4-polytope
- Bitruncated icositetrachoron
- Bitruncated polyoctahedron
- Tetracontaoctachoron (Cont) (Jonathan Bowers)
Structure
The truncated cubes are joined to each other via their octagonal faces in anti orientation; i. e., two adjoining truncated cubes are rotated 45 degrees relative to each other so that no two triangular faces share an edge.The sequence of truncated cubes joined to each other via opposite octagonal faces form a cycle of 8. Each truncated cube belongs to 3 such cycles. On the other hand, the sequence of truncated cubes joined to each other via opposite triangular faces form a cycle of 6. Each truncated cube belongs to 4 such cycles.
Coordinates
The Cartesian coordinates of a bitruncated 24-cell having edge length 2 are all permutations of coordinates and sign of:Projection to 3 dimensions
| Orthographic | Perspective |
|---|---|
The following animation shows the orthographic projection of the bitruncated 24-cell into 3 dimensions. The animation itself is a perspective projection from the static 3D image into 2D, with rotation added to make its structure more apparent. The images of the 48 truncated cubes are laid out as follows:
|
The following animation shows the cell-first perspective projection of the bitruncated 24-cell into 3 dimensions. Its structure is the same as the previous animation, except that there is some foreshortening due to the perspective projection. |
 |
Related regular skew polyhedron
The regular skew polyhedronRegular skew polyhedron
In geometry, the regular skew polyhedra are generalizations to the set of regular polyhedron which include the possibility of nonplanar faces or vertex figures....
, {8,4|3}, exists in 4-space with 4 octagonal around each vertex, in a zig-zagging nonplanar vertex figure. These octagonal faces can be seen on the bitruncated 24-cell, using all 576 edges and 288 vertices. The 192 triangular faces of the bitruncated 24-cell can be seen as removed. The dual regular skew polyhedron, {4,8|3}, is similarly related to the square faces of the runcinated 24-cell
Runcinated 24-cell
In four-dimensional geometry, a runcinated 24-cell is a convex uniform polychoron, being a runcination of the regular 24-cell....
.
Related polytopes
BC4:F4:

