
Cantellated 24-cell
Encyclopedia
24-cell |
Cantellated 24-cell |
Cantitruncated 24-cell |
| Orthogonal projections in F4 Coxeter plane | ||
|---|---|---|
In four-dimensional geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, a cantellated 24-cell is a convex uniform polychoron
Uniform polychoron
In geometry, a uniform polychoron is a polychoron or 4-polytope which is vertex-transitive and whose cells are uniform polyhedra....
, being a cantellation (a 2nd order truncation) of the regular 24-cell.
There are 2 unique degrees of runcinations of the 24-cell including with permutations truncations.
Cantellated 24-cell
| Cantellated 24-cell | ||
|---|---|---|
| Type | Uniform polychoron Uniform polychoron In geometry, a uniform polychoron is a polychoron or 4-polytope which is vertex-transitive and whose cells are uniform polyhedra.... |
|
| Schläfli symbol | t0,2{3,4,3} | |
| Coxeter-Dynkin diagram Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... |
||
| Cells | 144 | 24  (3.4.4.4) (3.4.4.4)24  (3.4.3.4) (3.4.3.4)Cuboctahedron In geometry, a cuboctahedron is a polyhedron with eight triangular faces and six square faces. A cuboctahedron has 12 identical vertices, with two triangles and two squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such it is a quasiregular polyhedron,... 96  (3.4.4) (3.4.4)Triangular prism In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides.... |
| Faces | 720 | 288 triangle Triangle A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted .... s 432 square Square (geometry) In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles... s |
| Edges | 864 | |
| Vertices | 288 | |
| Vertex figure Vertex figure In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:... |
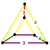 Irreg. triangular prism |
|
| Symmetry group Coxeter group In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example... |
F4, [3,4,3] | |
| Properties | convex Convex polytope A convex polytope is a special case of a polytope, having the additional property that it is also a convex set of points in the n-dimensional space Rn... |
|
| Uniform index | 24 Truncated 24-cell In geometry, a truncated 5-cell is a uniform polychoron formed as the truncation of the regular 5-cell.There are two degrees of trunctions, including a bitruncation.- Truncated 5-cell:... 25 26 Runcinated 24-cell In four-dimensional geometry, a runcinated 24-cell is a convex uniform polychoron, being a runcination of the regular 24-cell.... |
|
The cantellated 24-cell is a uniform polychoron
Uniform polychoron
In geometry, a uniform polychoron is a polychoron or 4-polytope which is vertex-transitive and whose cells are uniform polyhedra....
.
The boundary of the cantellated 24-cell is composed of
24 truncated octahedral
Truncated octahedron
In geometry, the truncated octahedron is an Archimedean solid. It has 14 faces , 36 edges, and 24 vertices. Since each of its faces has point symmetry the truncated octahedron is a zonohedron....
cells,
24 cuboctahedral
Cuboctahedron
In geometry, a cuboctahedron is a polyhedron with eight triangular faces and six square faces. A cuboctahedron has 12 identical vertices, with two triangles and two squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such it is a quasiregular polyhedron,...
cells and 96 triangular prism
Triangular prism
In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides....
s.
Together they have 288 triangular faces, 432 square faces, 864 edges, and 288 vertices.
Construction
When the cantellationCantellation (geometry)
In geometry, a cantellation is an operation in any dimension that cuts a regular polytope at its edges and vertices, creating a new facet in place of each edge and vertex. The operation also applies to regular tilings and honeycombs...
process is applied to 24-cell,
each of the 24 octahedra
Octahedron
In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....
becomes a small rhombicuboctahedron.
In addition however, since each octahedra
Octahedron
In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....
's edge was previously shared with two
other octahedra
Octahedron
In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....
, the separating edges form the three parallel edges of a
triangular prism
Triangular prism
In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides....
- 96 triangular prisms, since the 24-cell contains 96 edges.
Further, since each vertex was previously shared with 12 faces,
the vertex would split into 12 (24*12=288) new vertices.
Each group of 12 new vertices forms a cuboctahedron
Cuboctahedron
In geometry, a cuboctahedron is a polyhedron with eight triangular faces and six square faces. A cuboctahedron has 12 identical vertices, with two triangles and two squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such it is a quasiregular polyhedron,...
.
Coordinates
The Cartesian coordinates of the vertices of the cantellated 24-cell having edge length 2 are all permutations of coordinates and sign of:The permutations of the second set of coordinates coincide with the vertices of an inscribed runcitruncated tesseract.
The dual configuration has all permutations and signs of:
Structure
The 24 small rhombicuboctahedra are joined to each other via their triangular faces, to the cuboctahedraCuboctahedron
In geometry, a cuboctahedron is a polyhedron with eight triangular faces and six square faces. A cuboctahedron has 12 identical vertices, with two triangles and two squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such it is a quasiregular polyhedron,...
via their axial square faces, and to the triangular prism
Triangular prism
In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides....
s via their off-axial square faces. The cuboctahedra are joined to the triangular prisms via their triangular faces. Each triangular prism is joined to two cuboctahedra at its two ends.
Images
 Schlegel diagram |
 Showing 24 cuboctahedra Cuboctahedron In geometry, a cuboctahedron is a polyhedron with eight triangular faces and six square faces. A cuboctahedron has 12 identical vertices, with two triangles and two squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such it is a quasiregular polyhedron,... . |
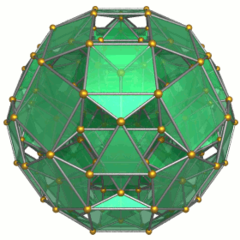 Showing 96 triangular prism Triangular prism In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides.... s. |
Cantitruncated 24-cell
| Cantitruncated 24-cell | ||
|---|---|---|
Schlegel diagram, centered on truncated cuboctahedron |
||
| Type | Uniform polychoron Uniform polychoron In geometry, a uniform polychoron is a polychoron or 4-polytope which is vertex-transitive and whose cells are uniform polyhedra.... |
|
| Schläfli symbol | t0,1,2{3,4,3} | |
| Coxeter-Dynkin diagram Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... |
||
| Cells | 144 | 24 4.6.8  96 4.4.3 Triangular prism In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides....  24 3.8.8 Truncated cube In geometry, the truncated cube, or truncated hexahedron, is an Archimedean solid. It has 14 regular faces , 36 edges, and 24 vertices....  |
| Faces | 720 | 192{3} 288{4} 96{6} 144{8} |
| Edges | 1152 | |
| Vertices | 576 | |
| Vertex figure Vertex figure In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:... |
 sphenoid Sphenoid Sphenoid may refer to:* In anatomy, the sphenoid bone* In geometry, a tetrahedron with mirror symmetry... |
|
| Symmetry group Coxeter group In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example... |
F4, [3,4,3] | |
| Properties | convex Convex polytope A convex polytope is a special case of a polytope, having the additional property that it is also a convex set of points in the n-dimensional space Rn... |
|
| Uniform index | 27 28 29 | |
The cantitruncated 24-cell is a uniform polychoron
Uniform polychoron
In geometry, a uniform polychoron is a polychoron or 4-polytope which is vertex-transitive and whose cells are uniform polyhedra....
derived from the 24-cell. It is bounded by 24 great rhombicuboctahedra corresponding with the cells of a 24-cell, 24 truncated cube
Truncated cube
In geometry, the truncated cube, or truncated hexahedron, is an Archimedean solid. It has 14 regular faces , 36 edges, and 24 vertices....
s corresponding with the cells of the dual 24-cell, and 96 triangular prism
Triangular prism
In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides....
s corresponding with the edges of the first 24-cell.
Coordinates
The Cartesian coordinates of a cantitruncated 24-cell having edge length 2 are all permutations of coordinates and sign of:- (1,1+√2,1+2√2,3+3√2)
- (0,2+√2,2+2√2,2+3√2)
The dual configuration has coordinates as all permutations and signs of:
- (1,1+√2,1+√2,5+2√2)
- (1,3+√2,3+√2,3+2√2)
- (2,2+√2,2+√2,4+2√2)
Projections
 |

