
Uniform polychoron
Encyclopedia
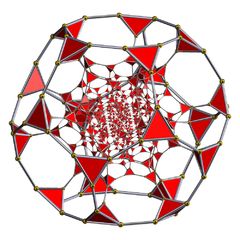
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, a uniform
Uniform polytope
A uniform polytope is a vertex-transitive polytope made from uniform polytope facets of a lower dimension. Uniform polytopes of 2 dimensions are the regular polygons....
polychoron (plural: uniform polychora) is a polychoron
Polychoron
In geometry, a polychoron or 4-polytope is a four-dimensional polytope. It is a connected and closed figure, composed of lower dimensional polytopal elements: vertices, edges, faces , and cells...
or 4-polytope
Polytope
In elementary geometry, a polytope is a geometric object with flat sides, which exists in any general number of dimensions. A polygon is a polytope in two dimensions, a polyhedron in three dimensions, and so on in higher dimensions...
which is vertex-transitive
Vertex-transitive
In geometry, a polytope is isogonal or vertex-transitive if, loosely speaking, all its vertices are the same...
and whose cells are uniform polyhedra
Uniform polyhedron
A uniform polyhedron is a polyhedron which has regular polygons as faces and is vertex-transitive...
.
This article contains the complete list of 64 non-prismatic convex uniform polychora, and describes two infinite sets of convex prismatic forms.
History of discovery
- Regular polytopeRegular polytopeIn mathematics, a regular polytope is a polytope whose symmetry is transitive on its flags, thus giving it the highest degree of symmetry. All its elements or j-faces — cells, faces and so on — are also transitive on the symmetries of the polytope, and are regular polytopes of...
s: (convex faces)- 1852: Ludwig SchläfliLudwig SchläfliLudwig Schläfli was a Swiss geometer and complex analyst who was one of the key figures in developing the notion of higher dimensional spaces. The concept of multidimensionality has since come to play a pivotal role in physics, and is a common element in science fiction...
proved in his manuscript Theorie der vielfachen Kontinuität" that there are exactly 6 regular polytopes in 4 dimensionDimensionIn physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
s and only 3 in 5 or more dimensions.
- 1852: Ludwig Schläfli
- Regular star-polychora (star polyhedronStar polyhedronIn geometry, a star polyhedron is a polyhedron which has some repetitive quality of nonconvexity giving it a star-like visual quality.There are two general kinds of star polyhedron:*Polyhedra which self-intersect in a repetitive way....
cells and/or vertex figureVertex figureIn geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...
s)- 1852: Ludwig SchläfliLudwig SchläfliLudwig Schläfli was a Swiss geometer and complex analyst who was one of the key figures in developing the notion of higher dimensional spaces. The concept of multidimensionality has since come to play a pivotal role in physics, and is a common element in science fiction...
also found 4 of the 10 regular star polychora, discounting 6 with cells or vertex figures {5/2,5} and {5,5/2}. - 1883: Edmund HessEdmund HessEdmund Hess was a German mathematician who discovered several regular polytopes.- References :* Regular Polytopes, , Dover edition, ISBN 0-486-61480-8...
completed the list of 10 of the nonconvex regular polychora, in his book (in German) Einleitung in die Lehre von der Kugelteilung mit besonderer Berücksichtigung ihrer Anwendung auf die Theorie der Gleichflächigen und der gleicheckigen Polyeder http://www.hti.umich.edu/cgi/b/bib/bibperm?q1=ABN8623.0001.001.
- 1852: Ludwig Schläfli
- Convex semiregular polytopes: (Various definitions before Coxeter's uniform category)
- 1900: Thorold GossetThorold GossetThorold Gosset was an English lawyer and an amateur mathematician. In mathematics, he is noted for discovering and classifying the semiregular polytopes in dimensions four and higher.According to H. S. M...
enumerated the list of nonprismatic semiregular convex polytopes with regular cells (Platonic solidPlatonic solidIn geometry, a Platonic solid is a convex polyhedron that is regular, in the sense of a regular polygon. Specifically, the faces of a Platonic solid are congruent regular polygons, with the same number of faces meeting at each vertex; thus, all its edges are congruent, as are its vertices and...
s) in his publication On the Regular and Semi-Regular Figures in Space of n Dimensions. - 1910: Alicia Boole StottAlicia Boole StottAlicia Boole Stott was the third daughter of George Boole and Mary Everest Boole, born in Cork, Ireland. Before marrying Walter Stott, an actuary, in 1890, she was known as Alicia Boole...
, in her publication Geometrical deduction of semiregular from regular polytopes and space fillings, expanded the definition by also allowing Archimedean solidArchimedean solidIn geometry an Archimedean solid is a highly symmetric, semi-regular convex polyhedron composed of two or more types of regular polygons meeting in identical vertices...
and prismPrism (geometry)In geometry, a prism is a polyhedron with an n-sided polygonal base, a translated copy , and n other faces joining corresponding sides of the two bases. All cross-sections parallel to the base faces are the same. Prisms are named for their base, so a prism with a pentagonal base is called a...
cells. This construction enumerated 45 semiregular polychora. - 1911: Pieter Hendrik SchoutePieter Hendrik SchoutePieter Hendrik Schoute was a Dutch mathematician known for his work on regular polytopes and Euclidean geometry.- References :...
published Analytic treatment of the polytopes regularly derived from the regular polytopes, followed Boole-Stott's notations, enumerating the convex uniform polytopes by symmetry based on 5-cell, 8-cell/16-cell16-cellIn four dimensional geometry, a 16-cell or hexadecachoron is a regular convex 4-polytope. It is one of the six regular convex 4-polytopes first described by the Swiss mathematician Ludwig Schläfli in the mid-19th century....
, and 24-cell. - 1912: E. L. ElteE. L. ElteEmanuel Lodewijk Elte was a Dutch mathematician. He is noted for discovering and classifying semiregular polytopes in dimensions four and higher....
independently expanded on Gosset's list with the publication The Semiregular Polytopes of the Hyperspaces, polytopes with one or two types of semiregular facets.
- 1900: Thorold Gosset
- Convex uniform polytopes:
- 1940: The search was expanded systematically by H.S.M. CoxeterHarold Scott MacDonald CoxeterHarold Scott MacDonald "Donald" Coxeter, was a British-born Canadian geometer. Coxeter is regarded as one of the great geometers of the 20th century. He was born in London but spent most of his life in Canada....
in his publication Regular and Semi-Regular Polytopes. - Convex uniform polychora:
- 1965: The complete list of convex forms was finally done by John Horton ConwayJohn Horton ConwayJohn Horton Conway is a prolific mathematician active in the theory of finite groups, knot theory, number theory, combinatorial game theory and coding theory...
and Michael Guy, in their publication Four-Dimensional Archimedean Polytopes, established by computer analysis, adding only one non-Wythoffian convex polychoron, the grand antiprismGrand antiprismIn geometry, the grand antiprism or pentagonal double antiprismoid is a uniform polychoron bounded by 320 cells: 20 pentagonal antiprisms, and 300 tetrahedra. It is an anomalous, non-Wythoffian uniform polychoron, discovered in 1965 by Conway and Guy.- Alternate names :* Pentagonal double...
. - 1966 N.W. Johnson completes his Ph.D. dissertation The Theory of Uniform Polytopes and Honeycombs under advisor Coxeter, completes the basic theory of uniform polytopes for dimensions 4 and higher
- 1997: A complete enumeration of the names and elements of the convex uniform polychora is given online by George OlshevskyGeorge OlshevskyGeorge Olshevsky is a freelance editor, writer, publisher, amateur paleontologist, and mathematician living in San Diego, California.Olshevsky maintains the comprehensive online Dinosaur Genera List...
. - 2004: A proof that the Conway-Guy set is complete was published by Marco Möller in his dissertation, Vierdimensionale Archimedische Polytope.
- 1965: The complete list of convex forms was finally done by John Horton Conway
- 1940: The search was expanded systematically by H.S.M. Coxeter
- Nonregular uniform star polychora: (similar to the nonconvex uniform polyhedra)
- Ongoing: Thousands of nonconvex uniform polychora are known, but mostly unpublished. The list is presumed not to be complete, and there is no estimate of how long the complete list will be. Participating researchers include Jonathan Bowers, George OlshevskyGeorge OlshevskyGeorge Olshevsky is a freelance editor, writer, publisher, amateur paleontologist, and mathematician living in San Diego, California.Olshevsky maintains the comprehensive online Dinosaur Genera List...
and Norman Johnson.
- Ongoing: Thousands of nonconvex uniform polychora are known, but mostly unpublished. The list is presumed not to be complete, and there is no estimate of how long the complete list will be. Participating researchers include Jonathan Bowers, George Olshevsky
Regular polychora
The uniform polychora include two special subsets, which satisfy additional requirements:- The 16 regular polychora, with the property that all cells, faces, edges, and vertices are congruent:
- 6 convex regular 4-polytopeConvex regular 4-polytopeIn mathematics, a convex regular 4-polytope is a 4-dimensional polytope that is both regular and convex. These are the four-dimensional analogs of the Platonic solids and the regular polygons ....
s; - 10 Schläfli-Hess polychora.
- 6 convex regular 4-polytope
Convex uniform polychora
There are 64 convex uniform polychora, including the 6 regular convex polychora, and excluding the infinite sets of the duoprismDuoprism
In geometry of 4 dimensions or higher, a duoprism is a polytope resulting from the Cartesian product of two polytopes, each of two dimensions or higher...
s and the antiprismatic hyperprisms.
- 5 are polyhedral prisms based on the Platonic solidPlatonic solidIn geometry, a Platonic solid is a convex polyhedron that is regular, in the sense of a regular polygon. Specifically, the faces of a Platonic solid are congruent regular polygons, with the same number of faces meeting at each vertex; thus, all its edges are congruent, as are its vertices and...
s (1 overlap with regular since a cubic hyperprism is a tesseractTesseractIn geometry, the tesseract, also called an 8-cell or regular octachoron or cubic prism, is the four-dimensional analog of the cube. The tesseract is to the cube as the cube is to the square. Just as the surface of the cube consists of 6 square faces, the hypersurface of the tesseract consists of 8...
) - 13 are polyhedral prisms based on the Archimedean solidArchimedean solidIn geometry an Archimedean solid is a highly symmetric, semi-regular convex polyhedron composed of two or more types of regular polygons meeting in identical vertices...
s - 9 are in the self-dual regular A4 [3,3,3] group (5-cell) family.
- 9 are in the self-dual regular F4 [3,4,3] group (24-cell) family. (Excluding snub 24-cell)
- 15 are in the regular B4 [3,3,4] group (tesseractTesseractIn geometry, the tesseract, also called an 8-cell or regular octachoron or cubic prism, is the four-dimensional analog of the cube. The tesseract is to the cube as the cube is to the square. Just as the surface of the cube consists of 6 square faces, the hypersurface of the tesseract consists of 8...
/16-cell16-cellIn four dimensional geometry, a 16-cell or hexadecachoron is a regular convex 4-polytope. It is one of the six regular convex 4-polytopes first described by the Swiss mathematician Ludwig Schläfli in the mid-19th century....
) family (3 overlap with 24-cell family) - 15 are in the regular H4 [3,3,5] group (120-cell/600-cell) family.
- 1 special snub form in the [3,4,3] group (24-cell) family.
- 1 special non-Wythoffian polychoron, the grand antiprism.
- TOTAL: 68 − 4 = 64
These 64 uniform polychora are indexed below by George Olshevsky
George Olshevsky
George Olshevsky is a freelance editor, writer, publisher, amateur paleontologist, and mathematician living in San Diego, California.Olshevsky maintains the comprehensive online Dinosaur Genera List...
. Repeated symmetry forms are indexed in brackets.
In addition to the 64 above, there are 2 infinite prismatic sets that generate all of the remaining convex forms:
- Set of uniform antiprismatic prisms - s{p,2}x{} - Polyhedral prisms of two antiprisms.
- Set of uniform duoprismDuoprismIn geometry of 4 dimensions or higher, a duoprism is a polytope resulting from the Cartesian product of two polytopes, each of two dimensions or higher...
s - {p}x{q} - A product of two polygons.
The A4 family
The 5-cell has diploid pentachoric [3,3,3] symmetry, of order 120, isomorphic to the permutations of five elements, because all pairs of vertices are related in the same way. The three forms marked with an asteriskAsterisk
An asterisk is a typographical symbol or glyph. It is so called because it resembles a conventional image of a star. Computer scientists and mathematicians often pronounce it as star...
,*, have the higher extended pentachoric symmetry, of order 240,
Facets (cells) are given, grouped in their Coxeter-Dynkin locations by removing specified nodes.
| # | Johnson Name Bowers name (and acronym) |
Vertex figure Vertex figure In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:... |
Coxeter-Dynkin Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... and Schläfli symbols |
Cell counts by location | Element counts | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
(5) |
(10) |
(10) |
(5) |
Cells | Faces | Edges | Vertices | ||||
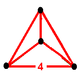
| 1 | 5-cell Pentachoron (pen) |
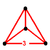 |
{3,3,3} |
(4) (3.3.3) Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids... |
5 | 10 | 10 | 5 | |||
| 2 | rectified 5-cell Rectified 5-cell In four dimensional geometry, the rectified 5-cell is a uniform polychoron composed of 5 regular tetrahedral and 5 regular octahedral cells. Each edge has one tetrahedron and two octahedra. Each vertex has two tetrahedra and three octahedra. In total it has 30 triangle faces, 30 edges, and 10... Rectified pentachoron (rap) |
 |
t1{3,3,3} |
(3) (3.3.3.3) Octahedron In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex.... |
(2) (3.3.3) Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids... |
10 | 30 | 30 | 10 | ||
| 3 | truncated 5-cell Truncated 5-cell In geometry, a truncated 5-cell is a uniform polychoron formed as the truncation of the regular 5-cell.There are two degrees of trunctions, including a bitruncation.- Truncated 5-cell:... Truncated pentachoron (tip) |
 |
t0,1{3,3,3} |
(3) (3.6.6) Truncated tetrahedron In geometry, the truncated tetrahedron is an Archimedean solid. It has 4 regular hexagonal faces, 4 regular triangular faces, 12 vertices and 18 edges.- Area and volume :... |
(1) (3.3.3) Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids... |
10 | 30 | 40 | 20 | ||
| 4 | cantellated 5-cell Cantellated 5-cell In four-dimensional geometry, a cantellated 5-cell is a convex uniform polychoron, being a cantellation of the regular 5-cell.There are 2 unique degrees of runcinations of the 5-cell including with permutations truncations.... Small rhombated pentachoron (srip) |
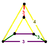 |
t0,2{3,3,3} |
(2) (3.4.3.4) Cuboctahedron In geometry, a cuboctahedron is a polyhedron with eight triangular faces and six square faces. A cuboctahedron has 12 identical vertices, with two triangles and two squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such it is a quasiregular polyhedron,... |
(2) (3.4.4) Triangular prism In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides.... |
(1) (3.3.3.3) Octahedron In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex.... |
20 | 80 | 90 | 30 | |
| 5 | *runcinated 5-cell Small prismated decachoron (spid) |
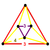 |
t0,3{3,3,3} |
(1) (3.3.3) Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids... |
(3) (3.4.4) Triangular prism In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides.... |
(3) (3.4.4) Triangular prism In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides.... |
(1) (3.3.3) Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids... |
30 | 70 | 60 | 20 |
| 6 | *bitruncated 5-cell Decachoron (deca) |
 |
t1,2{3,3,3} |
(2) (3.6.6) Truncated tetrahedron In geometry, the truncated tetrahedron is an Archimedean solid. It has 4 regular hexagonal faces, 4 regular triangular faces, 12 vertices and 18 edges.- Area and volume :... |
(2) (3.6.6) Truncated tetrahedron In geometry, the truncated tetrahedron is an Archimedean solid. It has 4 regular hexagonal faces, 4 regular triangular faces, 12 vertices and 18 edges.- Area and volume :... |
10 | 40 | 60 | 30 | ||
| 7 | cantitruncated 5-cell Great rhombated pentachoron (grip) |
 |
t0,1,2{3,3,3} |
(2) (4.6.6) Truncated octahedron In geometry, the truncated octahedron is an Archimedean solid. It has 14 faces , 36 edges, and 24 vertices. Since each of its faces has point symmetry the truncated octahedron is a zonohedron.... |
(1) (3.4.4) Triangular prism In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides.... |
(1) (3.6.6) Truncated tetrahedron In geometry, the truncated tetrahedron is an Archimedean solid. It has 4 regular hexagonal faces, 4 regular triangular faces, 12 vertices and 18 edges.- Area and volume :... |
20 | 80 | 120 | 60 | |
| 8 | runcitruncated 5-cell Prismatotrhombated pentachoron (prip) |
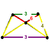 |
t0,1,3{3,3,3} |
(1) (3.6.6) Truncated tetrahedron In geometry, the truncated tetrahedron is an Archimedean solid. It has 4 regular hexagonal faces, 4 regular triangular faces, 12 vertices and 18 edges.- Area and volume :... |
(2) (4.4.6) Hexagonal prism In geometry, the hexagonal prism is a prism with hexagonal base. The shape has 8 faces, 18 edges, and 12 vertices.Since it has eight faces, it is an octahedron. However, the term octahedron is primarily used to refer to the regular octahedron, which has eight triangular faces... |
(1) (3.4.4) Triangular prism In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides.... |
(1) (3.4.3.4) Cuboctahedron In geometry, a cuboctahedron is a polyhedron with eight triangular faces and six square faces. A cuboctahedron has 12 identical vertices, with two triangles and two squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such it is a quasiregular polyhedron,... |
30 | 120 | 150 | 60 |
| 9 | *omnitruncated 5-cell Great prismated decachoron (gippid) |
 |
t0,1,2,3{3,3,3} |
(1) (4.6.6) Truncated octahedron In geometry, the truncated octahedron is an Archimedean solid. It has 14 faces , 36 edges, and 24 vertices. Since each of its faces has point symmetry the truncated octahedron is a zonohedron.... |
(1) (4.4.6) Hexagonal prism In geometry, the hexagonal prism is a prism with hexagonal base. The shape has 8 faces, 18 edges, and 12 vertices.Since it has eight faces, it is an octahedron. However, the term octahedron is primarily used to refer to the regular octahedron, which has eight triangular faces... |
(1) (4.4.6) Hexagonal prism In geometry, the hexagonal prism is a prism with hexagonal base. The shape has 8 faces, 18 edges, and 12 vertices.Since it has eight faces, it is an octahedron. However, the term octahedron is primarily used to refer to the regular octahedron, which has eight triangular faces... |
(1) (4.6.6) Truncated octahedron In geometry, the truncated octahedron is an Archimedean solid. It has 14 faces , 36 edges, and 24 vertices. Since each of its faces has point symmetry the truncated octahedron is a zonohedron.... |
30 | 150 | 240 | 120 |
Graphs
Three Coxeter plane 2D projectionsOrthographic projection
Orthographic projection is a means of representing a three-dimensional object in two dimensions. It is a form of parallel projection, where all the projection lines are orthogonal to the projection plane, resulting in every plane of the scene appearing in affine transformation on the viewing surface...
are given, for the A4, A3, A2 Coxeter group
Coxeter group
In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example...
s, showing symmetry order 5,4,3, and doubled on even Ak orders to 10,4,6 for symmetric Coxeter diagrams.
The 3D picture are drawn as Schlegel diagram projections, centered on the cell at pos. 3, with a consistent orientation, and the 5 cells at position 0 are shown solid.
| # | Johnson Name Bowers name (and acronym) |
Coxeter-Dynkin Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... and Schläfli symbols |
Coxeter plane graphs | Schlegel diagram |
|||
|---|---|---|---|---|---|---|---|
| A4 [5] |
A3 [4] |
A2 [3] |
Tetrahedron centered |
Dual tetrahedron centered |
|||
| 1 | 5-cell Pentachoron (pen) |
{3,3,3} |
 |
||||
| 2 | rectified 5-cell Rectified 5-cell In four dimensional geometry, the rectified 5-cell is a uniform polychoron composed of 5 regular tetrahedral and 5 regular octahedral cells. Each edge has one tetrahedron and two octahedra. Each vertex has two tetrahedra and three octahedra. In total it has 30 triangle faces, 30 edges, and 10... Rectified pentachoron (rap) |
t1{3,3,3} |
 |
||||
| 3 | truncated 5-cell Truncated 5-cell In geometry, a truncated 5-cell is a uniform polychoron formed as the truncation of the regular 5-cell.There are two degrees of trunctions, including a bitruncation.- Truncated 5-cell:... Truncated pentachoron (tip) |
t0,1{3,3,3} |
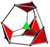 |
||||
| 4 | cantellated 5-cell Cantellated 5-cell In four-dimensional geometry, a cantellated 5-cell is a convex uniform polychoron, being a cantellation of the regular 5-cell.There are 2 unique degrees of runcinations of the 5-cell including with permutations truncations.... Small rhombated pentachoron (srip) |
t0,2{3,3,3} |
 |
||||
| 5 | *runcinated 5-cell Small prismated dodecachoron (spid) |
t0,3{3,3,3} |
 |
||||
| 6 | *bitruncated 5-cell Decachoron (deca) |
t1,2{3,3,3} |
 |
||||
| 7 | cantitruncated 5-cell Great rhombated pentachoron (grip) |
t0,1,2{3,3,3} |
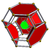 |
||||
| 8 | runcitruncated 5-cell Prismatotrhombated pentachoron (prip) |
t0,1,3{3,3,3} |
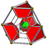 |
||||
| 9 | *omnitruncated 5-cell Great prismated decachoron (gippid) |
t0,1,2,3{3,3,3} |
 |
||||
Coordinates
The coordinates of uniform 4-polytopes with pentachoric symmetry can be generated as permutations of simple integers in 5-space, all in hyperplanes with normal vector (1,1,1,1,1). The A4 Coxeter groupCoxeter group
In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example...
is palindromic
Palindrome
A palindrome is a word, phrase, number, or other sequence of units that can be read the same way in either direction, with general allowances for adjustments to punctuation and word dividers....
, so repeated polytopes exist in pairs of dual configurations. There are 3 symmetric positions, and 6 pairs making the total 15 permutations of one or more rings. All 15 are listed here in order of binary arithmetic for clarity of the coordinate generation from the rings in each corresponding Coxeter-Dynkin diagram.
The number of vertices can be deduced here from the permutation
Permutation
In mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
s of the number of coordinates, peaking at 5 factorial
Factorial
In mathematics, the factorial of a non-negative integer n, denoted by n!, is the product of all positive integers less than or equal to n...
for the omnitruncated form with 5 unique coordinate values.
| # | Base point | Name (symmetric name) |
Coxeter-Dynkin Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... |
Vertices |
|---|---|---|---|---|
| 1 | (0, 0, 0, 0, 1) | 5-cell | 5 | |
| 2 | (0, 0, 0, 1, 1) | Rectified 5-cell Rectified 5-cell In four dimensional geometry, the rectified 5-cell is a uniform polychoron composed of 5 regular tetrahedral and 5 regular octahedral cells. Each edge has one tetrahedron and two octahedra. Each vertex has two tetrahedra and three octahedra. In total it has 30 triangle faces, 30 edges, and 10... |
10 | |
| 3 | (0, 0, 0, 1, 2) | Truncated 5-cell Truncated 5-cell In geometry, a truncated 5-cell is a uniform polychoron formed as the truncation of the regular 5-cell.There are two degrees of trunctions, including a bitruncation.- Truncated 5-cell:... |
20 | |
| 4 | (0, 0, 1, 1, 1) | Birectified 5-cell (rectified 5-cell Rectified 5-cell In four dimensional geometry, the rectified 5-cell is a uniform polychoron composed of 5 regular tetrahedral and 5 regular octahedral cells. Each edge has one tetrahedron and two octahedra. Each vertex has two tetrahedra and three octahedra. In total it has 30 triangle faces, 30 edges, and 10... ) |
10 | |
| 5 | (0, 0, 1, 1, 2) | Cantellated 5-cell Cantellated 5-cell In four-dimensional geometry, a cantellated 5-cell is a convex uniform polychoron, being a cantellation of the regular 5-cell.There are 2 unique degrees of runcinations of the 5-cell including with permutations truncations.... |
30 | |
| 6 | (0, 0, 1, 2, 2) | Bitruncated 5-cell | 30 | |
| 7 | (0, 0, 1, 2, 3) | Cantitruncated 5-cell | 60 | |
| 8 | (0, 1, 1, 1, 1) | Trirectified 5-cell (5-cell) |
5 | |
| 9 | (0, 1, 1, 1, 2) | Runcinated 5-cell | 20 | |
| 10 | (0, 1, 1, 2, 2) | Bicantellated 5-cell (cantellated 5-cell Cantellated 5-cell In four-dimensional geometry, a cantellated 5-cell is a convex uniform polychoron, being a cantellation of the regular 5-cell.There are 2 unique degrees of runcinations of the 5-cell including with permutations truncations.... ) |
30 | |
| 11 | (0, 1, 1, 2, 3) | Runcitruncated 5-cell | 60 | |
| 12 | (0, 1, 2, 2, 2) | Tritruncated 5-cell (truncated 5-cell Truncated 5-cell In geometry, a truncated 5-cell is a uniform polychoron formed as the truncation of the regular 5-cell.There are two degrees of trunctions, including a bitruncation.- Truncated 5-cell:... ) |
20 | |
| 13 | (0, 1, 2, 2, 3) | Runcicantellated 5-cell (runcitruncated 5-cell) |
60 | |
| 14 | (0, 1, 2, 3, 3) | Bicantitruncated 5-cell (cantitruncated 5-cell) |
60 | |
| 15 | (0, 1, 2, 3, 4) | Omnitruncated 5-cell | 120 |
The BC4 family
This family has diploid hexadecachoric symmetry, of order 24*16=384: 4!=24 permutations of the four axes, 24=16 for reflection in each axis.Tesseract truncations
| # | Johnson Name (Bowers style acronym) |
Vertex figure Vertex figure In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:... |
Coxeter-Dynkin Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... and Schläfli symbols |
Cell counts by location | Element counts | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
(8) |
(24) |
(32) |
(16) |
Cells | Faces | Edges | Vertices | ||||
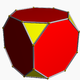
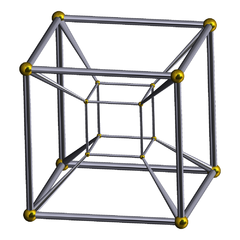
| 10 | 8-cell or tesseract Tesseract In geometry, the tesseract, also called an 8-cell or regular octachoron or cubic prism, is the four-dimensional analog of the cube. The tesseract is to the cube as the cube is to the square. Just as the surface of the cube consists of 6 square faces, the hypersurface of the tesseract consists of 8... (tes) |
 |
{4,3,3} |
(4) (4.4.4) Cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and... |
8 | 24 | 32 | 16 | |||
| 11 | rectified 8-cell Rectified tesseract In geometry, the rectified tesseract, or rectified 8-cell is a uniform polychoron bounded by 24 cells: 8 cuboctahedra, and 16 tetrahedra.... (rit) |
 |
t1{4,3,3} |
(3) (3.4.3.4) Cuboctahedron In geometry, a cuboctahedron is a polyhedron with eight triangular faces and six square faces. A cuboctahedron has 12 identical vertices, with two triangles and two squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such it is a quasiregular polyhedron,... |
(2) (3.3.3) Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids... |
24 | 88 | 96 | 32 | ||
| 13 | truncated 8-cell Truncated tesseract In geometry, a truncated tesseract is a uniform polychoron formed as the truncation of the regular tesseract.There are three trunctions, including a bitruncation, and a tritruncation, which creates the truncated 16-cell.... (tat) |
 |
t0,1{4,3,3} |
(3) (3.8.8) Truncated cube In geometry, the truncated cube, or truncated hexahedron, is an Archimedean solid. It has 14 regular faces , 36 edges, and 24 vertices.... |
(1) (3.3.3) Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids... |
24 | 88 | 128 | 64 | ||
| 14 | cantellated 8-cell Cantellated tesseract In four-dimensional geometry, a cantellated tesseract is a convex uniform polychoron, being a cantellation of the regular tesseract.There are four degrees of cantellations of the tesseract including with permutations truncations... (srit) |
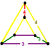 |
t0,2{4,3,3} |
(1) (3.4.4.4) |
(2) (3.4.4) Triangular prism In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides.... |
(1) (3.3.3.3) Octahedron In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex.... |
56 | 248 | 288 | 96 | |
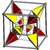
| 15 | runcinated 8-cell Runcinated tesseract In four-dimensional geometry, a runcinated tesseract is a convex uniform polychoron, being a runcination of the regular tesseract.... (also runcinated 16-cell) (sidpith) |
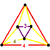 |
t0,3{4,3,3} |
(1) (4.4.4) Cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and... |
(3) (4.4.4) Cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and... |
(3) (3.4.4) Triangular prism In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides.... |
(1) (3.3.3) Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids... |
80 | 208 | 192 | 64 |
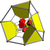
| 16 | bitruncated 8-cell (also bitruncated 16-cell) (tah) |
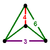 |
t1,2{4,3,3} |
(2) (4.6.6) Truncated octahedron In geometry, the truncated octahedron is an Archimedean solid. It has 14 faces , 36 edges, and 24 vertices. Since each of its faces has point symmetry the truncated octahedron is a zonohedron.... |
(2) (3.6.6) Truncated tetrahedron In geometry, the truncated tetrahedron is an Archimedean solid. It has 4 regular hexagonal faces, 4 regular triangular faces, 12 vertices and 18 edges.- Area and volume :... |
24 | 120 | 192 | 96 | ||
| 18 | cantitruncated 8-cell (grit) | 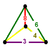 |
t0,1,2{4,3,3} |
(2)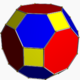 (4.6.8) Truncated cuboctahedron In geometry, the truncated cuboctahedron is an Archimedean solid. It has 12 square faces, 8 regular hexagonal faces, 6 regular octagonal faces, 48 vertices and 72 edges... |
(1) (3.4.4) Triangular prism In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides.... |
(1) (3.6.6) Truncated tetrahedron In geometry, the truncated tetrahedron is an Archimedean solid. It has 4 regular hexagonal faces, 4 regular triangular faces, 12 vertices and 18 edges.- Area and volume :... |
56 | 248 | 384 | 192 | |
| 19 | runcitruncated 8-cell (proh) |  |
t0,1,3{4,3,3} |
(1) (3.8.8) Truncated cube In geometry, the truncated cube, or truncated hexahedron, is an Archimedean solid. It has 14 regular faces , 36 edges, and 24 vertices.... |
(2) (4.4.8) Octagonal prism In geometry, the octagonal prism is the sixth in an infinite set of prisms, formed by square sides and two regular octagon caps.If faces are all regular, it is a semiregular polyhedron.- Use :... |
(1) (3.4.4) Triangular prism In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides.... |
(1) (3.4.3.4) Cuboctahedron In geometry, a cuboctahedron is a polyhedron with eight triangular faces and six square faces. A cuboctahedron has 12 identical vertices, with two triangles and two squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such it is a quasiregular polyhedron,... |
80 | 368 | 480 | 192 |
| 21 | omnitruncated 8-cell (also omnitruncated 16-cell) (gidpith) |
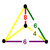 |
t0,1,2,3{3,3,4} |
(1) (4.6.8) Truncated cuboctahedron In geometry, the truncated cuboctahedron is an Archimedean solid. It has 12 square faces, 8 regular hexagonal faces, 6 regular octagonal faces, 48 vertices and 72 edges... |
(1) (4.4.8) Octagonal prism In geometry, the octagonal prism is the sixth in an infinite set of prisms, formed by square sides and two regular octagon caps.If faces are all regular, it is a semiregular polyhedron.- Use :... |
(1) (4.4.6) Hexagonal prism In geometry, the hexagonal prism is a prism with hexagonal base. The shape has 8 faces, 18 edges, and 12 vertices.Since it has eight faces, it is an octahedron. However, the term octahedron is primarily used to refer to the regular octahedron, which has eight triangular faces... |
(1) (4.6.6) Truncated octahedron In geometry, the truncated octahedron is an Archimedean solid. It has 14 faces , 36 edges, and 24 vertices. Since each of its faces has point symmetry the truncated octahedron is a zonohedron.... |
80 | 464 | 768 | 384 |
16-cell truncations
| # | Johnson Name (Bowers style acronym) | Vertex figure Vertex figure In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:... |
Coxeter-Dynkin Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... and Schläfli symbols |
Cell counts by location | Element counts | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
(8) |
(24) |
(32) |
(16) |
Cells | Faces | Edges | Vertices | ||||
| 12 | 16-cell 16-cell In four dimensional geometry, a 16-cell or hexadecachoron is a regular convex 4-polytope. It is one of the six regular convex 4-polytopes first described by the Swiss mathematician Ludwig Schläfli in the mid-19th century.... (hex) |
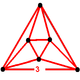 |
{3,3,4} |
(8) (3.3.3) Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids... |
16 | 32 | 24 | 8 | |||
| [22] | *rectified 16-cell (Same as 24-cell) (ico) |
 |
t1{3,3,4} |
(2) (3.3.3.3) Octahedron In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex.... |
(4) (3.3.3.3) Octahedron In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex.... |
24 | 96 | 96 | 24 | ||
| 17 | truncated 16-cell (thex) | 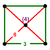 |
t0,1{3,3,4} |
(1) (3.3.3.3) Octahedron In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex.... |
(4) (3.6.6) Truncated tetrahedron In geometry, the truncated tetrahedron is an Archimedean solid. It has 4 regular hexagonal faces, 4 regular triangular faces, 12 vertices and 18 edges.- Area and volume :... |
24 | 96 | 120 | 48 | ||
| [23] | *cantellated 16-cell (Same as rectified 24-cell Rectified 24-cell In geometry, the rectified 24-cell is a uniform 4-dimensional polytope , which is bounded by 48 cells: 24 cubes, and 24 cuboctahedra. It can be obtained by reducing the icositetrachoron's cells to cubes or cuboctahedra.... ) (rico) |
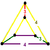 |
t0,2{3,3,4} |
(1) (3.4.3.4) Cuboctahedron In geometry, a cuboctahedron is a polyhedron with eight triangular faces and six square faces. A cuboctahedron has 12 identical vertices, with two triangles and two squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such it is a quasiregular polyhedron,... |
(2) (4.4.4) Cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and... |
(2) (3.4.3.4) Cuboctahedron In geometry, a cuboctahedron is a polyhedron with eight triangular faces and six square faces. A cuboctahedron has 12 identical vertices, with two triangles and two squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such it is a quasiregular polyhedron,... |
48 | 240 | 288 | 96 | |
| [15] | runcinated 16-cell Runcinated tesseract In four-dimensional geometry, a runcinated tesseract is a convex uniform polychoron, being a runcination of the regular tesseract.... (also runcinated 8-cell) (sidpith) |
 |
t0,3{3,3,4} |
(1) (4.4.4) Cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and... |
(3) (4.4.4) Cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and... |
(3) (3.4.4) Triangular prism In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides.... |
(1) (3.3.3) Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids... |
80 | 208 | 192 | 64 |
| [16] | bitruncated 16-cell (also bitruncated 8-cell) (tah) |
 |
t1,2{3,3,4} |
(2) (4.6.6) Truncated octahedron In geometry, the truncated octahedron is an Archimedean solid. It has 14 faces , 36 edges, and 24 vertices. Since each of its faces has point symmetry the truncated octahedron is a zonohedron.... |
(2) (3.6.6) Truncated tetrahedron In geometry, the truncated tetrahedron is an Archimedean solid. It has 4 regular hexagonal faces, 4 regular triangular faces, 12 vertices and 18 edges.- Area and volume :... |
24 | 120 | 192 | 96 | ||
| [24] | *cantitruncated 16-cell (Same as truncated 24-cell Truncated 24-cell In geometry, a truncated 5-cell is a uniform polychoron formed as the truncation of the regular 5-cell.There are two degrees of trunctions, including a bitruncation.- Truncated 5-cell:... ) (tico) |
 |
t0,1,2{3,3,4} |
(1) (4.6.6) Truncated octahedron In geometry, the truncated octahedron is an Archimedean solid. It has 14 faces , 36 edges, and 24 vertices. Since each of its faces has point symmetry the truncated octahedron is a zonohedron.... |
(1) (4.4.4) Cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and... |
(2) (4.6.6) Truncated octahedron In geometry, the truncated octahedron is an Archimedean solid. It has 14 faces , 36 edges, and 24 vertices. Since each of its faces has point symmetry the truncated octahedron is a zonohedron.... |
48 | 240 | 384 | 192 | |
| 20 | runcitruncated 16-cell (prit) | 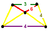 |
t0,1,3{3,3,4} |
(1) (3.4.4.4) |
(1) (4.4.4) Cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and... |
(2) (4.4.6) Hexagonal prism In geometry, the hexagonal prism is a prism with hexagonal base. The shape has 8 faces, 18 edges, and 12 vertices.Since it has eight faces, it is an octahedron. However, the term octahedron is primarily used to refer to the regular octahedron, which has eight triangular faces... |
(1) (3.6.6) Truncated tetrahedron In geometry, the truncated tetrahedron is an Archimedean solid. It has 4 regular hexagonal faces, 4 regular triangular faces, 12 vertices and 18 edges.- Area and volume :... |
80 | 368 | 480 | 192 |
| [21] | omnitruncated 16-cell (also omnitruncated 8-cell) (gidpith) |
 |
t0,1,2,3{3,3,4} |
(1) (4.6.8) Truncated cuboctahedron In geometry, the truncated cuboctahedron is an Archimedean solid. It has 12 square faces, 8 regular hexagonal faces, 6 regular octagonal faces, 48 vertices and 72 edges... |
(1) (4.4.8) Octagonal prism In geometry, the octagonal prism is the sixth in an infinite set of prisms, formed by square sides and two regular octagon caps.If faces are all regular, it is a semiregular polyhedron.- Use :... |
(1) (4.4.6) Hexagonal prism In geometry, the hexagonal prism is a prism with hexagonal base. The shape has 8 faces, 18 edges, and 12 vertices.Since it has eight faces, it is an octahedron. However, the term octahedron is primarily used to refer to the regular octahedron, which has eight triangular faces... |
(1) (4.6.6) Truncated octahedron In geometry, the truncated octahedron is an Archimedean solid. It has 14 faces , 36 edges, and 24 vertices. Since each of its faces has point symmetry the truncated octahedron is a zonohedron.... |
80 | 464 | 768 | 384 |
| [31] | alternated cantitruncated 16-cell (Same as the snub 24-cell Snub 24-cell In geometry, the snub 24-cell is a convex uniform polychoron composed of 120 regular tetrahedral and 24 icosahedral cells. Five tetrahedra and three icosahedra meet at each vertex. In total it has 480 triangular faces, 432 edges, and 96 vertices.... ) (sadi) |
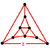 |
h0,1,2{3,3,4} |
(1) (3.3.3.3.3) Icosahedron In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids.... |
(1) (3.3.3) Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids... |
(4) (96) (96)(3.3.3) Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids... |
(2) (3.3.3.3.3) Icosahedron In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids.... |
144 | 480 | 432 | 96 |
Just as rectifying the tetrahedron
Tetrahedron
In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...
produces the octahedron
Octahedron
In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....
, rectifying the 16-cell produces the 24-cell, the regular member of the following family.
The snub 24-cell is repeat to this family for completeness. It is an alternation of the cantitruncated 16-cell or truncated 24-cell, with the half symmetry group [(3,3)+,4]. The truncated octahedral cells become icosahedra. The cube becomes a tetrahedron, and 96 new tetrahedra are created in the gaps from the removed vertices.
Graphs
The pictures are drawn as Schlegel diagram perspective projections, centered on the cell at pos. 3, with a consistent orientation, and the 16 cells at position 0 are shown solid, alternately colored.| # | Johnson Name (Bowers style acronym) |
Coxeter plane projections | Schlegel diagrams |
|||||
|---|---|---|---|---|---|---|---|---|
| F4 [12/3] |
B4 [8] |
B3 [6] |
B2 [4] |
A3 [4] |
Cube centered |
Tetrahedron centered |
||
| 10 | 8-cell or tesseract Tesseract In geometry, the tesseract, also called an 8-cell or regular octachoron or cubic prism, is the four-dimensional analog of the cube. The tesseract is to the cube as the cube is to the square. Just as the surface of the cube consists of 6 square faces, the hypersurface of the tesseract consists of 8... (tes) |
 |
||||||
| 11 | rectified 8-cell Rectified tesseract In geometry, the rectified tesseract, or rectified 8-cell is a uniform polychoron bounded by 24 cells: 8 cuboctahedra, and 16 tetrahedra.... (rit) |
 |
||||||
| 12 | 16-cell 16-cell In four dimensional geometry, a 16-cell or hexadecachoron is a regular convex 4-polytope. It is one of the six regular convex 4-polytopes first described by the Swiss mathematician Ludwig Schläfli in the mid-19th century.... (hex) |
 |
||||||
| 13 | truncated 8-cell Truncated tesseract In geometry, a truncated tesseract is a uniform polychoron formed as the truncation of the regular tesseract.There are three trunctions, including a bitruncation, and a tritruncation, which creates the truncated 16-cell.... (tat) |
 |
||||||
| 14 | cantellated 8-cell Cantellated tesseract In four-dimensional geometry, a cantellated tesseract is a convex uniform polychoron, being a cantellation of the regular tesseract.There are four degrees of cantellations of the tesseract including with permutations truncations... (srit) |
 |
||||||
| 15 | runcinated 8-cell Runcinated tesseract In four-dimensional geometry, a runcinated tesseract is a convex uniform polychoron, being a runcination of the regular tesseract.... (also runcinated 16-cell) (sidpith) |
 |
 |
|||||
| 16 | bitruncated 8-cell (also bitruncated 16-cell) (tah) |
 |
 |
|||||
| 17 | truncated 16-cell (thex) |  |
||||||
| 18 | cantitruncated 8-cell (grit) | 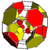 |
||||||
| 19 | runcitruncated 8-cell (proh) |  |
||||||
| 20 | runcitruncated 16-cell (prit) | 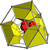 |
||||||
| 21 | omnitruncated 8-cell (also omnitruncated 16-cell) (gidpith) |
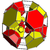 |
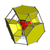 |
|||||
| [22] | *rectified 16-cell (Same as 24-cell) (ico) |
 |
||||||
| [23] | *cantellated 16-cell (Same as rectified 24-cell Rectified 24-cell In geometry, the rectified 24-cell is a uniform 4-dimensional polytope , which is bounded by 48 cells: 24 cubes, and 24 cuboctahedra. It can be obtained by reducing the icositetrachoron's cells to cubes or cuboctahedra.... ) (rico) |
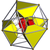 |
||||||
| [24] | *cantitruncated 16-cell (Same as truncated 24-cell Truncated 24-cell In geometry, a truncated 5-cell is a uniform polychoron formed as the truncation of the regular 5-cell.There are two degrees of trunctions, including a bitruncation.- Truncated 5-cell:... ) (tico) |
 |
||||||
| [31] | alternated cantitruncated 16-cell (Same as the snub 24-cell Snub 24-cell In geometry, the snub 24-cell is a convex uniform polychoron composed of 120 regular tetrahedral and 24 icosahedral cells. Five tetrahedra and three icosahedra meet at each vertex. In total it has 480 triangular faces, 432 edges, and 96 vertices.... ) (sadi) |
 |
Coordinates
The tesseractic family of polychora are given by the convex hulls of the base points listed in the following table, with all permutations of coordinates and sign taken. Each base point generates a distinct uniform polychora. All coordinates correspond with uniform polychora of edge length 2.| # | Base point | Johnson Name Bowers Name (Bowers style acronym) |
Coxeter-Dynkin Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... |
|---|---|---|---|
| 1 | (0,0,0,1)√2 | 16-cell 16-cell In four dimensional geometry, a 16-cell or hexadecachoron is a regular convex 4-polytope. It is one of the six regular convex 4-polytopes first described by the Swiss mathematician Ludwig Schläfli in the mid-19th century.... Hexadecachoron (hex) |
|
| 2 | (0,0,1,1)√2 | Rectified 16-cell Icositetrachoron (ico) |
|
| 3 | (0,0,1,2)√2 | Truncated 16-cell Truncated hexadecachoron (thex) |
|
| 4 | (0,1,1,1)√2 | Rectified tesseract Rectified tesseract In geometry, the rectified tesseract, or rectified 8-cell is a uniform polychoron bounded by 24 cells: 8 cuboctahedra, and 16 tetrahedra.... (birectified 16-cell) Rectified tesseract (rit) |
|
| 5 | (0,1,1,2)√2 | Cantellated 16-cell Rectified icositetrachoron (rico) |
|
| 6 | (0,1,2,2)√2 | Bitruncated 16-cell Tesseractihexadecachoron (tah) |
|
| 7 | (0,1,2,3)√2 | cantitruncated 16-cell Truncated icositetrachoron (tico) |
|
| 8 | (1,1,1,1) | Tesseract Tesseract In geometry, the tesseract, also called an 8-cell or regular octachoron or cubic prism, is the four-dimensional analog of the cube. The tesseract is to the cube as the cube is to the square. Just as the surface of the cube consists of 6 square faces, the hypersurface of the tesseract consists of 8... Tesseract (tes) |
|
| 9 | (1,1,1,1) + (0,0,0,1)√2 | Runcinated tesseract Runcinated tesseract In four-dimensional geometry, a runcinated tesseract is a convex uniform polychoron, being a runcination of the regular tesseract.... (runcinated 16-cell) Small disprismatotesseractihexadecachoron (sidpith) |
|
| 10 | (1,1,1,1) + (0,0,1,1)√2 | Cantellated tesseract Cantellated tesseract In four-dimensional geometry, a cantellated tesseract is a convex uniform polychoron, being a cantellation of the regular tesseract.There are four degrees of cantellations of the tesseract including with permutations truncations... Small rhombated tesseract (srit) |
|
| 11 | (1,1,1,1) + (0,0,1,2)√2 | Runcitruncated 16-cell Prismatorhombated tesseract (prit) |
|
| 12 | (1,1,1,1) + (0,1,1,1)√2 | Truncated tesseract Truncated tesseract In geometry, a truncated tesseract is a uniform polychoron formed as the truncation of the regular tesseract.There are three trunctions, including a bitruncation, and a tritruncation, which creates the truncated 16-cell.... Truncated tesseract (tat) |
|
| 13 | (1,1,1,1) + (0,1,1,2)√2 | Runcitruncated tesseract (runcicantellated 16-cell) Prismatorhombated hexadecachoron (proh) |
|
| 14 | (1,1,1,1) + (0,1,2,2)√2 | Cantitruncated tesseract Great rhombated tesseract (grit) |
|
| 15 | (1,1,1,1) + (0,1,2,3)√2 | Omnitruncated 16-cell (omnitruncated tesseract) Great disprismatotesseractihexadecachoron (gidpith) |
The F4 family
This family has diploid icositetrachoric symmetry, of order 24*48=1152: the 48 symmetries of the octahedron for each of the 24 cells.| # | Name | Vertex figure Vertex figure In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:... |
Coxeter-Dynkin Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... and Schläfli symbols |
Cell counts by location | Element counts | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
(24) |
(96) |
(96) |
(24) |
Cells | Faces | Edges | Vertices | ||||
| 22 | 24-cell (Same as rectified 16-cell) (ico) |
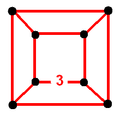 |
{3,4,3} |
(6) (3.3.3.3) Octahedron In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex.... |
24 | 96 | 96 | 24 | |||
| 23 | rectified 24-cell Rectified 24-cell In geometry, the rectified 24-cell is a uniform 4-dimensional polytope , which is bounded by 48 cells: 24 cubes, and 24 cuboctahedra. It can be obtained by reducing the icositetrachoron's cells to cubes or cuboctahedra.... (Same as cantellated 16-cell) (rico) |
 |
t1{3,4,3} |
(3) (3.4.3.4) Cuboctahedron In geometry, a cuboctahedron is a polyhedron with eight triangular faces and six square faces. A cuboctahedron has 12 identical vertices, with two triangles and two squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such it is a quasiregular polyhedron,... |
(2) (4.4.4) Cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and... |
48 | 240 | 288 | 96 | ||
| 24 | truncated 24-cell Truncated 24-cell In geometry, a truncated 5-cell is a uniform polychoron formed as the truncation of the regular 5-cell.There are two degrees of trunctions, including a bitruncation.- Truncated 5-cell:... (Same as cantitruncated 16-cell) (tico) |
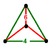 |
t0,1{3,4,3} |
(3) (4.6.6) Truncated octahedron In geometry, the truncated octahedron is an Archimedean solid. It has 14 faces , 36 edges, and 24 vertices. Since each of its faces has point symmetry the truncated octahedron is a zonohedron.... |
(1) (4.4.4) Cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and... |
48 | 240 | 384 | 192 | ||
| 25 | cantellated 24-cell Cantellated 24-cell In four-dimensional geometry, a cantellated 24-cell is a convex uniform polychoron, being a cantellation of the regular 24-cell.There are 2 unique degrees of runcinations of the 24-cell including with permutations truncations.... (srico) |
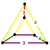 |
t0,2{3,4,3} |
(2) (3.4.4.4) |
(2) (3.4.4) Triangular prism In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides.... |
(1) (3.4.3.4) Cuboctahedron In geometry, a cuboctahedron is a polyhedron with eight triangular faces and six square faces. A cuboctahedron has 12 identical vertices, with two triangles and two squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such it is a quasiregular polyhedron,... |
144 | 720 | 864 | 288 | |
| 26 | *runcinated 24-cell Runcinated 24-cell In four-dimensional geometry, a runcinated 24-cell is a convex uniform polychoron, being a runcination of the regular 24-cell.... (spic) |
 |
t0,3{3,4,3} |
(1) (3.3.3.3) Octahedron In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex.... |
(3) (3.4.4) Triangular prism In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides.... |
(3) (3.4.4) Triangular prism In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides.... |
(1) (3.3.3.3) Octahedron In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex.... |
240 | 672 | 576 | 144 |
| 27 | *bitruncated 24-cell (cont) | 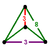 |
t1,2{3,4,3} |
(2) (3.8.8) Truncated cube In geometry, the truncated cube, or truncated hexahedron, is an Archimedean solid. It has 14 regular faces , 36 edges, and 24 vertices.... |
(2) (3.8.8) Truncated cube In geometry, the truncated cube, or truncated hexahedron, is an Archimedean solid. It has 14 regular faces , 36 edges, and 24 vertices.... |
48 | 336 | 576 | 288 | ||
| 28 | cantitruncated 24-cell (grico) | 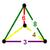 |
t0,1,2{3,4,3} |
(2) (4.6.8) Truncated cuboctahedron In geometry, the truncated cuboctahedron is an Archimedean solid. It has 12 square faces, 8 regular hexagonal faces, 6 regular octagonal faces, 48 vertices and 72 edges... |
(1) (3.4.4) Triangular prism In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides.... |
(1) (3.8.8) Truncated cube In geometry, the truncated cube, or truncated hexahedron, is an Archimedean solid. It has 14 regular faces , 36 edges, and 24 vertices.... |
144 | 720 | 1152 | 576 | |
| 29 | runcitruncated 24-cell (prico) |  |
t0,1,3{3,4,3} |
(1) (4.6.6) Truncated octahedron In geometry, the truncated octahedron is an Archimedean solid. It has 14 faces , 36 edges, and 24 vertices. Since each of its faces has point symmetry the truncated octahedron is a zonohedron.... |
(2) (4.4.6) Hexagonal prism In geometry, the hexagonal prism is a prism with hexagonal base. The shape has 8 faces, 18 edges, and 12 vertices.Since it has eight faces, it is an octahedron. However, the term octahedron is primarily used to refer to the regular octahedron, which has eight triangular faces... |
(1) (3.4.4) Triangular prism In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides.... |
(1) (3.4.4.4) |
240 | 1104 | 1440 | 576 |
| 30 | *omnitruncated 24-cell (gippic) |  |
t0,1,2,3{3,4,3} |
(1) (4.6.8) Truncated cuboctahedron In geometry, the truncated cuboctahedron is an Archimedean solid. It has 12 square faces, 8 regular hexagonal faces, 6 regular octagonal faces, 48 vertices and 72 edges... |
(1) (4.4.6) Hexagonal prism In geometry, the hexagonal prism is a prism with hexagonal base. The shape has 8 faces, 18 edges, and 12 vertices.Since it has eight faces, it is an octahedron. However, the term octahedron is primarily used to refer to the regular octahedron, which has eight triangular faces... |
(1) (4.4.6) Hexagonal prism In geometry, the hexagonal prism is a prism with hexagonal base. The shape has 8 faces, 18 edges, and 12 vertices.Since it has eight faces, it is an octahedron. However, the term octahedron is primarily used to refer to the regular octahedron, which has eight triangular faces... |
(1) (4.6.8) Truncated cuboctahedron In geometry, the truncated cuboctahedron is an Archimedean solid. It has 12 square faces, 8 regular hexagonal faces, 6 regular octagonal faces, 48 vertices and 72 edges... |
240 | 1392 | 2304 | 1152 |
| 31 | Alternated truncated 24-cell †(Same as snub 24-cell Snub 24-cell In geometry, the snub 24-cell is a convex uniform polychoron composed of 120 regular tetrahedral and 24 icosahedral cells. Five tetrahedra and three icosahedra meet at each vertex. In total it has 480 triangular faces, 432 edges, and 96 vertices.... ) (sadi) |
 |
h0,1{3,4,3} |
(3) (3.3.3.3.3) Icosahedron In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids.... |
(4) (3.3.3) Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids... |
(1) (3.3.3) Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids... |
144 | 480 | 432 | 96 |
- (*) Like the 5-cell, the 24-cell is self-dual, and so the three asterisked forms have twice as many symmetries, bringing their total to 2304 (the extended icositetrachoric group
3,4,3 ). - (†) The snub 24-cell here, despite its common name, is not analogous to the snub cubeSnub cubeIn geometry, the snub cube, or snub cuboctahedron, is an Archimedean solid.The snub cube has 38 faces, 6 of which are squares and the other 32 are equilateral triangles. It has 60 edges and 24 vertices. It is a chiral polyhedron, that is, it has two distinct forms, which are mirror images of each...
; rather, is derived by an alternation of the truncated 24-cell. Its symmetry numberSymmetry numberThe symmetry number or symmetry order of an object is the number of different but indistinguishable arrangements of the object, i.e. the order of its symmetry group...
is only 576, (the ionic diminished icositetrachoric group, [3+,4,3]).
Graphs
| # | Name Coxeter-Dynkin Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... Schläfli symbol |
Graph |
Schlegel diagram |
Orthogonal Projection |
||||
|---|---|---|---|---|---|---|---|---|
| F4 [12] |
B4 [8] |
B3 [6] |
B2 [4] |
Octahedron centered |
Dual octahedron centered |
Octahedron centered |
||
| 22 | 24-cell (ico) (rectified 16-cell) {3,4,3} |
 |
||||||
| 23 | rectified 24-cell Rectified 24-cell In geometry, the rectified 24-cell is a uniform 4-dimensional polytope , which is bounded by 48 cells: 24 cubes, and 24 cuboctahedra. It can be obtained by reducing the icositetrachoron's cells to cubes or cuboctahedra.... (rico) (cantellated 16-cell) t1{3,4,3} |
 |
||||||
| 24 | truncated 24-cell Truncated 24-cell In geometry, a truncated 5-cell is a uniform polychoron formed as the truncation of the regular 5-cell.There are two degrees of trunctions, including a bitruncation.- Truncated 5-cell:... (tico) (cantitruncated 16-cell) t0,1{3,4,3} |
 |
||||||
| 25 | cantellated 24-cell Cantellated 24-cell In four-dimensional geometry, a cantellated 24-cell is a convex uniform polychoron, being a cantellation of the regular 24-cell.There are 2 unique degrees of runcinations of the 24-cell including with permutations truncations.... (srico) t0,2{3,4,3} |
 |
||||||
| 26 | *runcinated 24-cell Runcinated 24-cell In four-dimensional geometry, a runcinated 24-cell is a convex uniform polychoron, being a runcination of the regular 24-cell.... (spic) t0,3{3,4,3} |
|||||||
| 27 | *bitruncated 24-cell (cont) t1,2{3,4,3} |
|||||||
| 28 | cantitruncated 24-cell (grico) t0,1,2{3,4,3} |
|||||||
| 29 | runcitruncated 24-cell (prico) t0,1,3{3,4,3} |
 |
||||||
| 30 | *omnitruncated 24-cell (gippic) t0,1,2,3{3,4,3} |
 |
||||||
| 31 | Alternated truncated 24-cell †(Same as snub 24-cell Snub 24-cell In geometry, the snub 24-cell is a convex uniform polychoron composed of 120 regular tetrahedral and 24 icosahedral cells. Five tetrahedra and three icosahedra meet at each vertex. In total it has 480 triangular faces, 432 edges, and 96 vertices.... ) (sadi) h0,1{3,4,3} |
 |
 |
|||||
Coordinates
Vertex coordinates for all 15 forms are given below, including dual configurations from the two regular 24-cells. (The dual configurations are named in bold.) Active rings in the first and second nodes generate points in the first column. Active rings in the third and fourth nodes generate the points in the second column. The sum of each of these points are then permutated by coordinate positions, and sign combinations. This generates all vertex coordinates. Edge lengths are 2.The only exception is the snub 24-cell, which is generated by half of the coordinate permutations, only an even number of coordinate swaps. φ=(√5+1)/2.
| Base point(s) t(0,1) |
Base point(s) t(2,3) |
Schläfli symbol | Name |
Coxeter-Dynkin Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... |
|---|---|---|---|---|
| (0,0,1,1)√2 | t0{3,4,3} | 24-cell | ||
| (0,1,1,2)√2 | t1{3,4,3} | Rectified 24-cell Rectified 24-cell In geometry, the rectified 24-cell is a uniform 4-dimensional polytope , which is bounded by 48 cells: 24 cubes, and 24 cuboctahedra. It can be obtained by reducing the icositetrachoron's cells to cubes or cuboctahedra.... |
||
| (0,1,2,3)√2 | t0,1{3,4,3} | Truncated 24-cell Truncated 24-cell In geometry, a truncated 5-cell is a uniform polychoron formed as the truncation of the regular 5-cell.There are two degrees of trunctions, including a bitruncation.- Truncated 5-cell:... |
||
| (0,1,φ,φ+1)√2 | h0,1{3,4,3} | Snub 24-cell Snub 24-cell In geometry, the snub 24-cell is a convex uniform polychoron composed of 120 regular tetrahedral and 24 icosahedral cells. Five tetrahedra and three icosahedra meet at each vertex. In total it has 480 triangular faces, 432 edges, and 96 vertices.... |
||
| (0,2,2,2) (1,1,1,3) |
t2{3,4,3} | Birectified 24-cell (Rectified 24-cell Rectified 24-cell In geometry, the rectified 24-cell is a uniform 4-dimensional polytope , which is bounded by 48 cells: 24 cubes, and 24 cuboctahedra. It can be obtained by reducing the icositetrachoron's cells to cubes or cuboctahedra.... ) |
||
| (0,2,2,2) + (1,1,1,3) + |
(0,0,1,1)√2 " |
t0,2{3,4,3} | Cantellated 24-cell Cantellated 24-cell In four-dimensional geometry, a cantellated 24-cell is a convex uniform polychoron, being a cantellation of the regular 24-cell.There are 2 unique degrees of runcinations of the 24-cell including with permutations truncations.... |
|
| (0,2,2,2) + (1,1,1,3) + |
(0,1,1,2)√2 " |
t1,2{3,4,3} | Bitruncated 24-cell | |
| (0,2,2,2) + (1,1,1,3) + |
(0,1,2,3)√2 " |
t0,1,2{3,4,3} | Cantitruncated 24-cell | |
| (0,0,0,2) (1,1,1,1) |
t3{3,4,3} | Trirectified 24-cell (24-cell) |
||
| (0,0,0,2) + (1,1,1,1) + |
(0,0,1,1)√2 " |
t0,3{3,4,3} | Runcinated 24-cell Runcinated 24-cell In four-dimensional geometry, a runcinated 24-cell is a convex uniform polychoron, being a runcination of the regular 24-cell.... |
|
| (0,0,0,2) + (1,1,1,1) + |
(0,1,1,2)√2 " |
t1,3{3,4,3} | bicantellated 24-cell (Cantellated 24-cell Cantellated 24-cell In four-dimensional geometry, a cantellated 24-cell is a convex uniform polychoron, being a cantellation of the regular 24-cell.There are 2 unique degrees of runcinations of the 24-cell including with permutations truncations.... ) |
|
| (0,0,0,2) + (1,1,1,1) + |
(0,1,2,3)√2 " |
t0,1,3{3,4,3} | Runcitruncated 24-cell | |
| (1,1,1,5) (1,3,3,3) (2,2,2,4) |
t2,3{3,4,3} | Tritruncated 24-cell (Truncated 24-cell Truncated 24-cell In geometry, a truncated 5-cell is a uniform polychoron formed as the truncation of the regular 5-cell.There are two degrees of trunctions, including a bitruncation.- Truncated 5-cell:... ) |
||
| (1,1,1,5) + (1,3,3,3) + (2,2,2,4) + |
(0,0,1,1)√2 " " |
t0,2,3{3,4,3} | Runcicantellated 24-cell (Runcitruncated 24-cell) |
|
| (1,1,1,5) + (1,3,3,3) + (2,2,2,4) + |
(0,1,1,2)√2 " " |
t1,2,3{3,4,3} | Bicantitruncated 24-cell (Cantitruncated 24-cell) |
|
| (1,1,1,5) + (1,3,3,3) + (2,2,2,4) + |
(0,1,2,3)√2 " " |
t0,1,2,3{3,4,3} | Omnitruncated 24-cell | |
The H4 family
This family has diploid hexacosichoric symmetry, of order 120*120=24*600=14400: 120 for each of the 120 dodecahedra, or 24 for each of the 600 tetrahedra.120-cell truncations
| # | Johnson Name (Bowers style Acronym) |
Vertex figure Vertex figure In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:... |
Coxeter-Dynkin Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... and Schläfli symbols |
Cell counts by location | Element counts | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
(120) |
(720) |
(1200) |
(600) |
Cells | Faces | Edges | Vertices | ||||
| 32 | 120-cell (hi) |  |
{5,3,3} |
(4) (5.5.5) |
120 | 720 | 1200 | 600 | |||
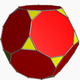
| 33 | rectified 120-cell Rectified 120-cell In geometry, a rectified 120-cell is a uniform polychoron formed as the rectification of the regular 120-cell.There are four rectifications of the 120-cell, including the zeroth, the 120-cell itself... (rahi) |
 |
t1{5,3,3} |
(3) (3.5.3.5) Icosidodecahedron In geometry, an icosidodecahedron is a polyhedron with twenty triangular faces and twelve pentagonal faces. An icosidodecahedron has 30 identical vertices, with two triangles and two pentagons meeting at each, and 60 identical edges, each separating a triangle from a pentagon... |
(2) (3.3.3) Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids... |
720 | 3120 | 3600 | 1200 | ||
| 36 | truncated 120-cell Truncated 120-cell In geometry, a truncated 120-cell is a uniform polychoron formed as the truncation of the regular 120-cell.There are three trunctions, including a bitruncation, and a tritruncation, which creates the truncated 600-cell.... (thi) |
 |
t0,1{5,3,3} |
(3) (3.10.10) Truncated dodecahedron In geometry, the truncated dodecahedron is an Archimedean solid. It has 12 regular decagonal faces, 20 regular triangular faces, 60 vertices and 90 edges.- Geometric relations :... |
(1) (3.3.3) Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids... |
720 | 3120 | 4800 | 2400 | ||
| 37 | cantellated 120-cell Cantellated 120-cell In four-dimensional geometry, a cantellated 120-cell is a convex uniform polychoron, being a cantellation of the regular 120-cell.... (srahi) |
 |
t0,2{5,3,3} |
(1) (3.4.5.4) |
(2) (3.4.4) Triangular prism In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides.... |
(1) (3.3.3.3) Octahedron In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex.... |
1920 | 9120 | 10800 | 3600 | |
| 38 | runcinated 120-cell Runcinated 120-cell In four-dimensional geometry, a runcinated 120-cell is a convex uniform polychoron, being a runcination of the regular 120-cell.... (also runcinated 600-cell) (sidpixhi) |
 |
t0,3{5,3,3} |
(1) (5.5.5) |
(3) (4.4.5) Pentagonal prism In geometry, the pentagonal prism is a prism with a pentagonal base. It is a type of heptahedron with 7 faces, 15 edges, and 10 vertices.- As a semiregular polyhedron :... |
(3) (3.4.4) Triangular prism In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides.... |
(1) (3.3.3) Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids... |
2640 | 7440 | 7200 | 2400 |
| 39 | bitruncated 120-cell (also bitruncated 600-cell) (xhi) |
 |
t1,2{5,3,3} |
(2)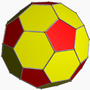 (5.6.6) Truncated icosahedron In geometry, the truncated icosahedron is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids whose faces are two or more types of regular polygons.It has 12 regular pentagonal faces, 20 regular hexagonal faces, 60 vertices and 90 edges.... |
(2) (3.6.6) Truncated tetrahedron In geometry, the truncated tetrahedron is an Archimedean solid. It has 4 regular hexagonal faces, 4 regular triangular faces, 12 vertices and 18 edges.- Area and volume :... |
720 | 4320 | 7200 | 3600 | ||
| 42 | cantitruncated 120-cell (grahi) |  |
t0,1,2{5,3,3} |
(2)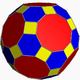 (4.6.10) Truncated icosidodecahedron In geometry, the truncated icosidodecahedron is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids constructed by two or more types of regular polygon faces.... |
(1) (3.4.4) Triangular prism In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides.... |
(1) (3.6.6) Truncated tetrahedron In geometry, the truncated tetrahedron is an Archimedean solid. It has 4 regular hexagonal faces, 4 regular triangular faces, 12 vertices and 18 edges.- Area and volume :... |
1920 | 9120 | 14400 | 7200 | |
| 43 | runcitruncated 120-cell (prix) |  |
t0,1,3{5,3,3} |
(1) (3.10.10) Truncated dodecahedron In geometry, the truncated dodecahedron is an Archimedean solid. It has 12 regular decagonal faces, 20 regular triangular faces, 60 vertices and 90 edges.- Geometric relations :... |
(2) (4.4.10) Decagonal prism In geometry, the decagonal prism is the eighth in an infinite set of prisms, formed by ten square side faces and two regular decagon caps. With twelve faces, it is one of many nonregular dodecahedra.If faces are all regular, it is a semiregular polyhedron.... |
(1) (3.4.4) Triangular prism In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides.... |
(1) (3.4.3.4) Cuboctahedron In geometry, a cuboctahedron is a polyhedron with eight triangular faces and six square faces. A cuboctahedron has 12 identical vertices, with two triangles and two squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such it is a quasiregular polyhedron,... |
2640 | 13440 | 18000 | 7200 |
| 46 | omnitruncated 120-cell (also omnitruncated 600-cell) (gidpixhi) |
 |
t0,1,2,3{5,3,3} |
(1) (4.6.10) Truncated icosidodecahedron In geometry, the truncated icosidodecahedron is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids constructed by two or more types of regular polygon faces.... |
(1) (4.4.10) Decagonal prism In geometry, the decagonal prism is the eighth in an infinite set of prisms, formed by ten square side faces and two regular decagon caps. With twelve faces, it is one of many nonregular dodecahedra.If faces are all regular, it is a semiregular polyhedron.... |
(1) (4.4.6) Hexagonal prism In geometry, the hexagonal prism is a prism with hexagonal base. The shape has 8 faces, 18 edges, and 12 vertices.Since it has eight faces, it is an octahedron. However, the term octahedron is primarily used to refer to the regular octahedron, which has eight triangular faces... |
(1) (4.6.6) Truncated octahedron In geometry, the truncated octahedron is an Archimedean solid. It has 14 faces , 36 edges, and 24 vertices. Since each of its faces has point symmetry the truncated octahedron is a zonohedron.... |
2640 | 17040 | 28800 | 14400 |
600-cell truncations
| # | Johnson Name (Bowers style acronym) |
Vertex figure Vertex figure In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:... |
Coxeter-Dynkin Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... and Schläfli symbols |
Cell counts by location | Element counts | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
(120) |
(720) |
(1200) |
(600) |
Cells | Faces | Edges | Vertices | ||||
| 35 | 600-cell (ex) |  |
{3,3,5} |
(20) (3.3.3) Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids... |
600 | 1200 | 720 | 120 | |||
| 34 | rectified 600-cell Rectified 600-cell In geometry, a rectified 600-cell is a uniform polychoron formed as the rectification of the regular 600-cell.There are four rectifications of the 600-cell, including the zeroth, the 600-cell itself... (rox) |
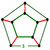 |
t1{3,3,5} |
(2) (3.3.3.3.3) Icosahedron In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids.... |
(5) (3.3.3.3) Octahedron In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex.... |
720 | 3600 | 3600 | 720 | ||
| 41 | truncated 600-cell (tex) | 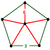 |
t0,1{3,3,5} |
(1) (3.3.3.3.3) Icosahedron In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids.... |
(5) (3.6.6) Truncated tetrahedron In geometry, the truncated tetrahedron is an Archimedean solid. It has 4 regular hexagonal faces, 4 regular triangular faces, 12 vertices and 18 edges.- Area and volume :... |
720 | 3600 | 4320 | 1440 | ||
| 40 | cantellated 600-cell (srix) | 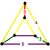 |
t0,2{3,3,5} |
(1) (3.5.3.5) Icosidodecahedron In geometry, an icosidodecahedron is a polyhedron with twenty triangular faces and twelve pentagonal faces. An icosidodecahedron has 30 identical vertices, with two triangles and two pentagons meeting at each, and 60 identical edges, each separating a triangle from a pentagon... |
(2) (4.4.5) Pentagonal prism In geometry, the pentagonal prism is a prism with a pentagonal base. It is a type of heptahedron with 7 faces, 15 edges, and 10 vertices.- As a semiregular polyhedron :... |
(1) (3.4.3.4) Cuboctahedron In geometry, a cuboctahedron is a polyhedron with eight triangular faces and six square faces. A cuboctahedron has 12 identical vertices, with two triangles and two squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such it is a quasiregular polyhedron,... |
1440 | 8640 | 10800 | 3600 | |
| [38] | runcinated 600-cell (also runcinated 120-cell) (sidpixhi) |
 |
t0,3{3,3,5} |
(1) (5.5.5) |
(3) (4.4.5) Pentagonal prism In geometry, the pentagonal prism is a prism with a pentagonal base. It is a type of heptahedron with 7 faces, 15 edges, and 10 vertices.- As a semiregular polyhedron :... |
(3) (3.4.4) Triangular prism In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides.... |
(1) (3.3.3) Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids... |
2640 | 7440 | 7200 | 2400 |
| [39] | bitruncated 600-cell (also bitruncated 120-cell) (xhi) |
 |
t1,2{3,3,5} |
(2) (5.6.6) Truncated icosahedron In geometry, the truncated icosahedron is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids whose faces are two or more types of regular polygons.It has 12 regular pentagonal faces, 20 regular hexagonal faces, 60 vertices and 90 edges.... |
(2) (3.6.6) Truncated tetrahedron In geometry, the truncated tetrahedron is an Archimedean solid. It has 4 regular hexagonal faces, 4 regular triangular faces, 12 vertices and 18 edges.- Area and volume :... |
720 | 4320 | 7200 | 3600 | ||
| 45 | cantitruncated 600-cell (grix) | 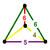 |
t0,1,2{3,3,5} |
(1) (5.6.6) Truncated icosahedron In geometry, the truncated icosahedron is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids whose faces are two or more types of regular polygons.It has 12 regular pentagonal faces, 20 regular hexagonal faces, 60 vertices and 90 edges.... |
(1) (4.4.5) Pentagonal prism In geometry, the pentagonal prism is a prism with a pentagonal base. It is a type of heptahedron with 7 faces, 15 edges, and 10 vertices.- As a semiregular polyhedron :... |
(2) (4.6.6) Truncated octahedron In geometry, the truncated octahedron is an Archimedean solid. It has 14 faces , 36 edges, and 24 vertices. Since each of its faces has point symmetry the truncated octahedron is a zonohedron.... |
1440 | 8640 | 14400 | 7200 | |
| 44 | runcitruncated 600-cell (prahi) |  |
t0,1,3{3,3,5} |
(1) (3.4.5.4) |
(1) (4.4.5) Pentagonal prism In geometry, the pentagonal prism is a prism with a pentagonal base. It is a type of heptahedron with 7 faces, 15 edges, and 10 vertices.- As a semiregular polyhedron :... |
(2) (4.4.6) Hexagonal prism In geometry, the hexagonal prism is a prism with hexagonal base. The shape has 8 faces, 18 edges, and 12 vertices.Since it has eight faces, it is an octahedron. However, the term octahedron is primarily used to refer to the regular octahedron, which has eight triangular faces... |
(1) (3.6.6) Truncated tetrahedron In geometry, the truncated tetrahedron is an Archimedean solid. It has 4 regular hexagonal faces, 4 regular triangular faces, 12 vertices and 18 edges.- Area and volume :... |
2640 | 13440 | 18000 | 7200 |
| [46] | omnitruncated 600-cell (also omnitruncated 120-cell) (gidpixhi) |
 |
t0,1,2,3{3,3,5} |
(1) (4.6.10) Truncated icosidodecahedron In geometry, the truncated icosidodecahedron is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids constructed by two or more types of regular polygon faces.... |
(1) (4.4.10) Decagonal prism In geometry, the decagonal prism is the eighth in an infinite set of prisms, formed by ten square side faces and two regular decagon caps. With twelve faces, it is one of many nonregular dodecahedra.If faces are all regular, it is a semiregular polyhedron.... |
(1) (4.4.6) Hexagonal prism In geometry, the hexagonal prism is a prism with hexagonal base. The shape has 8 faces, 18 edges, and 12 vertices.Since it has eight faces, it is an octahedron. However, the term octahedron is primarily used to refer to the regular octahedron, which has eight triangular faces... |
(1) (4.6.6) Truncated octahedron In geometry, the truncated octahedron is an Archimedean solid. It has 14 faces , 36 edges, and 24 vertices. Since each of its faces has point symmetry the truncated octahedron is a zonohedron.... |
2640 | 17040 | 28800 | 14400 |
Graphs
| # | Johnson Name (Bowers style Acronym) |
Coxeter plane projections | Schlegel diagrams | ||||||
|---|---|---|---|---|---|---|---|---|---|
| F4 [12] |
[20] | H4 [30] |
H3 [10] |
A3 [4] |
A2 [3] |
Dodecahedron centered |
Tetrahedron centered |
||
| 32 | 120-cell (hi) | 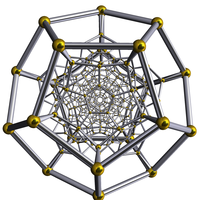 |
|||||||
| 33 | rectified 120-cell Rectified 120-cell In geometry, a rectified 120-cell is a uniform polychoron formed as the rectification of the regular 120-cell.There are four rectifications of the 120-cell, including the zeroth, the 120-cell itself... (rahi) |
||||||||
| 34 | rectified 600-cell Rectified 600-cell In geometry, a rectified 600-cell is a uniform polychoron formed as the rectification of the regular 600-cell.There are four rectifications of the 600-cell, including the zeroth, the 600-cell itself... (rox) |
||||||||
| 35 | 600-cell (ex) | 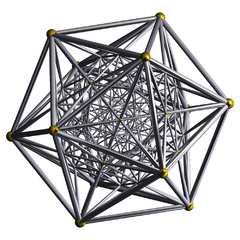 |
 |
||||||
| 36 | truncated 120-cell Truncated 120-cell In geometry, a truncated 120-cell is a uniform polychoron formed as the truncation of the regular 120-cell.There are three trunctions, including a bitruncation, and a tritruncation, which creates the truncated 600-cell.... (thi) |
 |
|||||||
| 37 | cantellated 120-cell Cantellated 120-cell In four-dimensional geometry, a cantellated 120-cell is a convex uniform polychoron, being a cantellation of the regular 120-cell.... (srahi) |
 |
|||||||
| 38 | runcinated 120-cell Runcinated 120-cell In four-dimensional geometry, a runcinated 120-cell is a convex uniform polychoron, being a runcination of the regular 120-cell.... (also runcinated 600-cell) (sidpixhi) |
 |
|||||||
| 39 | bitruncated 120-cell (also bitruncated 600-cell) (xhi) |
||||||||
| 40 | cantellated 600-cell (srix) |  |
|||||||
| 41 | truncated 600-cell (tex) |  |
|||||||
| 42 | cantitruncated 120-cell (grahi) |  |
|||||||
| 43 | runcitruncated 120-cell (prix) |  |
|||||||
| 44 | runcitruncated 600-cell (prahi) |  |
|||||||
| 45 | cantitruncated 600-cell (grix) |  |
|||||||
| 46 | omnitruncated 120-cell (also omnitruncated 600-cell) (gidpixhi) |
 |
The D4 family
This demitesseract family introduces no new uniform polychora, but it is worthy to repeat these alternative constructions.This family has order 12*16=192: 4!/2=12 permutations of the four axes, half as alternated, 24=16 for reflection in each axis.
| # | Johnson Name (Bowers style acronym) | Vertex figure Vertex figure In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:... |
Coxeter-Dynkin Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors...  |
Cell counts by location | Element counts | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
(8) |
(24) |
(8) |
(8) |
Pos. Alt (96) |
3 | 2 | 1 | 0 | ||||
| [12] | demitesseract (Same as 16-cell 16-cell In four dimensional geometry, a 16-cell or hexadecachoron is a regular convex 4-polytope. It is one of the six regular convex 4-polytopes first described by the Swiss mathematician Ludwig Schläfli in the mid-19th century.... ) (hex) |
 |
t0{31,1,1} |
(4) (3.3.3) Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids... |
(4) (3.3.3) Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids... |
16 | 32 | 24 | 8 | |||
| [17] | truncated demitesseract (Same as truncated 16-cell) (thex) |
 |
t0,1{31,1,1} |
(1) (3.3.3.3) Octahedron In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex.... |
(2) (3.6.6) Truncated tetrahedron In geometry, the truncated tetrahedron is an Archimedean solid. It has 4 regular hexagonal faces, 4 regular triangular faces, 12 vertices and 18 edges.- Area and volume :... |
(2) (3.6.6) Truncated tetrahedron In geometry, the truncated tetrahedron is an Archimedean solid. It has 4 regular hexagonal faces, 4 regular triangular faces, 12 vertices and 18 edges.- Area and volume :... |
24 | 96 | 120 | 48 | ||
| [11] | cantellated demitesseract (Same as rectified tesseract Rectified tesseract In geometry, the rectified tesseract, or rectified 8-cell is a uniform polychoron bounded by 24 cells: 8 cuboctahedra, and 16 tetrahedra.... ) (rit) |
 |
t0,2{31,1,1} |
(1) (3.3.3) Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids... |
(1) (3.3.3) Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids... |
(3) (3.4.3.4) Cuboctahedron In geometry, a cuboctahedron is a polyhedron with eight triangular faces and six square faces. A cuboctahedron has 12 identical vertices, with two triangles and two squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such it is a quasiregular polyhedron,... |
24 | 88 | 96 | 32 | ||
| [16] | cantitruncated demitesseract (Same as bitruncated tesseract) (tah) |
 |
t0,1,2{31,1,1} |
(1) (3.6.6) Truncated tetrahedron In geometry, the truncated tetrahedron is an Archimedean solid. It has 4 regular hexagonal faces, 4 regular triangular faces, 12 vertices and 18 edges.- Area and volume :... |
(1) (3.6.6) Truncated tetrahedron In geometry, the truncated tetrahedron is an Archimedean solid. It has 4 regular hexagonal faces, 4 regular triangular faces, 12 vertices and 18 edges.- Area and volume :... |
(2) (4.6.6) Truncated octahedron In geometry, the truncated octahedron is an Archimedean solid. It has 14 faces , 36 edges, and 24 vertices. Since each of its faces has point symmetry the truncated octahedron is a zonohedron.... |
24 | 96 | 96 | 24 | ||
| [22] | rectified demitesseract (Same as rectified 16-cell) (Same as 24-cell) (ico) |
 |
t1{31,1,1} |
(2) (3.3.3.3) Octahedron In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex.... |
(2) (3.3.3.3) Octahedron In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex.... |
(2) (3.3.3.3) Octahedron In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex.... |
48 | 240 | 288 | 96 | ||
| [23] | runcicantellated demitesseract (Same as cantellated 16-cell) (Same as rectified 24-cell Rectified 24-cell In geometry, the rectified 24-cell is a uniform 4-dimensional polytope , which is bounded by 48 cells: 24 cubes, and 24 cuboctahedra. It can be obtained by reducing the icositetrachoron's cells to cubes or cuboctahedra.... ) (rico) |
 |
t0,2,3{31,1,1} |
(1) (3.4.3.4) Cuboctahedron In geometry, a cuboctahedron is a polyhedron with eight triangular faces and six square faces. A cuboctahedron has 12 identical vertices, with two triangles and two squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such it is a quasiregular polyhedron,... |
(2) (4.4.4) Cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and... |
(1) (3.4.3.4) Cuboctahedron In geometry, a cuboctahedron is a polyhedron with eight triangular faces and six square faces. A cuboctahedron has 12 identical vertices, with two triangles and two squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such it is a quasiregular polyhedron,... |
(1) (3.4.3.4) Cuboctahedron In geometry, a cuboctahedron is a polyhedron with eight triangular faces and six square faces. A cuboctahedron has 12 identical vertices, with two triangles and two squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such it is a quasiregular polyhedron,... |
24 | 120 | 192 | 96 | |
| [24] | omnitruncated demitesseract (Same as cantitruncated 16-cell) (Same as truncated 24-cell Truncated 24-cell In geometry, a truncated 5-cell is a uniform polychoron formed as the truncation of the regular 5-cell.There are two degrees of trunctions, including a bitruncation.- Truncated 5-cell:... ) (tico) |
 |
t0,1,2,3{31,1,1} |
(1) (4.6.6) Truncated octahedron In geometry, the truncated octahedron is an Archimedean solid. It has 14 faces , 36 edges, and 24 vertices. Since each of its faces has point symmetry the truncated octahedron is a zonohedron.... |
(1) (4.4.4) Cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and... |
(1) (4.6.6) Truncated octahedron In geometry, the truncated octahedron is an Archimedean solid. It has 14 faces , 36 edges, and 24 vertices. Since each of its faces has point symmetry the truncated octahedron is a zonohedron.... |
(1) (4.6.6) Truncated octahedron In geometry, the truncated octahedron is an Archimedean solid. It has 14 faces , 36 edges, and 24 vertices. Since each of its faces has point symmetry the truncated octahedron is a zonohedron.... |
48 | 240 | 384 | 192 | |
| [31] | snub demitesseract (Same as snub 24-cell Snub 24-cell In geometry, the snub 24-cell is a convex uniform polychoron composed of 120 regular tetrahedral and 24 icosahedral cells. Five tetrahedra and three icosahedra meet at each vertex. In total it has 480 triangular faces, 432 edges, and 96 vertices.... ) (sadi) |
 |
s{31,1,1} |
(1) (3.3.3.3.3) Icosahedron In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids.... |
(1) (3.3.3) Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids... |
(1) (3.3.3.3.3) Icosahedron In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids.... |
(1) (3.3.3.3.3) Icosahedron In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids.... |
(4) (3.3.3) Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids... |
144 | 480 | 432 | 96 |
Here again the snub 24-cell, with the symmetry group [31,1,1]+ this time, represents an alternated truncation of the truncated 24-cell creating 96 new tetrahedra at the position of the deleted vertices. In contrast to its appearance within former groups as partly snubbed polychoron, only within this symmetry group it has the full analogy to the Kepler snubs, i.e. the snub cube
Snub cube
In geometry, the snub cube, or snub cuboctahedron, is an Archimedean solid.The snub cube has 38 faces, 6 of which are squares and the other 32 are equilateral triangles. It has 60 edges and 24 vertices. It is a chiral polyhedron, that is, it has two distinct forms, which are mirror images of each...
and the snub dodecahedron
Snub dodecahedron
In geometry, the snub dodecahedron, or snub icosidodecahedron, is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids constructed by two or more types of regular polygon faces....
.
Graphs
| # | Johnson Name (Bowers style acronym) Coxeter-Dynkin Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... |
Coxeter plane projections | Schlegel diagrams | Parallel 3D |
|||
|---|---|---|---|---|---|---|---|
| B4 [8/2] |
D4 [6] |
D3 [2] |
B3 [3,4] |
A3 [3,3] |
D4 [6] |
||
| [12] | demitesseract (Same as 16-cell 16-cell In four dimensional geometry, a 16-cell or hexadecachoron is a regular convex 4-polytope. It is one of the six regular convex 4-polytopes first described by the Swiss mathematician Ludwig Schläfli in the mid-19th century.... ) (hex) t0{31,1,1} |
 |
|||||
| [17] | truncated demitesseract (Same as truncated 16-cell) (thex) t0,1{31,1,1} |
 |
|||||
| [11] | cantellated demitesseract (Same as rectified tesseract Rectified tesseract In geometry, the rectified tesseract, or rectified 8-cell is a uniform polychoron bounded by 24 cells: 8 cuboctahedra, and 16 tetrahedra.... ) (rit) t0,2{31,1,1} |
 |
|||||
| [16] | cantitruncated demitesseract (Same as bitruncated tesseract) (tah) t0,1,2{31,1,1} |
 |
|||||
| [22] | rectified demitesseract (Same as rectified 16-cell) (Same as 24-cell) (ico) t1{31,1,1} |
 |
|||||
| [23] | runcicantellated demitesseract (Same as cantellated 16-cell) (Same as rectified 24-cell Rectified 24-cell In geometry, the rectified 24-cell is a uniform 4-dimensional polytope , which is bounded by 48 cells: 24 cubes, and 24 cuboctahedra. It can be obtained by reducing the icositetrachoron's cells to cubes or cuboctahedra.... ) (rico) t0,2,3{31,1,1} |
 |
|||||
| [24] | omnitruncated demitesseract (Same as cantitruncated 16-cell) (Same as truncated 24-cell Truncated 24-cell In geometry, a truncated 5-cell is a uniform polychoron formed as the truncation of the regular 5-cell.There are two degrees of trunctions, including a bitruncation.- Truncated 5-cell:... ) (tico) t0,1,2,3{31,1,1} |
 |
|||||
| [31] | Snub demitesseract (snub 24-cell Snub 24-cell In geometry, the snub 24-cell is a convex uniform polychoron composed of 120 regular tetrahedral and 24 icosahedral cells. Five tetrahedra and three icosahedra meet at each vertex. In total it has 480 triangular faces, 432 edges, and 96 vertices.... ) (sadi) s{31,1,1} |
 |
Coordinates
The base point can generate the coordinates of the polytope by taking all coordinate permutations and sign combinations. The edges' length will be √2. Some polytopes have two possible generator points. Points are prefixed by Even to imply only an even count of sign permutations should be included.| # | Base point | Johnson and Bowers Names | Coxeter-Dynkin Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... |
Related B4 Coxeter-Dynkin |
|---|---|---|---|---|
| [12] | (0,0,0,2) | 16-cell 16-cell In four dimensional geometry, a 16-cell or hexadecachoron is a regular convex 4-polytope. It is one of the six regular convex 4-polytopes first described by the Swiss mathematician Ludwig Schläfli in the mid-19th century.... |
||
| [22] | (0,0,2,2) | Rectified 16-cell | ||
| [17] | (0,0,2,4) | Truncated 16-cell | ||
| [11] | (0,2,2,2) | Cantellated 16-cell | ||
| [23] | (0,2,2,4) | Cantellated 16-cell | ||
| [16] | (0,2,4,4) | Bitruncated 16-cell | ||
| [24] | (0,2,4,6) | Cantitruncated 16-cell | ||
| [31] | (0,1,φ,φ+1)/√2 | snub 24-cell Snub 24-cell In geometry, the snub 24-cell is a convex uniform polychoron composed of 120 regular tetrahedral and 24 icosahedral cells. Five tetrahedra and three icosahedra meet at each vertex. In total it has 480 triangular faces, 432 edges, and 96 vertices.... |
||
| [12] | Even (1,1,1,1) | demitesseract (16-cell 16-cell In four dimensional geometry, a 16-cell or hexadecachoron is a regular convex 4-polytope. It is one of the six regular convex 4-polytopes first described by the Swiss mathematician Ludwig Schläfli in the mid-19th century.... ) |
||
| [11] | Even (1,1,1,3) | Cantellated demitesseract (cantellated 16-cell) |
||
| [17] | Even (1,1,3,3) | Truncated demitesseract (truncated 16-cell) |
||
| [16] | Even (1,3,3,3) | Cantitruncated demitesseract (cantitruncated 16-cell) |
The grand antiprism
There is one non-Wythoffian uniform convex polychoron, known as the grand antiprismGrand antiprism
In geometry, the grand antiprism or pentagonal double antiprismoid is a uniform polychoron bounded by 320 cells: 20 pentagonal antiprisms, and 300 tetrahedra. It is an anomalous, non-Wythoffian uniform polychoron, discovered in 1965 by Conway and Guy.- Alternate names :* Pentagonal double...
, consisting of 20 pentagonal antiprism
Pentagonal antiprism
In geometry, the pentagonal antiprism is the third in an infinite set of antiprisms formed by an even-numbered sequence of triangle sides closed by two polygon caps. It consists of two pentagons joined to each other by a ring of 10 triangles for a total of 12 faces...
s forming two perpendicular rings joined by 300 tetrahedra
Tetrahedron
In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...
. It is loosely analogous to the three-dimensional antiprism
Antiprism
In geometry, an n-sided antiprism is a polyhedron composed of two parallel copies of some particular n-sided polygon, connected by an alternating band of triangles...
s, which consist of two parallel polygon
Polygon
In geometry a polygon is a flat shape consisting of straight lines that are joined to form a closed chain orcircuit.A polygon is traditionally a plane figure that is bounded by a closed path, composed of a finite sequence of straight line segments...
s joined by a band of triangle
Triangle
A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....
s. Unlike them, however, the grand antiprism is not a member of an infinite family of uniform polytopes.
Its symmetry number is 400 (the ionic diminished Coxeter group).
| # | Johnson Name (Bowers style acronym) | Picture | Vertex figure Vertex figure In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:... |
Coxeter-Dynkin Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... and Schläfli symbols |
Cells by type | Element counts | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| Cells | Faces | Edges | Vertices | |||||||
| 47 | grand antiprism Grand antiprism In geometry, the grand antiprism or pentagonal double antiprismoid is a uniform polychoron bounded by 320 cells: 20 pentagonal antiprisms, and 300 tetrahedra. It is an anomalous, non-Wythoffian uniform polychoron, discovered in 1965 by Conway and Guy.- Alternate names :* Pentagonal double... (gap) |
 |
No symbol | 300 (3.3.3 Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids... )  |
20 (3.3.3.5 Pentagonal antiprism In geometry, the pentagonal antiprism is the third in an infinite set of antiprisms formed by an even-numbered sequence of triangle sides closed by two polygon caps. It consists of two pentagons joined to each other by a ring of 10 triangles for a total of 12 faces... ) 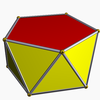 |
320 | 20 {5} Pentagon In geometry, a pentagon is any five-sided polygon. A pentagon may be simple or self-intersecting. The sum of the internal angles in a simple pentagon is 540°. A pentagram is an example of a self-intersecting pentagon.- Regular pentagons :In a regular pentagon, all sides are equal in length and... 700 {3} Triangle A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted .... |
500 | 100 |
Prismatic uniform polychora
A prismatic polytope is a Cartesian productCartesian product
In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
of two polytopes of lower dimension; familiar examples are the 3-dimensional prisms
Prism (geometry)
In geometry, a prism is a polyhedron with an n-sided polygonal base, a translated copy , and n other faces joining corresponding sides of the two bases. All cross-sections parallel to the base faces are the same. Prisms are named for their base, so a prism with a pentagonal base is called a...
, which are products of a polygon
Polygon
In geometry a polygon is a flat shape consisting of straight lines that are joined to form a closed chain orcircuit.A polygon is traditionally a plane figure that is bounded by a closed path, composed of a finite sequence of straight line segments...
and a line segment
Line segment
In geometry, a line segment is a part of a line that is bounded by two end points, and contains every point on the line between its end points. Examples of line segments include the sides of a triangle or square. More generally, when the end points are both vertices of a polygon, the line segment...
. The prismatic uniform polychora consist of two infinite families:
- Polyhedral prisms: products of a line segment and a uniform polyhedron. This family is infinite because it includes prisms built on 3-dimensional prisms and antiprismAntiprismIn geometry, an n-sided antiprism is a polyhedron composed of two parallel copies of some particular n-sided polygon, connected by an alternating band of triangles...
s. - Duoprisms: products of two polygons.
Convex polyhedral prisms
The most obvious family of prismatic polychora is the polyhedral prisms, i.e. products of a polyhedron with a line segmentLine segment
In geometry, a line segment is a part of a line that is bounded by two end points, and contains every point on the line between its end points. Examples of line segments include the sides of a triangle or square. More generally, when the end points are both vertices of a polygon, the line segment...
. The cells of such a polychoron are two identical uniform polyhedra lying in parallel hyperplane
Hyperplane
A hyperplane is a concept in geometry. It is a generalization of the plane into a different number of dimensions.A hyperplane of an n-dimensional space is a flat subset with dimension n − 1...
s (the base cells) and a layer of prisms joining them (the lateral cells). This family includes prisms for the 75 nonprismatic uniform polyhedra
Uniform polyhedron
A uniform polyhedron is a polyhedron which has regular polygons as faces and is vertex-transitive...
(of which 18 are convex; one of these, the cube-prism, is listed above as the tesseract).
There are 18 convex polyhedral prisms created from 5 Platonic solid
Platonic solid
In geometry, a Platonic solid is a convex polyhedron that is regular, in the sense of a regular polygon. Specifically, the faces of a Platonic solid are congruent regular polygons, with the same number of faces meeting at each vertex; thus, all its edges are congruent, as are its vertices and...
s and 13 Archimedean solid
Archimedean solid
In geometry an Archimedean solid is a highly symmetric, semi-regular convex polyhedron composed of two or more types of regular polygons meeting in identical vertices...
s as well as for the infinite families of three-dimensional prism
Prism (geometry)
In geometry, a prism is a polyhedron with an n-sided polygonal base, a translated copy , and n other faces joining corresponding sides of the two bases. All cross-sections parallel to the base faces are the same. Prisms are named for their base, so a prism with a pentagonal base is called a...
s and antiprism
Antiprism
In geometry, an n-sided antiprism is a polyhedron composed of two parallel copies of some particular n-sided polygon, connected by an alternating band of triangles...
s. The symmetry number of a polyhedral prism is twice that of the base polyhedron.
Tetrahedral prisms: A3 × A1
| # | Johnson Name (Bowers style acronym) | Picture | Coxeter-Dynkin Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... and Schläfli symbols |
Cells by type | Element counts | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Cells | Faces | Edges | Vertices | |||||||
| 48 | Tetrahedral prism (tepe) |  |
t0{3,3}×{} |
2  3.3.3 Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids... |
4  3.4.4 Triangular prism In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides.... |
6 | 8 {3} 6 {4} |
16 | 8 | |
| 49 | Truncated tetrahedral prism Truncated tetrahedral prism In geometry, a truncated tetrahedral prism is a convex uniform polychoron . This polychoron has 10 polyhedral cells: 2 truncated tetrahedra connected by 4 triangular prisms and 4 hexagonal prisms. It has 24 faces: 8 triangular, 18 square, and 8 hexagons. It has 48 edges and 24 vertices.Alternative... (tuttip) |
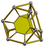 |
t0,1{3,3}×{} |
2  3.6.6 Truncated tetrahedron In geometry, the truncated tetrahedron is an Archimedean solid. It has 4 regular hexagonal faces, 4 regular triangular faces, 12 vertices and 18 edges.- Area and volume :... |
4  3.4.4 Triangular prism In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides.... |
4  4.4.6 Hexagonal prism In geometry, the hexagonal prism is a prism with hexagonal base. The shape has 8 faces, 18 edges, and 12 vertices.Since it has eight faces, it is an octahedron. However, the term octahedron is primarily used to refer to the regular octahedron, which has eight triangular faces... |
10 | 8 {3} 18 {4} 8 {6} |
48 | 24 |
| [51] | Rectified tetrahedral prism (Same as octahedral prism Octahedral prism In geometry, a octahedral prism is a convex uniform polychoron . This polychoron has 10 polyhedral cells: 2 octahedra connected by 8 triangular prisms.- Related polytopes :... ) (ope) |
 |
t1{3,3}×{} |
2  3.3.3.3 Octahedron In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex.... |
4  3.4.4 Triangular prism In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides.... |
6 | 16 {3} 12 {4} |
30 | 12 | |
| [50] | Cantellated tetrahedral prism (Same as cuboctahedral prism Cuboctahedral prism In geometry, a cuboctahedral prism is a convex uniform polychoron . This polychoron has 16 polyhedral cells: 2 cuboctahedra connected by 8 triangular prisms, and 6 cubes.... ) (cope) |
 |
t0,2{3,3}×{} |
2  3.4.3.4 Cuboctahedron In geometry, a cuboctahedron is a polyhedron with eight triangular faces and six square faces. A cuboctahedron has 12 identical vertices, with two triangles and two squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such it is a quasiregular polyhedron,... |
8  3.4.4 Triangular prism In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides.... |
6  4.4.4 Cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and... |
16 | 16 {3} 36 {4} |
60 | 24 |
| [54] | Cantitruncated tetrahedral prism (Same as truncated octahedral prism Truncated octahedral prism In 4-dimensional geometry, a truncated octahedral prism is a convex uniform polychoron . This polychoron has 16 cells It has 64 faces , and 96 edges and 48 vertices.It has two symmetry constructions, one from the truncated octahedron, and one as an omnitruncation of... ) (tope) |
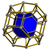 |
t0,1,2{3,3}×{} |
2  4.6.6 Truncated octahedron In geometry, the truncated octahedron is an Archimedean solid. It has 14 faces , 36 edges, and 24 vertices. Since each of its faces has point symmetry the truncated octahedron is a zonohedron.... |
8  6.4.4 Hexagonal prism In geometry, the hexagonal prism is a prism with hexagonal base. The shape has 8 faces, 18 edges, and 12 vertices.Since it has eight faces, it is an octahedron. However, the term octahedron is primarily used to refer to the regular octahedron, which has eight triangular faces... |
6  4.4.4 Cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and... |
16 | 48 {4} 16 {6} |
96 | 48 |
| [59] | Snub tetrahedral prism (Same as icosahedral prism Icosahedral prism In geometry, an icosahedral prism is a convex uniform polychoron . This polychoron has 22 polyhedral cells: 2 icosahedra connected by 20 triangular prisms. It has 70 faces: 30 squares and 40 triangles... ) (ipe) |
 |
s{3,3}×{} |
2  3.3.3.3.3 Icosahedron In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids.... |
20  3.4.4 Triangular prism In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides.... |
22 | 40 {3} 30 {4} |
72 | 24 |
Octahedral prisms: BC3 × A1
| # | Johnson Name (Bowers style acronym) | Picture | Coxeter-Dynkin Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... and Schläfli symbols |
Cells by type | Element counts | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Cells | Faces | Edges | Vertices | ||||||||
| [10] | Cubic prism (Same as tesseract Tesseract In geometry, the tesseract, also called an 8-cell or regular octachoron or cubic prism, is the four-dimensional analog of the cube. The tesseract is to the cube as the cube is to the square. Just as the surface of the cube consists of 6 square faces, the hypersurface of the tesseract consists of 8... ) (Same as 4-4 duoprism) (tes) |
 |
t0{4,3}×{} |
2  4.4.4 Cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and... |
6  4.4.4 Cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and... |
8 | 24 {4} | 32 | 16 | ||
| 50 | Cuboctahedral prism Cuboctahedral prism In geometry, a cuboctahedral prism is a convex uniform polychoron . This polychoron has 16 polyhedral cells: 2 cuboctahedra connected by 8 triangular prisms, and 6 cubes.... (Same as cantellated tetrahedral prism) (cope) |
 |
t1{4,3}×{} |
2  3.4.3.4 Cuboctahedron In geometry, a cuboctahedron is a polyhedron with eight triangular faces and six square faces. A cuboctahedron has 12 identical vertices, with two triangles and two squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such it is a quasiregular polyhedron,... |
8  3.4.4 Triangular prism In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides.... |
6  4.4.4 Cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and... |
16 | 16 {3} 36 {4} |
60 | 24 | |
| 51 | Octahedral prism Octahedral prism In geometry, a octahedral prism is a convex uniform polychoron . This polychoron has 10 polyhedral cells: 2 octahedra connected by 8 triangular prisms.- Related polytopes :... (Same as rectified tetrahedral prism) (Same as triangular antiprismatic prism) (ope) |
 |
t2{4,3}×{} |
2  3.3.3.3 Octahedron In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex.... |
8  3.4.4 Triangular prism In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides.... |
10 | 16 {3} 12 {4} |
30 | 12 | ||
| 52 | Rhombicuboctahedral prism Rhombicuboctahedral prism In geometry, a rhombicuboctahedral prism is a convex uniform polychoron .It is one of 18 convex uniform polyhedral prisms created by using uniform prisms to connect pairs of Platonic solids or Archimedean solids in parallel hyperplanes.- Alternative names :* rhombicuboctahedral dyadic prism In... (sircope) |
 |
t0,2{4,3}×{} |
2  3.4.4.4 Rhombicuboctahedron In geometry, the rhombicuboctahedron, or small rhombicuboctahedron, is an Archimedean solid with eight triangular and eighteen square faces. There are 24 identical vertices, with one triangle and three squares meeting at each. Note that six of the squares only share vertices with the triangles... |
8  3.4.4 Triangular prism In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides.... |
18  4.4.4 Cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and... |
28 | 16 {3} 84 {4} |
120 | 96 | |
| 53 | Truncated cubic prism Truncated cubic prism In geometry, a truncated cubic prism is a convex uniform polychoron .It is one of 18 convex uniform polyhedral prisms created by using uniform prisms to connect pairs of Platonic solids or Archimedean solids in parallel hyperplanes.- Alternative names :* Truncated-cubic hyperprism* Truncated-cubic... (ticcup) |
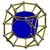 |
t0,1{4,3}×{} |
2  3.8.8 Truncated cube In geometry, the truncated cube, or truncated hexahedron, is an Archimedean solid. It has 14 regular faces , 36 edges, and 24 vertices.... |
8  3.4.4 Triangular prism In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides.... |
6  4.4.8 Octagonal prism In geometry, the octagonal prism is the sixth in an infinite set of prisms, formed by square sides and two regular octagon caps.If faces are all regular, it is a semiregular polyhedron.- Use :... |
16 | 16 {3} 36 {4} 12 {8} |
96 | 48 | |
| 54 | Truncated octahedral prism Truncated octahedral prism In 4-dimensional geometry, a truncated octahedral prism is a convex uniform polychoron . This polychoron has 16 cells It has 64 faces , and 96 edges and 48 vertices.It has two symmetry constructions, one from the truncated octahedron, and one as an omnitruncation of... (Same as cantitruncated tetrahedral prism) (tope) |
 |
t1,2{4,3}×{} |
2  4.6.6 Truncated octahedron In geometry, the truncated octahedron is an Archimedean solid. It has 14 faces , 36 edges, and 24 vertices. Since each of its faces has point symmetry the truncated octahedron is a zonohedron.... |
6  4.4.4 Cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and... |
8  4.4.6 Hexagonal prism In geometry, the hexagonal prism is a prism with hexagonal base. The shape has 8 faces, 18 edges, and 12 vertices.Since it has eight faces, it is an octahedron. However, the term octahedron is primarily used to refer to the regular octahedron, which has eight triangular faces... |
16 | 48 {4} 16 {6} |
96 | 48 | |
| 55 | Truncated cuboctahedral prism Truncated cuboctahedral prism In geometry, a truncated cuboctahedral prism is a convex uniform polychoron .It is one of 18 convex uniform polyhedral prisms created by using uniform prisms to connect pairs of Platonic solids or Archimedean solids in parallel hyperplanes.- Alternative names :* Truncated-cuboctahedral dyadic prism... (gircope) |
 |
t0,1,2{4,3}×{} |
2  4.6.8 Truncated cuboctahedron In geometry, the truncated cuboctahedron is an Archimedean solid. It has 12 square faces, 8 regular hexagonal faces, 6 regular octagonal faces, 48 vertices and 72 edges... |
12  4.4.4 Cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and... |
8  4.4.6 Hexagonal prism In geometry, the hexagonal prism is a prism with hexagonal base. The shape has 8 faces, 18 edges, and 12 vertices.Since it has eight faces, it is an octahedron. However, the term octahedron is primarily used to refer to the regular octahedron, which has eight triangular faces... |
6  4.4.8 Octagonal prism In geometry, the octagonal prism is the sixth in an infinite set of prisms, formed by square sides and two regular octagon caps.If faces are all regular, it is a semiregular polyhedron.- Use :... |
28 | 96 {4} 16 {6} 12 {8} |
192 | 96 |
| 56 | Snub cubic prism Snub cubic prism In geometry, a truncated cuboctahedral prism is a convex uniform polychoron .It is one of 18 convex uniform polyhedral prisms created by using uniform prisms to connect pairs of Platonic solids or Archimedean solids in parallel hyperplanes.- Alternative names :* Snub-cuboctahedral dyadic prism In... (sniccup) |
 |
s{4,3}×{} |
2  3.3.3.3.4 Snub cube In geometry, the snub cube, or snub cuboctahedron, is an Archimedean solid.The snub cube has 38 faces, 6 of which are squares and the other 32 are equilateral triangles. It has 60 edges and 24 vertices. It is a chiral polyhedron, that is, it has two distinct forms, which are mirror images of each... |
32  3.4.4 Triangular prism In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides.... |
6  4.4.4 Cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and... |
40 | 64 {3} 72 {4} |
144 | 48 |
Icosahedral prisms: H3 × A1
| # | Johnson Name (Bowers style acronym) | Picture | Coxeter-Dynkin Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... and Schläfli symbols |
Cells by type | Element counts | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Cells | Faces | Edges | Vertices | ||||||||
| 57 | Dodecahedral prism (dope) | 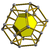 |
t0{5,3}×{} |
2  5.5.5 |
12  4.4.5 Pentagonal prism In geometry, the pentagonal prism is a prism with a pentagonal base. It is a type of heptahedron with 7 faces, 15 edges, and 10 vertices.- As a semiregular polyhedron :... |
14 | 30 {4} 24 {5} |
80 | 40 | ||
| 58 | Icosidodecahedral prism Icosidodecahedral prism In geometry, an icosidodecahedral prism is a convex uniform polychoron .It is one of 18 convex uniform polyhedral prisms created by using uniform prisms to connect pairs of parallel Platonic solids or Archimedean solids.... (iddip) |
 |
t1{5,3}×{} |
2  3.5.3.5 Icosidodecahedron In geometry, an icosidodecahedron is a polyhedron with twenty triangular faces and twelve pentagonal faces. An icosidodecahedron has 30 identical vertices, with two triangles and two pentagons meeting at each, and 60 identical edges, each separating a triangle from a pentagon... |
20  3.4.4 Triangular prism In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides.... |
12  4.4.5 Pentagonal prism In geometry, the pentagonal prism is a prism with a pentagonal base. It is a type of heptahedron with 7 faces, 15 edges, and 10 vertices.- As a semiregular polyhedron :... |
34 | 40 {3} 60 {4} 24 {5} |
150 | 60 | |
| 59 | Icosahedral prism Icosahedral prism In geometry, an icosahedral prism is a convex uniform polychoron . This polychoron has 22 polyhedral cells: 2 icosahedra connected by 20 triangular prisms. It has 70 faces: 30 squares and 40 triangles... (same as snub tetrahedral prism) (ipe) |
 |
t2{5,3}×{} |
2  3.3.3.3.3 Icosahedron In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids.... |
20  3.4.4 Triangular prism In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides.... |
22 | 40 {3} 30 {4} |
72 | 24 | ||
| 60 | Truncated dodecahedral prism Truncated dodecahedral prism In geometry, a truncated dodecahedral prism is a convex uniform polychoron .It is one of 18 convex uniform polyhedral prisms created by using uniform prisms to connect pairs of Platonic solids or Archimedean solids in parallel hyperplanes.- Alternative names :* Truncated-dodecahedral dyadic prism... (tiddip) |
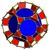 |
t0,1{5,3}×{} |
2  3.10.10 Truncated dodecahedron In geometry, the truncated dodecahedron is an Archimedean solid. It has 12 regular decagonal faces, 20 regular triangular faces, 60 vertices and 90 edges.- Geometric relations :... |
20  3.4.4 Triangular prism In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides.... |
12  4.4.5 Decagonal prism In geometry, the decagonal prism is the eighth in an infinite set of prisms, formed by ten square side faces and two regular decagon caps. With twelve faces, it is one of many nonregular dodecahedra.If faces are all regular, it is a semiregular polyhedron.... |
34 | 40 {3} 90 {4} 24 {10} |
240 | 120 | |
| 61 | Rhombicosidodecahedral prism Rhombicosidodecahedral prism In geometry, a rhombicosidodecahedral prism is a convex uniform polychoron .It is one of 18 convex uniform polyhedral prisms created by using uniform prisms to connect pairs of Platonic solids or Archimedean solids in parallel hyperplanes.- Alternative names :* rhombicosidodecahedral dyadic prism... (sriddip) |
 |
t0,2{5,3}×{} |
2  3.4.5.4 Rhombicosidodecahedron In geometry, the rhombicosidodecahedron, or small rhombicosidodecahedron, is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids constructed of two or more types of regular polygon faces.... |
20  3.4.4 Triangular prism In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides.... |
30  4.4.4 Cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and... |
12  4.4.5 Pentagonal prism In geometry, the pentagonal prism is a prism with a pentagonal base. It is a type of heptahedron with 7 faces, 15 edges, and 10 vertices.- As a semiregular polyhedron :... |
64 | 40 {3} 180 {4} 24 {5} |
300 | 120 |
| 62 | Truncated icosahedral prism Truncated icosahedral prism In geometry, a truncated icosahedral prism is a convex uniform polychoron .It is one of 18 convex uniform polyhedral prisms created by using uniform prisms to connect pairs of Platonic solids or Archimedean solids in parallel hyperplanes.- Alternative names :* Truncated-icosahedral dyadic prism In... (tipe) |
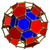 |
t1,2{5,3}×{} |
2  5.6.6 Truncated icosahedron In geometry, the truncated icosahedron is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids whose faces are two or more types of regular polygons.It has 12 regular pentagonal faces, 20 regular hexagonal faces, 60 vertices and 90 edges.... |
12  4.4.5 Pentagonal prism In geometry, the pentagonal prism is a prism with a pentagonal base. It is a type of heptahedron with 7 faces, 15 edges, and 10 vertices.- As a semiregular polyhedron :... |
20  4.4.6 Hexagonal prism In geometry, the hexagonal prism is a prism with hexagonal base. The shape has 8 faces, 18 edges, and 12 vertices.Since it has eight faces, it is an octahedron. However, the term octahedron is primarily used to refer to the regular octahedron, which has eight triangular faces... |
34 | 90 {4} 24 {5} 40 {6} |
240 | 120 | |
| 63 | Truncated icosidodecahedral prism Truncated icosidodecahedral prism In geometry, a truncated icosidodecahedral prism is a convex uniform polychoron .It is one of 18 convex uniform polyhedral prisms created by using uniform prisms to connect pairs of Platonic solids or Archimedean solids in parallel hyperplanes.- Alternative names :* Truncated-icosidodecahedral... (griddip) |
 |
t0,1,2{5,3}×{} |
2  4.6.4.10 Truncated icosidodecahedron In geometry, the truncated icosidodecahedron is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids constructed by two or more types of regular polygon faces.... |
30  4.4.4 Cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and... |
20  4.4.6 Hexagonal prism In geometry, the hexagonal prism is a prism with hexagonal base. The shape has 8 faces, 18 edges, and 12 vertices.Since it has eight faces, it is an octahedron. However, the term octahedron is primarily used to refer to the regular octahedron, which has eight triangular faces... |
12  4.4.10 Decagonal prism In geometry, the decagonal prism is the eighth in an infinite set of prisms, formed by ten square side faces and two regular decagon caps. With twelve faces, it is one of many nonregular dodecahedra.If faces are all regular, it is a semiregular polyhedron.... |
64 | 240 {4} 40 {6} 24 {5} |
480 | 240 |
| 64 | Snub dodecahedral prism Snub dodecahedral prism In geometry, a snub dodecahedral prism is a convex uniform polychoron .It is one of 18 convex uniform polyhedral prisms created by using uniform prisms to connect pairs of Platonic solids or Archimedean solids in parallel hyperplanes.- Alternative names :* Snub-icosidodecahedral dyadic prism In... (sniddip) |
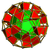 |
s{5,3}×{} |
2  3.3.3.3.5 Snub dodecahedron In geometry, the snub dodecahedron, or snub icosidodecahedron, is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids constructed by two or more types of regular polygon faces.... |
80  3.4.4 Triangular prism In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides.... |
12  4.4.5 Pentagonal prism In geometry, the pentagonal prism is a prism with a pentagonal base. It is a type of heptahedron with 7 faces, 15 edges, and 10 vertices.- As a semiregular polyhedron :... |
94 | 240 {4} 40 {6} 24 {10} |
360 | 120 |
Duoprisms: [p] × [q]
Duoprism
In geometry of 4 dimensions or higher, a duoprism is a polytope resulting from the Cartesian product of two polytopes, each of two dimensions or higher...
, products of two regular polygon
Regular polygon
A regular polygon is a polygon that is equiangular and equilateral . Regular polygons may be convex or star.-General properties:...
s.
Their Coxeter-Dynkin diagram
Coxeter-Dynkin diagram
In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors...
is of the form
This family overlaps with the first: when one of the two "factor" polygons is a square, the product is equivalent to a hyperprism whose base is a three-dimensional prism. The symmetry number of a duoprism whose factors are a p-gon and a q-gon (a "p,q-duoprism") is 4pq if p≠q; if the factors are both p-gons, the symmetry number is 8p2. The tesseract can also be considered a 4,4-duoprism.
The elements of a p,q-duoprism (p ≥ 3, q ≥ 3) are:
- Cells: p q-gonal prisms, q p-gonal prisms
- Faces: pq squares, p q-gons, q p-gons
- Edges: 2pq
- Vertices: pq
There is no uniform analogue in four dimensions to the infinite family of three-dimensional antiprism
Antiprism
In geometry, an n-sided antiprism is a polyhedron composed of two parallel copies of some particular n-sided polygon, connected by an alternating band of triangles...
s.
Infinite set of p-q duoprism - - p q-gonal prisms, q p-gonal prisms:
- 3-3 duoprism - - 6 triangular prisms
- 3-4 duoprism - - 3 cubes, 4 triangular prisms
- 4-4 duoprism - - 8 cubes (same as tesseract)
- 3-5 duoprism - - 3 pentagonal prisms, 5 triangular prisms
- 4-5 duoprism - - 4 pentagonal prisms, 5 cubes
- 5-5 duoprism - - 10 pentagonal prisms
- 3-6 duoprism - - 3 hexagonal prisms, 6 triangular prisms
- 4-6 duoprism - - 4 hexagonal prisms, 6 cubes
- 5-6 duoprism - - 5 hexagonal prisms, 6 pentagonal prisms
- 6-6 duoprism - - 12 hexagonal prisms
- ...
Polygonal prismatic prisms: [p] × [ ] × [ ]
The infinte set of uniform prismatic prisms overlaps with the 4-p duoprisms: (p≥3) - - p cubes and 4 p-gonal prisms - (All are the same as 4-p duoprism)- Triangular prismatic prism - - 3 cubes and 4 triangular prisms - (same as 3-4 duoprism)
- Square prismatic prism - - 4 cubes and 4 cubes - (same as 4-4 duoprism and same as tesseract)
- Pentagonal prismatic prism - - 5 cubes and 4 pentagonal prisms - (same as 4-5 duoprism)
- Hexagonal prismatic prism - - 6 cubes and 4 hexagonal prisms - (same as 4-6 duoprism)
- Heptagonal prismatic prism - - 7 cubes and 4 heptagonal prisms - (same as 4-7 duoprism)
- Octagonal prismatic prism - - 8 cubes and 4 octagonal prisms - (same as 4-8 duoprism)
- ...
The infinite sets of uniform antiprismatic prism
Uniform antiprismatic prism
In 4-dimensional geometry, a uniform antiprismatic prism is a uniform polychoron with two uniform antiprism cells in two parallel 3-space hyperplanes, connected by uniform prisms cells between pairs of faces....
s are constructed from two parallel uniform antiprism
Antiprism
In geometry, an n-sided antiprism is a polyhedron composed of two parallel copies of some particular n-sided polygon, connected by an alternating band of triangles...
s): (p≥3) - - 2 p-gonal antiprisms, connected by 2 p-gonal prisms and 2p triangular prisms.
- Triangular antiprismatic prism - - 2 octahedras connected by 8 triangular prismTriangular prismIn geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides....
s (same as the octahedral prism) - Square antiprismatic prismSquare antiprismatic prismIn geometry, a square antiprismatic prism is a convex uniform polychoron . It is formed as two parallel square antiprisms connected by cubes and triangular prisms.- Related polytopes :...
- - 2 square antiprismSquare antiprismIn geometry, the square antiprism is the second in an infinite set of antiprisms formed by an even-numbered sequence of triangle sides closed by two polygon caps...
s connected by 2 cubes and 8 triangular prismTriangular prismIn geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides....
s
- Pentagonal antiprismatic prism - - 2 pentagonal antiprismPentagonal antiprismIn geometry, the pentagonal antiprism is the third in an infinite set of antiprisms formed by an even-numbered sequence of triangle sides closed by two polygon caps. It consists of two pentagons joined to each other by a ring of 10 triangles for a total of 12 faces...
s connected by 2 pentagonal prisms and 10 triangular prismTriangular prismIn geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides....
s
- Hexagonal antiprismatic prism - - 2 hexagonal antiprismHexagonal antiprismIn geometry, the hexagonal antiprism is the 4th in an infinite set of antiprisms formed by an even-numbered sequence of triangle sides closed by two polygon caps.If faces are all regular, it is a semiregular polyhedron.- See also :* Set of antiprisms...
s connected by 2 hexagonal prisms and 12 triangular prismTriangular prismIn geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides....
s - Heptagonal antiprismatic prism - - 2 heptagonal antiprismHeptagonal antiprismIn geometry, the heptagonal antiprism is the fourth in an infinite set of antiprisms formed by an even-numbered sequence of triangle sides closed by two polygon caps.If faces are all regular, it is a semiregular polyhedron.- See also :* Set of antiprisms...
s connected by 2 heptagonal prisms and 14 triangular prismTriangular prismIn geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides....
s - Octagonal antiprismatic prism - - 2 octagonal antiprismOctagonal antiprismIn geometry, the octagonal antiprism is the 6th in an infinite set of antiprisms formed by an even-numbered sequence of triangle sides closed by two polygon caps.If faces are all regular, it is a semiregular polyhedron.- See also :* Set of antiprisms...
s connected by 2 octagonal prisms and 16 triangular prismTriangular prismIn geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides....
s - ...
A p-gonal antiprismatic prism has 4p triangle, 4p square and 4 p-gon faces. It has 10p edges, and 4p vertices.
Geometric derivations for 46 nonprismatic Wythoffian uniform polychora
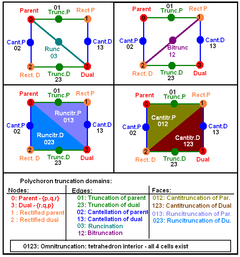

Convex regular 4-polytope
In mathematics, a convex regular 4-polytope is a 4-dimensional polytope that is both regular and convex. These are the four-dimensional analogs of the Platonic solids and the regular polygons ....
. The other forty can be derived from the regular polychora by geometric operations which preserve most or all of their symmetries
Symmetry
Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...
, and therefore may be classified by the symmetry group
Symmetry group
The symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation...
s that they have in common.
The geometric operations that derive the 40 uniform polychora from the regular polychora are truncating operations. A polychoron may be truncated at the vertices, edges or faces, leading to addition of cells corresponding to those elements, as shown in the columns of the tables below.
The Coxeter-Dynkin diagram
Coxeter-Dynkin diagram
In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors...
shows the four mirrors of the Wythoffian kaleidoscope as nodes, and the edges between the nodes are labeled by an integer showing the angle between the mirrors (π
Pi
' is a mathematical constant that is the ratio of any circle's circumference to its diameter. is approximately equal to 3.14. Many formulae in mathematics, science, and engineering involve , which makes it one of the most important mathematical constants...
/n radian
Radian
Radian is the ratio between the length of an arc and its radius. The radian is the standard unit of angular measure, used in many areas of mathematics. The unit was formerly a SI supplementary unit, but this category was abolished in 1995 and the radian is now considered a SI derived unit...
s or 180/n degrees). Circled nodes show which mirrors are active for each form; a mirror is active with respect to a vertex that does not lie on it.
| Operation | Schläfli symbol |
Coxeter- Dynkin diagram Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... |
Description |
|---|---|---|---|
| Parent | t0{p,q,r} | Original regular form {p,q,r} | |
| Rectification Rectification (geometry) In Euclidean geometry, rectification is the process of truncating a polytope by marking the midpoints of all its edges, and cutting off its vertices at those points... |
t1{p,q,r} | Truncation operation applied until the original edges are degenerated into points. | |
| Birectification | t2{p,q,r} | Face are fully truncated to points. Same as rectified dual. | |
| Trirectification (dual) |
t3{p,q,r} | Cells are truncated to points. Regular dual {r,q,p} | |
| Truncation Truncation (geometry) In geometry, a truncation is an operation in any dimension that cuts polytope vertices, creating a new facet in place of each vertex.- Uniform truncation :... |
t0,1{p,q,r} | Each vertex is cut off so that the middle of each original edge remains. Where the vertex was, there appears a new cell, the parent's vertex figure Vertex figure In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:... . Each original cell is likewise truncated. |
|
| Bitruncation | t1,2{p,q,r} | A truncation between a rectified form and the dual rectified form. | |
| Tritruncation | t2,3{p,q,r} | Truncated dual {r,q,p}. | |
| Cantellation Cantellation (geometry) In geometry, a cantellation is an operation in any dimension that cuts a regular polytope at its edges and vertices, creating a new facet in place of each edge and vertex. The operation also applies to regular tilings and honeycombs... |
t0,2{p,q,r} | A truncation applied to edges and vertices and defines a progression between the regular and dual rectified form. | |
| Bicantellation | t1,3{p,q,r} | Cantellated dual {r,q,p}. | |
| Runcination (or expansion Expansion (geometry) In geometry, expansion is a polytope operation where facets are separated and moved radially apart, and new facets are formed at separated elements... ) |
t0,3{p,q,r} | A truncation applied to the cells, faces and edges; defines a progression between a regular form and the dual. | |
| Cantitruncation | t0,1,2{p,q,r} | Both the cantellation and truncation operations applied together. | |
| Bicantitruncation | t1,2,3{p,q,r} | Cantitruncated dual {r,q,p}. | |
| Runcitruncation | t0,1,3{p,q,r} | Both the runcination and truncation operations applied together. | |
| Runcicantellation | t0,1,3{p,q,r} | Runcitruncated dual {r,q,p}. | |
| Omnitruncation Omnitruncation (geometry) In geometry, an omnitruncation is an operation applied to a regular polytope in a Wythoff construction that creates a maximum number of facets... (or more specifically runcicantitruncation) |
t0,1,2,3{p,q,r} | Application of all three operators. | |
| Snub Snub (geometry) In geometry, an alternation is an operation on a polyhedron or tiling that removes alternate vertices. Only even-sided polyhedra can be alternated, for example the zonohedra. Every 2n-sided face becomes n-sided... |
s{p,q,r} | An alternation of an omnitruncated form. (Rings are replaced by holes.) |
See also convex uniform honeycomb
Convex uniform honeycomb
In geometry, a convex uniform honeycomb is a uniform tessellation which fills three-dimensional Euclidean space with non-overlapping convex uniform polyhedral cells.Twenty-eight such honeycombs exist:* the familiar cubic honeycomb and 7 truncations thereof;...
s, some of which illustrate these operations as applied to the regular cubic honeycomb
Cubic honeycomb
The cubic honeycomb is the only regular space-filling tessellation in Euclidean 3-space, made up of cubic cells. It has 4 cubes around every edge, and 8 cubes around each vertex. Its vertex figure is a regular octahedron....
.
If two polytopes are duals of each other (such as the tesseract and 16-cell, or the 120-cell and 600-cell), then bitruncating, runcinating or omnitruncating either produces the same figure as the same operation to the other. Thus where only the participle appears in the table it should be understood to apply to either parent.
External links
- Convex uniform polychora
- uniform, convex polytopes in four dimensions:, Marco Möller
}
- Nonconvex uniform polychora
- Uniform polychora by Jonathan Bowers
- Stella4D Stella (software)Stella (software)Stella, a computer program available in three versions was created by Robert Webb of Australia...
produces interactive views of all 1849 known uniform polychora including the 64 convex forms and the infinite prismatic families. Was used to create most images on this page.

