
16-cell
Encyclopedia
In four dimensional geometry
, a 16-cell or hexadecachoron is a regular convex 4-polytope. It is one of the six regular convex 4-polytopes first described by the Swiss mathematician Ludwig Schläfli
in the mid-19th century.
It is a part of an infinite family of polytopes, called cross-polytope
s or orthoplexes. The dual polytope is the tesseract
(4-cube
). Conway
's name for a cross-polytope is orthoplex, for orthant
complex.
. It has 32 triangular faces, 24 edges, and 8 vertices. The 24 edges bound 6 squares lying in the 6 coordinate planes.
The eight vertices of the 16-cell are (±1, 0, 0, 0), (0, ±1, 0, 0), (0, 0, ±1, 0), (0, 0, 0, ±1). All vertices are connected by edges except opposite pairs.
The Schläfli symbol of the 16-cell is {3,3,4}. Its vertex figure
is a regular octahedron. There are 8 tetrahedra, 12 triangles, and 6 edges meeting at every vertex. Its edge figure is a square. There are 4 tetrahedra and 4 triangles meeting at every edge.
There is a lower symmetry form of the 16-cell, called a demitesseract or 4-demicube, a member of the demihypercube family, and represented by h{4,3,3}, and Coxeter diagrams or . It can be drawn bicolored with alternating tetrahedral
cells.
It can also be seen in lower symmetry form as a tetrahedral antiprism, constructed by 2 parallel tetrahedra
in dual configurations, connected by 8 (possibly elongated) tetrahedra. It is represented by h0,1{2,4,3}, and Coxeter diagram: .
It can also be seen as a snub 4-orthotope, represented by s{2,2,2}, and Coxeter diagram: .
4-dimensional Euclidean space
by regular 16-cells. This is called the hexadecachoric honeycomb and has Schläfli symbol {3,3,4,3}. The dual tessellation, icositetrachoric honeycomb, {3,4,3,3}, is made of by regular 24-cells. Together with the tesseractic honeycomb {4,3,3,4}, these are the only three regular tessellations of R4. Each 16-cell has 16 neighbors with which it shares an octahedron, 24 neighbors with which it shares only an edge, and 72 neighbors with which it shares only a single point. Twenty-four 16-cells meet at any given vertex in this tessellation.
 The cell-first parallel projection of the 16-cell into 3-space has a cubical
The cell-first parallel projection of the 16-cell into 3-space has a cubical
envelope. The closest and farthest cells are projected to inscribed tetrahedra within the cube, corresponding with the two possible ways to inscribe a regular tetrahedron in a cube. Surrounding each of these tetrahedra are 4 other (non-regular) tetrahedral volumes that are the images of the 4 surrounding tetrahedral cells, filling up the space between the inscribed tetrahedron and the cube. The remaining 6 cells are projected onto the square faces of the cube. In this projection of the 16-cell, all its edges lie on the faces of the cubical envelope.
The cell-first perspective projection of the 16-cell into 3-space has a triakis tetrahedral
envelope. The layout of the cells within this envelope are analogous to that of the cell-first parallel projection.
The vertex-first parallel projection
of the 16-cell into 3-space has an octahedral
envelope. This octahedron can be divided into 8 tetrahedral volumes, by cutting along the coordinate planes. Each of these volumes is the image of a pair of cells in the 16-cell. The closest vertex of the 16-cell to the viewer projects onto the center of the octahedron.
Finally the edge-first parallel projection has a shortened octahedral envelope, and the face-first parallel projection has a hexagonal bipyramid
al envelope.
 and 4 intersecting spheres (a Venn diagram
and 4 intersecting spheres (a Venn diagram
of 4 sets) form topologically
the same object in 3D-space:
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, a 16-cell or hexadecachoron is a regular convex 4-polytope. It is one of the six regular convex 4-polytopes first described by the Swiss mathematician Ludwig Schläfli
Ludwig Schläfli
Ludwig Schläfli was a Swiss geometer and complex analyst who was one of the key figures in developing the notion of higher dimensional spaces. The concept of multidimensionality has since come to play a pivotal role in physics, and is a common element in science fiction...
in the mid-19th century.
It is a part of an infinite family of polytopes, called cross-polytope
Cross-polytope
In geometry, a cross-polytope, orthoplex, hyperoctahedron, or cocube is a regular, convex polytope that exists in any number of dimensions. The vertices of a cross-polytope are all the permutations of . The cross-polytope is the convex hull of its vertices...
s or orthoplexes. The dual polytope is the tesseract
Tesseract
In geometry, the tesseract, also called an 8-cell or regular octachoron or cubic prism, is the four-dimensional analog of the cube. The tesseract is to the cube as the cube is to the square. Just as the surface of the cube consists of 6 square faces, the hypersurface of the tesseract consists of 8...
(4-cube
Hypercube
In geometry, a hypercube is an n-dimensional analogue of a square and a cube . It is a closed, compact, convex figure whose 1-skeleton consists of groups of opposite parallel line segments aligned in each of the space's dimensions, perpendicular to each other and of the same length.An...
). Conway
John Horton Conway
John Horton Conway is a prolific mathematician active in the theory of finite groups, knot theory, number theory, combinatorial game theory and coding theory...
's name for a cross-polytope is orthoplex, for orthant
Orthant
In geometry, an orthant or hyperoctant is the analogue in n-dimensional Euclidean space of a quadrant in the plane or an octant in three dimensions....
complex.
Geometry
It is bounded by 16 cells, all of which are regular tetrahedraTetrahedron
In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...
. It has 32 triangular faces, 24 edges, and 8 vertices. The 24 edges bound 6 squares lying in the 6 coordinate planes.
The eight vertices of the 16-cell are (±1, 0, 0, 0), (0, ±1, 0, 0), (0, 0, ±1, 0), (0, 0, 0, ±1). All vertices are connected by edges except opposite pairs.
The Schläfli symbol of the 16-cell is {3,3,4}. Its vertex figure
Vertex figure
In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...
is a regular octahedron. There are 8 tetrahedra, 12 triangles, and 6 edges meeting at every vertex. Its edge figure is a square. There are 4 tetrahedra and 4 triangles meeting at every edge.
There is a lower symmetry form of the 16-cell, called a demitesseract or 4-demicube, a member of the demihypercube family, and represented by h{4,3,3}, and Coxeter diagrams or . It can be drawn bicolored with alternating tetrahedral
Tetrahedron
In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...
cells.
It can also be seen in lower symmetry form as a tetrahedral antiprism, constructed by 2 parallel tetrahedra
Tetrahedron
In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...
in dual configurations, connected by 8 (possibly elongated) tetrahedra. It is represented by h0,1{2,4,3}, and Coxeter diagram: .
It can also be seen as a snub 4-orthotope, represented by s{2,2,2}, and Coxeter diagram: .
Images
 Stereographic projection Stereographic projection The stereographic projection, in geometry, is a particular mapping that projects a sphere onto a plane. The projection is defined on the entire sphere, except at one point — the projection point. Where it is defined, the mapping is smooth and bijective. It is conformal, meaning that it... |
 A 3D projection of a 16-cell performing a simple rotation. |
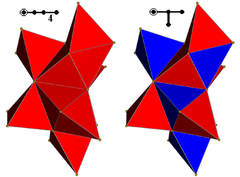 The 16-cell has two Wythoff constructions, a regular form and alternated form, shown here as nets Net (polyhedron) In geometry the net of a polyhedron is an arrangement of edge-joined polygons in the plane which can be folded to become the faces of the polyhedron... , the second being represented by alternately two colors of tetrahedral cells. |
demitesseract in order-4 Petrie polygon symmetry as an alternated tesseract |
 Tesseract Tesseract In geometry, the tesseract, also called an 8-cell or regular octachoron or cubic prism, is the four-dimensional analog of the cube. The tesseract is to the cube as the cube is to the square. Just as the surface of the cube consists of 6 square faces, the hypersurface of the tesseract consists of 8... |
Tessellations
One can tessellateTessellation
A tessellation or tiling of the plane is a pattern of plane figures that fills the plane with no overlaps and no gaps. One may also speak of tessellations of parts of the plane or of other surfaces. Generalizations to higher dimensions are also possible. Tessellations frequently appeared in the art...
4-dimensional Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
by regular 16-cells. This is called the hexadecachoric honeycomb and has Schläfli symbol {3,3,4,3}. The dual tessellation, icositetrachoric honeycomb, {3,4,3,3}, is made of by regular 24-cells. Together with the tesseractic honeycomb {4,3,3,4}, these are the only three regular tessellations of R4. Each 16-cell has 16 neighbors with which it shares an octahedron, 24 neighbors with which it shares only an edge, and 72 neighbors with which it shares only a single point. Twenty-four 16-cells meet at any given vertex in this tessellation.
Projections

Cube
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and...
envelope. The closest and farthest cells are projected to inscribed tetrahedra within the cube, corresponding with the two possible ways to inscribe a regular tetrahedron in a cube. Surrounding each of these tetrahedra are 4 other (non-regular) tetrahedral volumes that are the images of the 4 surrounding tetrahedral cells, filling up the space between the inscribed tetrahedron and the cube. The remaining 6 cells are projected onto the square faces of the cube. In this projection of the 16-cell, all its edges lie on the faces of the cubical envelope.
The cell-first perspective projection of the 16-cell into 3-space has a triakis tetrahedral
Triakis tetrahedron
In geometry, a triakis tetrahedron is an Archimedean dual solid, or a Catalan solid. Its dual is the truncated tetrahedron.It can be seen as a tetrahedron with triangular pyramids added to each face; that is, it is the Kleetope of the tetrahedron...
envelope. The layout of the cells within this envelope are analogous to that of the cell-first parallel projection.
The vertex-first parallel projection
Graphical projection
Graphical projection is a protocol by which an image of a three-dimensional object is projected onto a planar surface without the aid of mathematical calculation, used in technical drawing.- Overview :...
of the 16-cell into 3-space has an octahedral
Octahedron
In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....
envelope. This octahedron can be divided into 8 tetrahedral volumes, by cutting along the coordinate planes. Each of these volumes is the image of a pair of cells in the 16-cell. The closest vertex of the 16-cell to the viewer projects onto the center of the octahedron.
Finally the edge-first parallel projection has a shortened octahedral envelope, and the face-first parallel projection has a hexagonal bipyramid
Hexagonal bipyramid
A hexagonal bipyramid is a polyhedron formed from two hexagonal pyramids joined at their bases. The resulting solid has 12 triangular faces, 8 vertices and 18 edges. The 12 faces are identical isosceles triangles.It is one of an infinite set of bipyramids...
al envelope.
4 sphere Venn Diagram
The usual projection of the 16-cell and 4 intersecting spheres (a Venn diagram
and 4 intersecting spheres (a Venn diagramVenn diagram
Venn diagrams or set diagrams are diagrams that show all possible logical relations between a finite collection of sets . Venn diagrams were conceived around 1880 by John Venn...
of 4 sets) form topologically
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
the same object in 3D-space:
External links
-
- Der 16-Zeller (16-cell) Marco Möller's Regular polytopes in R4 (German)
- Description and diagrams of 16-cell projections

