5-cell	Cantellated 5-cell	Cantitruncated 5-cell
Orthogonal projections in A4 Coxeter plane

In four-dimensional geometry

Geometry

Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....

, a cantellated 5-cell is a convex uniform polychoron

Uniform polychoron

In geometry, a uniform polychoron is a polychoron or 4-polytope which is vertex-transitive and whose cells are uniform polyhedra....

, being a cantellation (a 2nd order truncation) of the regular 5-cell.

There are 2 unique degrees of runcinations of the 5-cell including with permutations truncations.

Cantellation 5-cell

Cantellated 5-cell
Schlegel diagram with octahedral cells shown
Type	Uniform polychoron Uniform polychoron In geometry, a uniform polychoron is a polychoron or 4-polytope which is vertex-transitive and whose cells are uniform polyhedra....
Schläfli symbol	t0,2{3,3,3}
Coxeter-Dynkin diagram Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors...
Cells	20	5 (3.4.3.4) Cuboctahedron In geometry, a cuboctahedron is a polyhedron with eight triangular faces and six square faces. A cuboctahedron has 12 identical vertices, with two triangles and two squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such it is a quasiregular polyhedron,... 5 (3.3.3.3) Octahedron In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex.... 10 (3.4.4) Triangular prism In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides....
Faces	80	50{3} Triangle A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted .... 30{4} Square (geometry) In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles...
Edges	90
Vertices	30
Vertex figure Vertex figure In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...	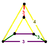Irreg. triangular prism Triangular prism In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides....
Symmetry group Coxeter group In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example...	A4, [3,3,3], order 120
Properties	convex Convex polytope A convex polytope is a special case of a polytope, having the additional property that it is also a convex set of points in the n-dimensional space Rn... , isogonal
Uniform index	3 Truncated 5-cell In geometry, a truncated 5-cell is a uniform polychoron formed as the truncation of the regular 5-cell.There are two degrees of trunctions, including a bitruncation.- Truncated 5-cell:... 4 5

The cantellated

Cantellation (geometry)

In geometry, a cantellation is an operation in any dimension that cuts a regular polytope at its edges and vertices, creating a new facet in place of each edge and vertex. The operation also applies to regular tilings and honeycombs...

 5-cell is a uniform polychoron

Uniform polychoron

In geometry, a uniform polychoron is a polychoron or 4-polytope which is vertex-transitive and whose cells are uniform polyhedra....

. It has 30 vertices, 90 edges, 80 faces, and 20 cells. The cells are 5 cuboctahedra

Cuboctahedron

In geometry, a cuboctahedron is a polyhedron with eight triangular faces and six square faces. A cuboctahedron has 12 identical vertices, with two triangles and two squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such it is a quasiregular polyhedron,...

, 5 octahedra

Octahedron

In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....

, and 10 triangular prism

Triangular prism

In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides....

s. Each vertex is surrounded by 2 cuboctahedra, 2 triangular prisms, and 1 octahedron; the vertex figure

Vertex figure

In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...

 is a nonuniform triangular prism.

Alternate names

• Cantellated pentachoron
• Cantellated 4-simplex
  Simplex
  In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...
  
  
• (small) prismatodispentachoron
• Rectified dispentachoron
• Small rhombated pentachoron (Acronym: Srip) (Jonathan Bowers)

Images

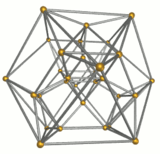Wireframe

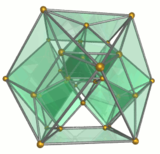Ten triangular prism Triangular prism In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides.... s colored green

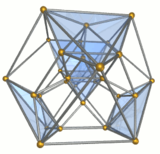Five octahedra colored blue

Coordinates

The Cartesian coordinates of the vertices of the origin-centered cantellated 5-cell having edge length 2 are:


The vertices of the cantellated 5-cell can be most simply positioned in 5-space as permutations of:

(0,0,1,1,2)

This construction is from the positive orthant

Orthant

In geometry, an orthant or hyperoctant is the analogue in n-dimensional Euclidean space of a quadrant in the plane or an octant in three dimensions....

 facet of the cantellated 5-orthoplex

Cantellated 5-orthoplex

In six-dimensional geometry, a cantellated 5-orthoplex is a convex uniform 5-polytope, being a cantellation of the regular 5-orthoplex.There are 6 cantellation for the 5-orthoplex, including truncations...

.

Cantitruncated 5-cell

Cantitruncated 5-cell
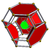Schlegel diagram with Truncated tetrahedral cells shown
Type	Uniform polychoron Uniform polychoron In geometry, a uniform polychoron is a polychoron or 4-polytope which is vertex-transitive and whose cells are uniform polyhedra....
Schläfli symbol	t0,1,2{3,3,3}
Coxeter-Dynkin diagram Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors...
Cells	20	5 (4.6.6) Truncated octahedron In geometry, the truncated octahedron is an Archimedean solid. It has 14 faces , 36 edges, and 24 vertices. Since each of its faces has point symmetry the truncated octahedron is a zonohedron.... 10 (3.4.4) Triangular prism In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides....  5 (3.6.6) Truncated tetrahedron In geometry, the truncated tetrahedron is an Archimedean solid. It has 4 regular hexagonal faces, 4 regular triangular faces, 12 vertices and 18 edges.- Area and volume :...
Faces	80	20{3} 30{4} 30{6}
Edges	120
Vertices	60
Vertex figure Vertex figure In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...	sphenoid Sphenoid Sphenoid may refer to:* In anatomy, the sphenoid bone* In geometry, a tetrahedron with mirror symmetry...
Symmetry group Coxeter group In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example...	A4, [3,3,3], order 120
Properties	convex Convex polytope A convex polytope is a special case of a polytope, having the additional property that it is also a convex set of points in the n-dimensional space Rn... , isogonal
Uniform index	6 7 8

The cantitruncated 5-cell is a uniform polychoron

Uniform polychoron

In geometry, a uniform polychoron is a polychoron or 4-polytope which is vertex-transitive and whose cells are uniform polyhedra....

. It is composed of 60 vertices, 120 edges, 80 faces, and 20 cells. The cells are: 5 truncated octahedra

Truncated octahedron

In geometry, the truncated octahedron is an Archimedean solid. It has 14 faces , 36 edges, and 24 vertices. Since each of its faces has point symmetry the truncated octahedron is a zonohedron....

, 10 triangular prism

Triangular prism

In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides....

s, and 5 truncated tetrahedra

Truncated tetrahedron

In geometry, the truncated tetrahedron is an Archimedean solid. It has 4 regular hexagonal faces, 4 regular triangular faces, 12 vertices and 18 edges.- Area and volume :...

. Each vertex is surrounded by 2 truncated octahedra, one triangular prism, and one truncated tetrahedron.

Alternative names

• Cantitruncated pentachoron
• Cantitruncated 4-simplex
  Simplex
  In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...
  
  
• Great prismatodispentachoron
• Truncated dispentachoron
• Great rhombated pentachoron (Acronym: grip) (Jonathan Bowers)

Images

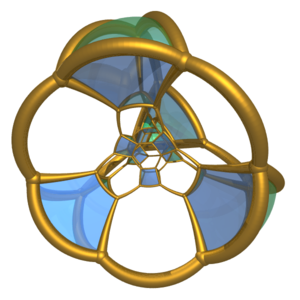Stereographic projection Stereographic projection The stereographic projection, in geometry, is a particular mapping that projects a sphere onto a plane. The projection is defined on the entire sphere, except at one point — the projection point. Where it is defined, the mapping is smooth and bijective. It is conformal, meaning that it...  with its 10 triangular prism Triangular prism In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides.... s.

Cartesian coordinates

The Cartesian coordinates of an origin-centered cantitruncated 5-cell having edge length 2 are:


These vertices can be more simply constructed on a hyperplane

Hyperplane

A hyperplane is a concept in geometry. It is a generalization of the plane into a different number of dimensions.A hyperplane of an n-dimensional space is a flat subset with dimension n − 1...

 in 5-space, as the permutation

Permutation

In mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...

s of:

(0,0,1,2,3)

This construction is from the positive orthant

Orthant

In geometry, an orthant or hyperoctant is the analogue in n-dimensional Euclidean space of a quadrant in the plane or an octant in three dimensions....

 facet of the cantitruncated 5-orthoplex.

Related polychora

These polytopes are art of a set of 9 uniform polychora

Uniform polychoron

In geometry, a uniform polychoron is a polychoron or 4-polytope which is vertex-transitive and whose cells are uniform polyhedra....

 constructed from the [3,3,3] Coxeter group

Coxeter group

In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example...

.