Truncated tesseract

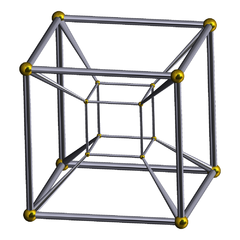Tesseract Tesseract In geometry, the tesseract, also called an 8-cell or regular octachoron or cubic prism, is the four-dimensional analog of the cube. The tesseract is to the cube as the cube is to the square. Just as the surface of the cube consists of 6 square faces, the hypersurface of the tesseract consists of 8...	Truncated tesseract	Rectified tesseract Rectified tesseract In geometry, the rectified tesseract, or rectified 8-cell is a uniform polychoron bounded by 24 cells: 8 cuboctahedra, and 16 tetrahedra....	Bitruncated tesseract
Schlegel diagrams centered on [4,3] (cells visible at [3,3])
16-cell 16-cell In four dimensional geometry, a 16-cell or hexadecachoron is a regular convex 4-polytope. It is one of the six regular convex 4-polytopes first described by the Swiss mathematician Ludwig Schläfli in the mid-19th century....	Truncated 16-cell	Rectified 16-cell (24-cell)	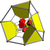Bitruncated tesseract
Schlegel diagrams centered on [3,3] (cells visible at [4,3])

In geometry

Geometry

Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....

, a truncated tesseract is a uniform polychoron

Uniform polychoron

In geometry, a uniform polychoron is a polychoron or 4-polytope which is vertex-transitive and whose cells are uniform polyhedra....

(4-dimensional uniform polytope

Polytope

In elementary geometry, a polytope is a geometric object with flat sides, which exists in any general number of dimensions. A polygon is a polytope in two dimensions, a polyhedron in three dimensions, and so on in higher dimensions...

) formed as the truncation

Truncation (geometry)

In geometry, a truncation is an operation in any dimension that cuts polytope vertices, creating a new facet in place of each vertex.- Uniform truncation :...

of the regular tesseract

Tesseract

In geometry, the tesseract, also called an 8-cell or regular octachoron or cubic prism, is the four-dimensional analog of the cube. The tesseract is to the cube as the cube is to the square. Just as the surface of the cube consists of 6 square faces, the hypersurface of the tesseract consists of 8...

.

There are three trunctions, including a bitruncation

Bitruncation

In geometry, a bitruncation is an operation on regular polytopes. It represents a truncation beyond rectification. The original edges are lost completely and the original faces remain as smaller copies of themselves....

, and a tritruncation, which creates the truncated 16-cell.

Trucated tesseract
Schlegel diagram (tetrahedron Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids... cells visible)
Type	Uniform polychoron Uniform polychoron In geometry, a uniform polychoron is a polychoron or 4-polytope which is vertex-transitive and whose cells are uniform polyhedra....
Schläfli symbol	t_0,1{4,3,3}
Coxeter-Dynkin diagram Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... s
Cells	24	8 3.8.8 Truncated cube In geometry, the truncated cube, or truncated hexahedron, is an Archimedean solid. It has 14 regular faces , 36 edges, and 24 vertices.... 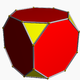16 3.3.3 Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...
Faces	88	64 {3} Triangle A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted .... 24 {8}
Edges	128
Vertices	64
Vertex figure Vertex figure In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...	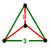Isosceles triangular pyramid
Dual	Tetrakis 16-cell
Symmetry group Coxeter group In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example...	A₄, [4,3,3]
Properties	convex Convex polytope A convex polytope is a special case of a polytope, having the additional property that it is also a convex set of points in the n-dimensional space Rn...
Uniform index	12 16-cell In four dimensional geometry, a 16-cell or hexadecachoron is a regular convex 4-polytope. It is one of the six regular convex 4-polytopes first described by the Swiss mathematician Ludwig Schläfli in the mid-19th century.... 13 14 Cantellated tesseract In four-dimensional geometry, a cantellated tesseract is a convex uniform polychoron, being a cantellation of the regular tesseract.There are four degrees of cantellations of the tesseract including with permutations truncations...

The truncated tesseract is bounded by 24 cells: 8 truncated cube

Truncated cube

In geometry, the truncated cube, or truncated hexahedron, is an Archimedean solid. It has 14 regular faces , 36 edges, and 24 vertices....

s, and 16 tetrahedra

Tetrahedron

In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...

Alternate names

Truncated tesseract (Norman W. Johnson)
Truncated tesseract (Acronym tat) (George Olshevsky
George Olshevsky
George Olshevsky is a freelance editor, writer, publisher, amateur paleontologist, and mathematician living in San Diego, California.Olshevsky maintains the comprehensive online Dinosaur Genera List...

, and Jonathan Bowers)

Construction

The truncated tesseract may be constructed by truncating

Truncation (geometry)

In geometry, a truncation is an operation in any dimension that cuts polytope vertices, creating a new facet in place of each vertex.- Uniform truncation :...

the vertices of the tesseract

Tesseract

of the edge length. A regular tetrahedron is formed at each truncated vertex.

The Cartesian coordinates of the vertices of a truncated tesseract having edge length 2 is given by all permutations of:

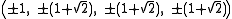
Projections

In the truncated cube first parallel projection of the truncated tesseract into 3-dimensional space, the image is laid out as follows:

The projection envelope is a cube
Cube
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and...

.
Two of the truncated cube cells project onto a truncated cube inscribed in the cubical envelope.
The other 6 truncated cubes project onto the square faces of the envelope.
The 8 tetrahedral volumes between the envelope and the triangular faces of the central truncated cube are the images of the 16 tetrahedra, a pair of cells to each image.

Images

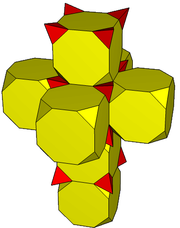A polyhedral net	Truncated tesseract projected onto the 3-sphere 3-sphere In mathematics, a 3-sphere is a higher-dimensional analogue of a sphere. It consists of the set of points equidistant from a fixed central point in 4-dimensional Euclidean space... with a stereographic projection Stereographic projection The stereographic projection, in geometry, is a particular mapping that projects a sphere onto a plane. The projection is defined on the entire sphere, except at one point — the projection point. Where it is defined, the mapping is smooth and bijective. It is conformal, meaning that it... into 3-space.

Bitruncated tesseract

Bitruncated tesseract
Two Schlegel diagrams, centered on truncated tetrahedral or truncated octahedral cells, with alternate cell types hidden.
Type	Uniform polychoron Uniform polychoron In geometry, a uniform polychoron is a polychoron or 4-polytope which is vertex-transitive and whose cells are uniform polyhedra....
Schläfli symbol	t_1,2{4,3,3} t_0,1,2{3^1,1,1}
Coxeter-Dynkin diagram Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... s
Cells	24	8 4.6.6 Truncated octahedron In geometry, the truncated octahedron is an Archimedean solid. It has 14 faces , 36 edges, and 24 vertices. Since each of its faces has point symmetry the truncated octahedron is a zonohedron.... 16 3.6.6 Truncated tetrahedron In geometry, the truncated tetrahedron is an Archimedean solid. It has 4 regular hexagonal faces, 4 regular triangular faces, 12 vertices and 18 edges.- Area and volume :...
Faces	120	32 {3} Triangle A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted .... 24 {4} Square (geometry) In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles... 64 {6}
Edges	192
Vertices	96
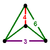Vertex figure Vertex figure In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...	Digonal disphenoid Disphenoid A disphenoid is a polyhedron whose four faces are identical triangles. The faces of a tetragonal disphenoid are isosceles; the faces of a rhombic disphenoid are scalene. If the faces are equilateral triangles, one obtains a regular tetrahedron, which is not normally considered a disphenoid.All the...
Symmetry group Coxeter group In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example...	B₄, [3,3,4] D₄, [3^1,1,1]
Properties	convex Convex polytope A convex polytope is a special case of a polytope, having the additional property that it is also a convex set of points in the n-dimensional space Rn... , vertex-transitive Vertex-transitive In geometry, a polytope is isogonal or vertex-transitive if, loosely speaking, all its vertices are the same...
Uniform index	15 Runcinated tesseract In four-dimensional geometry, a runcinated tesseract is a convex uniform polychoron, being a runcination of the regular tesseract.... 16 17

The bitruncated tesseract (also called a bitruncated 16-cell) is constructed by a bitruncation

Bitruncation

operation applied to the tesseract

Tesseract

Alternate names

Bitruncated tesseract (Norman W. Johnson)
Bitruncated tesseract (Acronym tah) (George Olshevsky
George Olshevsky
George Olshevsky is a freelance editor, writer, publisher, amateur paleontologist, and mathematician living in San Diego, California.Olshevsky maintains the comprehensive online Dinosaur Genera List...

, and Jonathan Bowers)

Construction

A tesseract is bitruncated by truncating

Truncation (geometry)

In geometry, a truncation is an operation in any dimension that cuts polytope vertices, creating a new facet in place of each vertex.- Uniform truncation :...

its cells beyond their mid-points, turning the eight cube

Cube

In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and...

s into eight truncated octahedra

Truncated octahedron

In geometry, the truncated octahedron is an Archimedean solid. It has 14 faces , 36 edges, and 24 vertices. Since each of its faces has point symmetry the truncated octahedron is a zonohedron....

. These still share their square faces, but the hexagonal faces form truncated tetrahedra which share their triangular faces with each other.

The Cartesian coordinates of the vertices of a bitruncated tesseract having edge length 2 is given by all permutations of:

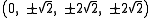
Structure

The truncated octahedra are connected to each other via their square faces, and to the truncated tetrahedra via their hexagonal faces. The truncated tetrahedra are connected to each other via their triangular faces.

Stereographic projections

The truncated-octahedron-first projection of the bitruncated tesseract into 3D space has a truncated cubical

Truncated cube

In geometry, the truncated cube, or truncated hexahedron, is an Archimedean solid. It has 14 regular faces , 36 edges, and 24 vertices....

envelope. Two of the truncated octahedral cells project onto a truncated octahedron inscribed in this envelope, with the square faces touching the centers of the octahedral faces. The 6 octahedral faces are the images of the remaining 6 truncated octahedral cells. The remaining gap between the inscribed truncated octahedron and the envelope are filled by 8 flattened truncated tetrahedra, each of which is the image of a pair of truncated tetrahedral cells.

Stereographic projection
Stereographic projection
The stereographic projection, in geometry, is a particular mapping that projects a sphere onto a plane. The projection is defined on the entire sphere, except at one point — the projection point. Where it is defined, the mapping is smooth and bijective. It is conformal, meaning that it...

s
	Colored transparently with pink triangles, blue squares, and gray hexagons

Truncated 16-cell

Truncated 16-cell
Schlegel diagram (octahedron Octahedron In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex.... cells visible)
Type	Uniform polychoron Uniform polychoron In geometry, a uniform polychoron is a polychoron or 4-polytope which is vertex-transitive and whose cells are uniform polyhedra....
Schläfli symbol	t_0,1{4,3,3} t_0,1{3^1,1,1}
Coxeter-Dynkin diagram Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... s
Cells	24	8 3.3.3.3 Octahedron In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex.... 16 3.6.6 Truncated tetrahedron In geometry, the truncated tetrahedron is an Archimedean solid. It has 4 regular hexagonal faces, 4 regular triangular faces, 12 vertices and 18 edges.- Area and volume :...
Faces	96	64 {3} Triangle A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted .... 32 {6}
Edges	120
Vertices	48
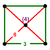Vertex figure Vertex figure In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...	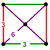square pyramid Square pyramid In geometry, a square pyramid is a pyramid having a square base. If the apex is perpendicularly above the center of the square, it will have C4v symmetry.- Johnson solid :...
Dual	Hexakis tesseract
Coxeter groups	BC₄ [3,3,4] D₄ [3^1,1,1]
Properties	convex Convex polytope A convex polytope is a special case of a polytope, having the additional property that it is also a convex set of points in the n-dimensional space Rn...
Uniform index	16 17 18

The truncated 16-cell which is bounded by 24 cells: 8 regular octahedra

Octahedron

In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....

, and 16 truncated tetrahedra

Truncated tetrahedron

In geometry, the truncated tetrahedron is an Archimedean solid. It has 4 regular hexagonal faces, 4 regular triangular faces, 12 vertices and 18 edges.- Area and volume :...

.

It is related to, but not to be confused with, the 24-cell, which is a regular polychoron bounded by 24 regular octahedra.

Alternate names

Truncated 16-cell (Norman W. Johnson)
Truncated hexadecachoron (Acronym thex) (George Olshevsky
George Olshevsky
George Olshevsky is a freelance editor, writer, publisher, amateur paleontologist, and mathematician living in San Diego, California.Olshevsky maintains the comprehensive online Dinosaur Genera List...

, and Jonathan Bowers)

Construction

The truncated 16-cell may be constructed from the 16-cell

16-cell

In four dimensional geometry, a 16-cell or hexadecachoron is a regular convex 4-polytope. It is one of the six regular convex 4-polytopes first described by the Swiss mathematician Ludwig Schläfli in the mid-19th century....

by truncating its vertices at 1/3 of the edge length. This results in the 16 truncated tetrahedral cells, and introduces the 8 octahedra (vertex figures).

(Truncating a 16-cell at 1/2 of the edge length results in the 24-cell, which has a greater degree of symmetry because the truncated cells become identical with the vertex figures.)

The Cartesian coordinates of the vertices of a truncated 16-cell having edge length 2√2 are given by all permutations, and sign combinations:

(0,0,1,2)

An alternate construction begins with a demitesseract with vertex coordinates (±3,±3,±3,±3), having an even number of each sign, and truncates it to obtain the permutations of

(1,1,3,3), with an even number of each sign.

Structure

The truncated tetrahedra are joined to each other via their hexagonal faces. The octahedra are joined to the truncated tetrahedra via their triangular faces.

Centered on octahedron

The octahedron-first parallel projection of the truncated 16-cell into 3-dimensional space has the following structure:

The projection envelope is a truncated octahedron
Truncated octahedron
In geometry, the truncated octahedron is an Archimedean solid. It has 14 faces , 36 edges, and 24 vertices. Since each of its faces has point symmetry the truncated octahedron is a zonohedron....

.
The 6 square faces of the envelope are the images of 6 of the octahedral cells.
An octahedron lies at the center of the envelope, joined to the center of the 6 square faces by 6 edges. This is the image of the other 2 octahedral cells.
The remaining space between the envelope and the central octahedron is filled by 8 truncated tetrahedra (distorted by projection). These are the images of the 16 truncated tetrahedral cells, a pair of cells to each image.

This layout of cells in projection is analogous to the layout of faces in the projection of the truncated octahedron

Truncated octahedron

In geometry, the truncated octahedron is an Archimedean solid. It has 14 faces , 36 edges, and 24 vertices. Since each of its faces has point symmetry the truncated octahedron is a zonohedron....

into 2-dimensional space. Hence, the truncated 16-cell may be thought of as the 4-dimensional analogue of the truncated octahedron.

Centered on truncated tetrahedron

The truncated tetrahedron first parallel projection of the truncated 16-cell into 3-dimensional space has the following structure:

The projection envelope is a truncated cube
Truncated cube
In geometry, the truncated cube, or truncated hexahedron, is an Archimedean solid. It has 14 regular faces , 36 edges, and 24 vertices....

.
The nearest truncated tetrahedron to the 4D viewpoint projects to the center of the envelope, with its triangular faces joined to 4 octahedral volumes that connect it to 4 of the triangular faces of the envelope.
The remaining space in the envelope is filled by 4 other truncated tetrahedra.
These volumes are the images of the cells lying on the near side of the truncated 16-cell; the other cells project onto the same layout except in the dual configuration.
The six octagonal faces of the projection envelope are the images of the remaining 6 truncated tetrahedral cells.

Images

net	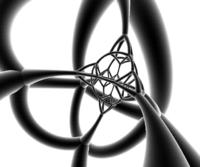stereographic projection Stereographic projection The stereographic projection, in geometry, is a particular mapping that projects a sphere onto a plane. The projection is defined on the entire sphere, except at one point — the projection point. Where it is defined, the mapping is smooth and bijective. It is conformal, meaning that it... (centered on truncated tetrahedron Truncated tetrahedron In geometry, the truncated tetrahedron is an Archimedean solid. It has 4 regular hexagonal faces, 4 regular triangular faces, 12 vertices and 18 edges.- Area and volume :... )

External links

Paper model of truncated tesseract created using nets generated by Stella4D
Stella (software)
Stella, a computer program available in three versions was created by Robert Webb of Australia...

software

The source of this article is wikipedia, the free encyclopedia. The text of this article is licensed under the GFDL.