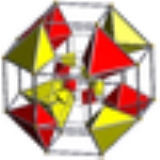
Cantellated tesseract

Four cantellations
Orthogonal projections in A₄ Coxeter plane
tesseract Tesseract In geometry, the tesseract, also called an 8-cell or regular octachoron or cubic prism, is the four-dimensional analog of the cube. The tesseract is to the cube as the cube is to the square. Just as the surface of the cube consists of 6 square faces, the hypersurface of the tesseract consists of 8...	Cantellated tesseract	Cantellated 16-cell (Rectified 24-cell Rectified 24-cell In geometry, the rectified 24-cell is a uniform 4-dimensional polytope , which is bounded by 48 cells: 24 cubes, and 24 cuboctahedra. It can be obtained by reducing the icositetrachoron's cells to cubes or cuboctahedra.... )
16-cell 16-cell In four dimensional geometry, a 16-cell or hexadecachoron is a regular convex 4-polytope. It is one of the six regular convex 4-polytopes first described by the Swiss mathematician Ludwig Schläfli in the mid-19th century....	Cantitruncated tesseract	Cantitruncated 16-cell (Truncated 24-cell Truncated 24-cell In geometry, a truncated 5-cell is a uniform polychoron formed as the truncation of the regular 5-cell.There are two degrees of trunctions, including a bitruncation.- Truncated 5-cell:... )

In four-dimensional geometry

Geometry

Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....

, a cantellated tesseract is a convex uniform polychoron

Uniform polychoron

In geometry, a uniform polychoron is a polychoron or 4-polytope which is vertex-transitive and whose cells are uniform polyhedra....

, being a cantellation (a 2nd order truncation) of the regular tesseract

Tesseract

In geometry, the tesseract, also called an 8-cell or regular octachoron or cubic prism, is the four-dimensional analog of the cube. The tesseract is to the cube as the cube is to the square. Just as the surface of the cube consists of 6 square faces, the hypersurface of the tesseract consists of 8...

.

There are four degrees of cantellations of the tesseract including with permutations truncations. Two are also derived from the 24-cell family.

Cantellated tesseract
Schlegel diagram Centered on rhombicuboctahedron octahedral cells shown
Type	Uniform polychoron Uniform polychoron In geometry, a uniform polychoron is a polychoron or 4-polytope which is vertex-transitive and whose cells are uniform polyhedra....
Schläfli symbol	t_0,2{4,3,3}
Coxeter-Dynkin diagram Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors...
Cells	56	8 3.4.4.4 16 3.3.3.3 Octahedron In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex.... 32 3.4.4 Triangular prism In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides....
Faces	248	128 {3} Triangle A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted .... 120 {4} Square (geometry) In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles...
Edges	288
Vertices	96
Vertex figure Vertex figure In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...	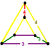Square wedge
Symmetry group Coxeter group In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example...	B₄, [3,3,4]
Properties	convex Convex polytope A convex polytope is a special case of a polytope, having the additional property that it is also a convex set of points in the n-dimensional space Rn...
Uniform index	13 Truncated tesseract In geometry, a truncated tesseract is a uniform polychoron formed as the truncation of the regular tesseract.There are three trunctions, including a bitruncation, and a tritruncation, which creates the truncated 16-cell.... 14 15 Runcinated tesseract In four-dimensional geometry, a runcinated tesseract is a convex uniform polychoron, being a runcination of the regular tesseract....

The cantellated tesseract (or bicantellated 16-cell) is a convex uniform polychoron

Uniform polychoron

In geometry, a uniform polychoron is a polychoron or 4-polytope which is vertex-transitive and whose cells are uniform polyhedra....

or 4-dimensional polytope

Polytope

In elementary geometry, a polytope is a geometric object with flat sides, which exists in any general number of dimensions. A polygon is a polytope in two dimensions, a polyhedron in three dimensions, and so on in higher dimensions...

bounded by 56 cells: 8 small rhombicuboctahedra, 16 octahedra

Octahedron

In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....

, and 32 triangular prism

Triangular prism

In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides....

Construction

In the process of cantellation

Cantellation (geometry)

In geometry, a cantellation is an operation in any dimension that cuts a regular polytope at its edges and vertices, creating a new facet in place of each edge and vertex. The operation also applies to regular tilings and honeycombs...

, a polytope's 2-faces are effectively shrunk. The rhombicuboctahedron

Rhombicuboctahedron

In geometry, the rhombicuboctahedron, or small rhombicuboctahedron, is an Archimedean solid with eight triangular and eighteen square faces. There are 24 identical vertices, with one triangle and three squares meeting at each. Note that six of the squares only share vertices with the triangles...

can be called a cantellated cube, since if its six faces are shrunk in their respective planes, each vertex will separate into the three vertices of the rhombicuboctahedron's triangles, and each edge will separate into two of the opposite edges of the rhombicuboctahedrons twelve non-axial squares.

When the same process is applied to the tesseract, each of the eight cubes becomes a rhombicuboctahedron in the described way. In addition however, since each cube's edge was previously shared with two other cubes, the separating edges form the three parallel edges of a triangular prism—32 triangular prisms, since there were 32 edges. Further, since each vertex was previously shared with three other cubes, the vertex would split into 12 rather than three new vertices. However, since some of the shrunken faces continues to be shared, certain pairs of these 12 potential vertices are identical to each other, and therefore only 6 new vertices are created from each original vertex (hence the cantellated tesseract's 96 vertices compared to the tesseract's 16). These six new vertices form the vertices of an octahedron—16 octahedra, since the tesseract had 16 vertices.

Cartesian coordinates

The Cartesian coordinates of the vertices of a cantellated tesseract with edge length 2 is given by all permutations of: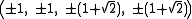

Structure

The 8 small rhombicuboctahedral cells are joined to each other via their axial square faces. Their non-axial square faces, which correspond with the edges of a cube, are connected to the triangular prisms. The triangular faces of the small rhombicuboctahedra and the triangular prisms are connected to the 16 octahedra.

Its structure can be imagined by means of the tesseract itself: the rhombicuboctahedra are analogous to the tesseract's cells, the triangular prisms are analogous to the tesseract's edges, and the octahedra are analogous to the tesseract's vertices.

Images

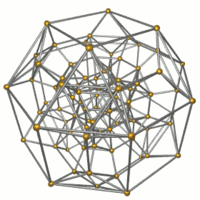Wireframe	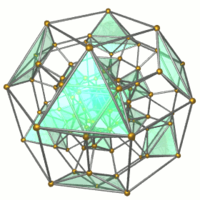16 octahedra Octahedron In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex.... shown.	32 triangular prism Triangular prism In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides.... s shown.

Projections

The following is the layout of the cantellated tesseract's cells under the parallel projection into 3-dimensional space, small rhombicuboctahedron first:

The projection envelope is a truncated cube
Truncated cube
In geometry, the truncated cube, or truncated hexahedron, is an Archimedean solid. It has 14 regular faces , 36 edges, and 24 vertices....

.
The nearest and farthest small rhombicuboctahedral cells from the 4D viewpoint project to the volume of the same shape inscribed in the projection envelope.
The axial squares of this central small rhombicuboctahedron touches the centers of the 6 octagons of the envelope. The octagons are the image of the other 6 small rhombicuboctahedral cells.
The 12 wedge-shaped volumes connecting the non-axial square faces of the central small rhombicuboctahedron to the neighbouring octagons are the images of 24 of the triangular prisms.
The remaining 8 triangular prisms project onto the triangular faces of the envelope.
Between the triangular faces of the envelope and the triangular faces of the central small rhombicuboctahedron are 8 octahedral volumes, which are the images of the 16 octahedral cells.

This layout of cells in projection is analogous to the layout of faces in the projection of the truncated cube

Truncated cube

In geometry, the truncated cube, or truncated hexahedron, is an Archimedean solid. It has 14 regular faces , 36 edges, and 24 vertices....

into 2 dimensions. Hence, the cantellated tesseract may be thought of as an analogue of the truncated cube in 4 dimensions. (It is not the only possible analogue; another close candidate is the truncated tesseract

Truncated tesseract

In geometry, a truncated tesseract is a uniform polychoron formed as the truncation of the regular tesseract.There are three trunctions, including a bitruncation, and a tritruncation, which creates the truncated 16-cell....

.)

Another uniform polychoron with a similar layout of cells is the runcitruncated 16-cell.

Cantitruncated tesseract

Cantitruncated tesseract
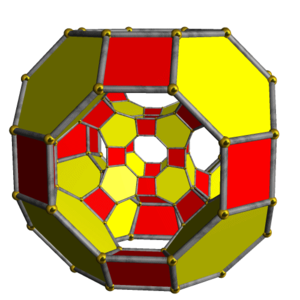Schlegel diagram centered on great rhombicuboctahedron cell with octagonal faces hidden.
Type	Uniform polychoron Uniform polychoron In geometry, a uniform polychoron is a polychoron or 4-polytope which is vertex-transitive and whose cells are uniform polyhedra....
Schläfli symbol	t_0,1,2{4,3,3}
Coxeter-Dynkin diagram Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... s
Cells	56	8 4.6.8 16 3.6.6 Truncated tetrahedron In geometry, the truncated tetrahedron is an Archimedean solid. It has 4 regular hexagonal faces, 4 regular triangular faces, 12 vertices and 18 edges.- Area and volume :... 32 3.4.4 Triangular prism In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides....
Faces	248	64 {3} Triangle A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted .... , 96 {4} Square (geometry) In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles... 64 {6}, 24 {8}
Edges	384
Vertices	192
Vertex figure Vertex figure In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...	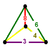Sphenoid Sphenoid Sphenoid may refer to:* In anatomy, the sphenoid bone* In geometry, a tetrahedron with mirror symmetry...
Symmetry group Coxeter group In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example...	B₄, [3,3,4]
Properties	convex Convex polytope A convex polytope is a special case of a polytope, having the additional property that it is also a convex set of points in the n-dimensional space Rn...
Uniform index	17 18 19

In geometry

Geometry

Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....

, the cantitruncated tesseract is a uniform polychoron

Uniform polychoron

In geometry, a uniform polychoron is a polychoron or 4-polytope which is vertex-transitive and whose cells are uniform polyhedra....

(or uniform 4-dimensional polytope

Polytope

) that is bounded by 56 cells: 8 truncated cuboctahedra

Truncated cuboctahedron

In geometry, the truncated cuboctahedron is an Archimedean solid. It has 12 square faces, 8 regular hexagonal faces, 6 regular octagonal faces, 48 vertices and 72 edges...

, 16 truncated tetrahedra

Truncated tetrahedron

In geometry, the truncated tetrahedron is an Archimedean solid. It has 4 regular hexagonal faces, 4 regular triangular faces, 12 vertices and 18 edges.- Area and volume :...

, and 32 triangular prism

Triangular prism

In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides....

Construction

The cantitruncated tesseract is constructed by the cantitruncation of the tesseract

Tesseract

.
Cantitruncation is often thought of as rectification followed by truncation. However, the result of this construction would be a polytope which, while its structure would be very similar to that given by cantitruncation, not all of its faces would be uniform.

Alternatively, a uniform cantitruncated tesseract may be constructed by placing 8 uniform truncated cuboctahedra

Truncated cuboctahedron

In geometry, the truncated cuboctahedron is an Archimedean solid. It has 12 square faces, 8 regular hexagonal faces, 6 regular octagonal faces, 48 vertices and 72 edges...

in the hyperplanes of a tesseract's cells, displaced along the coordinate axes such that their octagonal faces coincide. For an edge length of 2, this construction gives the Cartesian coordinates of its vertices as all permutations of:

Structure

The 8 truncated cuboctahedra are joined to each other via their octagonal faces, in an arrangement corresponding to the 8 cubical cells of the tesseract. They are joined to the 16 truncated tetrahedra via their hexagonal faces, and their square faces are joined to the square faces of the 32 triangular prisms. The triangular faces of the triangular prisms are joined to the truncated tetrahedra.

The truncated tetrahedra correspond with the tesseract's vertices, and the triangular prisms correspond with the tesseract's edges.

Images

A stereographic projection Stereographic projection The stereographic projection, in geometry, is a particular mapping that projects a sphere onto a plane. The projection is defined on the entire sphere, except at one point — the projection point. Where it is defined, the mapping is smooth and bijective. It is conformal, meaning that it... of the cantellated tesseract, as a tiling on a 3-sphere 3-sphere In mathematics, a 3-sphere is a higher-dimensional analogue of a sphere. It consists of the set of points equidistant from a fixed central point in 4-dimensional Euclidean space... , with its 64 blue triangular faces, 96 green quad faces and 64 red hexagonal faces (the octagonal faces are not drawn).

Projections

In the truncated cuboctahedron first parallel projection into 3 dimensions, the cells of the cantitruncated tesseract are laid out as follows:

The projection envelope is a non-uniform truncated cube
Truncated cube
In geometry, the truncated cube, or truncated hexahedron, is an Archimedean solid. It has 14 regular faces , 36 edges, and 24 vertices....

, with longer edges between octagons and shorter edges in the 8 triangles.
The irregular octagonal faces of the envelope correspond with the images of 6 of the 8 truncated cuboctahedral cells.
The other two truncated cuboctahedral cells project to a truncated cuboctahedron inscribed in the projection envelope. The octagonal faces touch the irregular octagons of the envelope.
In the spaces corresponding to a cube's edges lie 12 volumes in the shape of irregular triangular prisms. These are the images, one per pair, of 24 of the triangular prism cells.
The remaining 8 triangular prisms project onto the triangular faces of the projection envelope.
The remaining 8 spaces, corresponding to a cube's corners, are the images of the 16 truncated tetrahedra, a pair to each space.

This layout of cells in projection is similar to that of the cantellated tesseract

Cantellated tesseract

In four-dimensional geometry, a cantellated tesseract is a convex uniform polychoron, being a cantellation of the regular tesseract.There are four degrees of cantellations of the tesseract including with permutations truncations...

Alternative names

Cantitruncated tesseract (Norman W. Johnson)
Cantitruncated 4-cube
Cantitruncated 8-cell
Cantitruncated octachoron
Great prismatotesseractihexadecachoron (George Olshevsky
George Olshevsky
George Olshevsky is a freelance editor, writer, publisher, amateur paleontologist, and mathematician living in San Diego, California.Olshevsky maintains the comprehensive online Dinosaur Genera List...

)
Grit (Jonathan Bowers: for great rhombated tesseract)
012-ambo tesseract (John Conway
John Horton Conway
John Horton Conway is a prolific mathematician active in the theory of finite groups, knot theory, number theory, combinatorial game theory and coding theory...

)

The source of this article is wikipedia, the free encyclopedia. The text of this article is licensed under the GFDL.