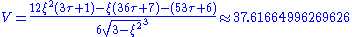Snub dodecahedron
Encyclopedia
In geometry
, the snub dodecahedron, or snub icosidodecahedron, is an Archimedean solid
, one of thirteen convex isogonal nonprismatic solids constructed by two or more types of regular polygon
face
s.
The snub dodecahedron has 92 faces (the most of any convex uniform polyhedron other than prism
s and antiprism
s), of which 12 are pentagon
s and the other 80 are equilateral triangles. It also has 150 edges, and 60 vertices. It has two distinct forms, which are mirror image
s (or "enantiomorphs
") of each other.
al faces of the dodecahedron and pulling them outward
so they no longer touch. At a proper distance this can create the rhombicosidodecahedron
by filling in square faces between the divided edges and triangle faces between the divided vertices. But for the snub form, only add the triangle faces and leave the square gaps empty. Then apply an equal rotation to the centers of the pentagons and triangles, continuing the rotation until the gaps can be filled by two equilateral triangles.
The snub dodecahedron can also be derived from the truncated icosidodecahedron
by the process of alternation. Sixty of the vertices of the truncated icosidodecahedron form a polyhedron topologically equivalent to one snub dodecahedron; the remaining 60 form its mirror-image. The resulting polyhedron is vertex-transitive
but not uniform, because its edges are of unequal lengths; some deformation is required to transform it into a uniform polyhedron.
Archimedes
, an ancient Greek who showed major interest in polyhedral shapes, wrote a treatise on thirteen semi-regular solids. The snub dodecahedron is one of them.
with an even number of plus signs, where
and
where τ = (1+√5)/2 is the golden ratio
and
ξ is the real solution to ξ3-2ξ=τ, which is the number:

or approximately 1.7155615.
This snub dodecahedron has an edge length of approximately 6.0437380841.
Taking the even permutations of the above coordinates with an odd number of plus signs gives another form, the enantiomorph
of the other one.
and the volume is
where τ is the golden ratio
.
Snub dodecahedron has the highest sphericity of all Archimedean solids.
polyhedra and tilings with vertex figure (3.3.3.3.p) and Coxeter-Dynkin diagram
. These face-transitive figures have (n32) rotational symmetry.
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, the snub dodecahedron, or snub icosidodecahedron, is an Archimedean solid
Archimedean solid
In geometry an Archimedean solid is a highly symmetric, semi-regular convex polyhedron composed of two or more types of regular polygons meeting in identical vertices...
, one of thirteen convex isogonal nonprismatic solids constructed by two or more types of regular polygon
Regular polygon
A regular polygon is a polygon that is equiangular and equilateral . Regular polygons may be convex or star.-General properties:...
face
Face (geometry)
In geometry, a face of a polyhedron is any of the polygons that make up its boundaries. For example, any of the squares that bound a cube is a face of the cube...
s.
The snub dodecahedron has 92 faces (the most of any convex uniform polyhedron other than prism
Prism (geometry)
In geometry, a prism is a polyhedron with an n-sided polygonal base, a translated copy , and n other faces joining corresponding sides of the two bases. All cross-sections parallel to the base faces are the same. Prisms are named for their base, so a prism with a pentagonal base is called a...
s and antiprism
Antiprism
In geometry, an n-sided antiprism is a polyhedron composed of two parallel copies of some particular n-sided polygon, connected by an alternating band of triangles...
s), of which 12 are pentagon
Pentagon
In geometry, a pentagon is any five-sided polygon. A pentagon may be simple or self-intersecting. The sum of the internal angles in a simple pentagon is 540°. A pentagram is an example of a self-intersecting pentagon.- Regular pentagons :In a regular pentagon, all sides are equal in length and...
s and the other 80 are equilateral triangles. It also has 150 edges, and 60 vertices. It has two distinct forms, which are mirror image
Mirror image
A mirror image is a reflected duplication of an object that appears identical but reversed. As an optical effect it results from reflection off of substances such as a mirror or water. It is also a concept in geometry and can be used as a conceptualization process for 3-D structures...
s (or "enantiomorphs
Chirality (mathematics)
In geometry, a figure is chiral if it is not identical to its mirror image, or, more precisely, if it cannot be mapped to its mirror image by rotations and translations alone. For example, a right shoe is different from a left shoe, and clockwise is different from counterclockwise.A chiral object...
") of each other.
Geometric relations
The snub dodecahedron can be generated by taking the twelve pentagonPentagon
In geometry, a pentagon is any five-sided polygon. A pentagon may be simple or self-intersecting. The sum of the internal angles in a simple pentagon is 540°. A pentagram is an example of a self-intersecting pentagon.- Regular pentagons :In a regular pentagon, all sides are equal in length and...
al faces of the dodecahedron and pulling them outward
Expansion (geometry)
In geometry, expansion is a polytope operation where facets are separated and moved radially apart, and new facets are formed at separated elements...
so they no longer touch. At a proper distance this can create the rhombicosidodecahedron
Rhombicosidodecahedron
In geometry, the rhombicosidodecahedron, or small rhombicosidodecahedron, is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids constructed of two or more types of regular polygon faces....
by filling in square faces between the divided edges and triangle faces between the divided vertices. But for the snub form, only add the triangle faces and leave the square gaps empty. Then apply an equal rotation to the centers of the pentagons and triangles, continuing the rotation until the gaps can be filled by two equilateral triangles.
 Dodecahedron |
 Rhombicosidodecahedron (Expanded dodecahedron) |
The snub dodecahedron can also be derived from the truncated icosidodecahedron
Truncated icosidodecahedron
In geometry, the truncated icosidodecahedron is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids constructed by two or more types of regular polygon faces....
by the process of alternation. Sixty of the vertices of the truncated icosidodecahedron form a polyhedron topologically equivalent to one snub dodecahedron; the remaining 60 form its mirror-image. The resulting polyhedron is vertex-transitive
Vertex-transitive
In geometry, a polytope is isogonal or vertex-transitive if, loosely speaking, all its vertices are the same...
but not uniform, because its edges are of unequal lengths; some deformation is required to transform it into a uniform polyhedron.
Archimedes
Archimedes
Archimedes of Syracuse was a Greek mathematician, physicist, engineer, inventor, and astronomer. Although few details of his life are known, he is regarded as one of the leading scientists in classical antiquity. Among his advances in physics are the foundations of hydrostatics, statics and an...
, an ancient Greek who showed major interest in polyhedral shapes, wrote a treatise on thirteen semi-regular solids. The snub dodecahedron is one of them.
Cartesian coordinates
Cartesian coordinates for the vertices of a snub dodecahedron are all the even permutations of- (±2α, ±2, ±2β),
- (±(α+β/τ+τ), ±(-ατ+β+1/τ), ±(α/τ+βτ-1)),
- (±(-α/τ+βτ+1), ±(-α+β/τ-τ), ±(ατ+β-1/τ)),
- (±(-α/τ+βτ-1), ±(α-β/τ-τ), ±(ατ+β+1/τ)) and
- (±(α+β/τ-τ), ±(ατ-β+1/τ), ±(α/τ+βτ+1)),
with an even number of plus signs, where
- α = ξ-1/ξ
and
- β = ξτ+τ2+τ/ξ,
where τ = (1+√5)/2 is the golden ratio
Golden ratio
In mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989...
and
ξ is the real solution to ξ3-2ξ=τ, which is the number:

or approximately 1.7155615.
This snub dodecahedron has an edge length of approximately 6.0437380841.
Taking the even permutations of the above coordinates with an odd number of plus signs gives another form, the enantiomorph
Chirality (mathematics)
In geometry, a figure is chiral if it is not identical to its mirror image, or, more precisely, if it cannot be mapped to its mirror image by rotations and translations alone. For example, a right shoe is different from a left shoe, and clockwise is different from counterclockwise.A chiral object...
of the other one.
Surface area and volume
For a snub dodecahedron whose edge length is 1, the surface area isand the volume is
where τ is the golden ratio
Golden ratio
In mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989...
.
Snub dodecahedron has the highest sphericity of all Archimedean solids.
Related polyhedra and tilings
This semiregular polyhedron is a member of a sequence of snubbedSnub (geometry)
In geometry, an alternation is an operation on a polyhedron or tiling that removes alternate vertices. Only even-sided polyhedra can be alternated, for example the zonohedra. Every 2n-sided face becomes n-sided...
polyhedra and tilings with vertex figure (3.3.3.3.p) and Coxeter-Dynkin diagram
Coxeter-Dynkin diagram
In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors...
. These face-transitive figures have (n32) rotational symmetry.
 (3.3.3.3.3) Icosahedron In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids.... (332) |
 (3.3.3.3.4) Snub cube In geometry, the snub cube, or snub cuboctahedron, is an Archimedean solid.The snub cube has 38 faces, 6 of which are squares and the other 32 are equilateral triangles. It has 60 edges and 24 vertices. It is a chiral polyhedron, that is, it has two distinct forms, which are mirror images of each... (432) |
 (3.3.3.3.5) Snub dodecahedron In geometry, the snub dodecahedron, or snub icosidodecahedron, is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids constructed by two or more types of regular polygon faces.... (532) |
 3.3.3.3.6 Snub hexagonal tiling In geometry, the Snub hexagonal tiling is a semiregular tiling of the Euclidean plane. There are four triangles and one hexagon on each vertex... (632) |
 3.3.3.3.7 (732) |
 3.3.3.3.8 (832) |
See also
- ccw and cw spinning snub dodecahedron
External links
- http://www.dr-mikes-math-games-for-kids.com/polyhedral-nets.html?net=aDiAd7EuD6JEyMy1JVKFsa8iDW5tM3Qs3MqxBVGvmd0694UNAzjcvcRXcqBcC0KGnIBi7h9Cg3w8ikfFW8uoxM4d8N02mUmiPtVdjRPES3K1YArAm20bjfn9nWCHZyBubfS1uMff57mXxR7FJJfAfnu4OcLgXVVXORgYnVJIjjFwCcT2i1hLxuYbchkA5VGUKE1Xrvjw5arGCHafH9uIWvTT0ZGeb7LJ5C90hu7ALyKfc9C7vxnyqc2dVwmoXQSD9kc84xzoZiGGWx4MyhCpjnD5MVLpy8LssafhN1eSm2ZrUT4snKGowFy8b3ZbTsWtLD0HPNYfZWrbvpgWhE4ToCjGOOKXWnUT3qflcKZLGxwRrv5gWaxKZeBPQNwvRohjtyI96MJL5N1lz9FLKmEQbwliTaWaqBK7aWIiuMjhMxo3QghFTa1mLqvtZFll4OOyKnnjWe3uWAW0AX6tYWUEhElXF1f5QM9zSeKxr80WxlOQUXS875Be7s7cirEkBwiwTzNbQkQCjC3UlMHw05WygS2LQzqhxoLVDIW43poA7RxsZzZ54x9kBmVeMuZDYJPVFPGFJiOOHk2SwSMB1E4UmlEZb2LKxNr19bc3YnVn06RJjG2F5y5pbzKdyq1J0tZ5aX7Mi61LcreSoHOrO5teQDDQL7bkqcPixbpxQCSmX7jVCGFzLqgZF3c9t56VBAmM8FcR&name=Snub+Dodecahedron#appletEditable printable net of a Snub Dodecahedron with interactive 3D view]
- The Uniform Polyhedra
- Virtual Reality Polyhedra The Encyclopedia of Polyhedra
- The Snub Dodecahedron made with LEGO by Antonio Nicassio (ITALY)