Sphericity is a measure of how spherical (round) an object is. As such, it is a specific example of a compactness measure of a shape

Compactness measure of a shape

The compactness measure of a shape, sometimes called the shape factor, is a numerical quantity representing the degree to which a shape is compact. The meaning of "compact" here is not related to the topological notion of compact space. Various compactness measures are used...

. Defined by Wadell in 1935, the sphericity, 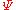, of a particle is the ratio of the surface area

Surface area

Surface area is the measure of how much exposed area a solid object has, expressed in square units. Mathematical description of the surface area is considerably more involved than the definition of arc length of a curve. For polyhedra the surface area is the sum of the areas of its faces...

 of a sphere

Sphere

A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...

 (with the same volume

Volume

Volume is the quantity of three-dimensional space enclosed by some closed boundary, for example, the space that a substance or shape occupies or contains....

 as the given particle) to the surface area of the particle:


where is volume of the particle and 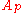is the surface area of the particle
The sphericity, 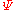, of an oblate spheroid (similar to the shape of the planet Earth

Earth

Earth is the third planet from the Sun, and the densest and fifth-largest of the eight planets in the Solar System. It is also the largest of the Solar System's four terrestrial planets...

) is defined as such:


(where a, b are the semi-major

Semi-major axis

The major axis of an ellipse is its longest diameter, a line that runs through the centre and both foci, its ends being at the widest points of the shape...

, semi-minor

Semi-minor axis

In geometry, the semi-minor axis is a line segment associated with most conic sections . One end of the segment is the center of the conic section, and it is at right angles with the semi-major axis...

 axes, respectively.
Hakon Wadell defined sphericity as the surface area of a
sphere of the same volume as the particle divided by the actual surface area of the particle.

First we need to write surface area of the sphere, 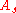in terms of the volume of the particle,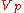


therefore


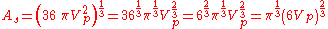
hence we define as: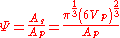


In statistical analyses, sphericity relates to the equality of the variance

Variance

In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...

s of the differences between levels of the repeated measures factor.