
Compactness measure of a shape
Encyclopedia
The compactness measure of a shape
, sometimes called the shape factor
, is a numerical quantity representing the degree to which a shape is compact. The meaning of "compact" here is not related to the topological notion of compact space
. Various compactness measures are used. However, these measures have the following in common:
A common compactness measure is the Isoperimetric quotient, the ratio of the area of the shape to the area of a circle
(the most compact shape) having the same perimeter.
Compactness measures can be defined for three-dimensional shapes as well, typically as functions of volume
and surface area
. One example of a compactness measure is sphericity Ψ. Another measure in use is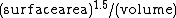 .
.
A common use of compactness measures is in redistricting
. The goal is to maximize the compactness of electoral districts, subject to other constraints, and thereby to avoid gerrymandering
. Another use is in zoning
, to regulate the manner in which land can be subdivided into building lots
.
Another use is in pattern classification projects so that you can classify the circle from other shapes.
Shape
The shape of an object located in some space is a geometrical description of the part of that space occupied by the object, as determined by its external boundary – abstracting from location and orientation in space, size, and other properties such as colour, content, and material...
, sometimes called the shape factor
Shape factor
Shape factor can refer to one of number of values in physics, engineering, or image analysis. Typically, a shape factor refers to a value that is affected by an object's shape but is independent of its dimensions.In physics:...
, is a numerical quantity representing the degree to which a shape is compact. The meaning of "compact" here is not related to the topological notion of compact space
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
. Various compactness measures are used. However, these measures have the following in common:
- They are applicable to all geometric shapes.
- They are independent of scale and orientation.
- They are dimensionless numbers.
- They are not overly dependent on one or two extreme pointsPoint (geometry)In geometry, topology and related branches of mathematics a spatial point is a primitive notion upon which other concepts may be defined. In geometry, points are zero-dimensional; i.e., they do not have volume, area, length, or any other higher-dimensional analogue. In branches of mathematics...
in the shape. - They agree with intuitive notions of what makes a shape compact.
A common compactness measure is the Isoperimetric quotient, the ratio of the area of the shape to the area of a circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
(the most compact shape) having the same perimeter.
Compactness measures can be defined for three-dimensional shapes as well, typically as functions of volume
Volume
Volume is the quantity of three-dimensional space enclosed by some closed boundary, for example, the space that a substance or shape occupies or contains....
and surface area
Area
Area is a quantity that expresses the extent of a two-dimensional surface or shape in the plane. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat...
. One example of a compactness measure is sphericity Ψ. Another measure in use is
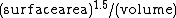 .
.A common use of compactness measures is in redistricting
Redistricting
Redistricting is the process of drawing United States electoral district boundaries, often in response to population changes determined by the results of the decennial census. In 36 states, the state legislature has primary responsibility for creating a redistricting plan, in many cases subject to...
. The goal is to maximize the compactness of electoral districts, subject to other constraints, and thereby to avoid gerrymandering
Gerrymandering
In the process of setting electoral districts, gerrymandering is a practice that attempts to establish a political advantage for a particular party or group by manipulating geographic boundaries to create partisan, incumbent-protected districts...
. Another use is in zoning
Zoning
Zoning is a device of land use planning used by local governments in most developed countries. The word is derived from the practice of designating permitted uses of land based on mapped zones which separate one set of land uses from another...
, to regulate the manner in which land can be subdivided into building lots
Lot (real estate)
In real estate, a lot or plot is a tract or parcel of land owned or meant to be owned by some owner. A lot is essentially considered a parcel of real property in some countries or immovable property in other countries...
.
Another use is in pattern classification projects so that you can classify the circle from other shapes.
See also
- Surface area to volume ratioSurface area to volume ratioThe surface-area-to-volume ratio also called the surface-to-volume ratio and variously denoted sa/vol or SA:V, is the amount of surface area per unit volume of an object or collection of objects. The surface-area-to-volume ratio is measured in units of inverse distance. A cube with sides of...
- How Long Is the Coast of Britain? Statistical Self-Similarity and Fractional DimensionHow Long Is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension"How Long Is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension" is a paper by mathematician Benoît Mandelbrot, first published in Science in 1967. In this paper Mandelbrot discusses self-similar curves that have Hausdorff dimension between 1 and 2...

