In geometry

Geometry

Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....

, the semi-minor axis (also semiminor axis) is a line segment

Line segment

In geometry, a line segment is a part of a line that is bounded by two end points, and contains every point on the line between its end points. Examples of line segments include the sides of a triangle or square. More generally, when the end points are both vertices of a polygon, the line segment...

 associated with most conic section

Conic section

In mathematics, a conic section is a curve obtained by intersecting a cone with a plane. In analytic geometry, a conic may be defined as a plane algebraic curve of degree 2...

s (that is, with ellipse

Ellipse

In geometry, an ellipse is a plane curve that results from the intersection of a cone by a plane in a way that produces a closed curve. Circles are special cases of ellipses, obtained when the cutting plane is orthogonal to the cone's axis...

s and hyperbola

Hyperbola

In mathematics a hyperbola is a curve, specifically a smooth curve that lies in a plane, which can be defined either by its geometric properties or by the kinds of equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, which are mirror...

s). One end of the segment is the center of the conic section, and it is at right angle

Right angle

In geometry and trigonometry, a right angle is an angle that bisects the angle formed by two halves of a straight line. More precisely, if a ray is placed so that its endpoint is on a line and the adjacent angles are equal, then they are right angles...

s with the semi-major axis

Semi-major axis

The major axis of an ellipse is its longest diameter, a line that runs through the centre and both foci, its ends being at the widest points of the shape...

. It is one of the axes of symmetry for the curve: in an ellipse, the shorter one; in a hyperbola, the one that does not intersect the hyperbola.

Ellipse

The semi-minor axis of an ellipse is one half of the minor axis, running from the center, halfway between and perpendicular to the line running between the foci

Focus (geometry)

In geometry, the foci are a pair of special points with reference to which any of a variety of curves is constructed. For example, foci can be used in defining conic sections, the four types of which are the circle, ellipse, parabola, and hyperbola...

, and to the edge of the ellipse. The minor axis is the longest line segment that runs perpendicular to the major axis.

The semi-minor axis b is related to the semi-major axis

Semi-major axis

The major axis of an ellipse is its longest diameter, a line that runs through the centre and both foci, its ends being at the widest points of the shape...

  through the eccentricity

Eccentricity (mathematics)

In mathematics, the eccentricity, denoted e or \varepsilon, is a parameter associated with every conic section. It can be thought of as a measure of how much the conic section deviates from being circular.In particular,...

  and the semi-latus rectum 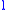, as follows:

.

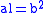The semi-minor axis of an ellipse is the geometric mean

Geometric mean

The geometric mean, in mathematics, is a type of mean or average, which indicates the central tendency or typical value of a set of numbers. It is similar to the arithmetic mean, except that the numbers are multiplied and then the nth root of the resulting product is taken.For instance, the...

 of the maximum and minimum distances 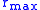and of the ellipse from a focus — that is, of the distances from a focus to the endpoints of the major axis: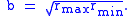


A parabola

Parabola

In mathematics, the parabola is a conic section, the intersection of a right circular conical surface and a plane parallel to a generating straight line of that surface...

can be obtained as the limit of a sequence of ellipses where one focus is kept fixed as the other is allowed to move arbitrarily far away in one direction, keeping l fixed. Thus a and b tend to infinity, a faster than b.

Hyperbola

In a hyperbola, a conjugate axis or minor axis of length 2b, corresponding to the minor axis of an ellipse, can be drawn perpendicular to the transverse axis or major axis, the latter connecting the two vertices (turning points) of the hyperbola, with the two axes intersecting at the center of the hyperbola. The endpoints (0, ±b) of the minor axis lie at the height of the asymptotes over/under the hyperbola's vertices. Either half of the minor axis is called the semi-minor axis, of length b. Denoting the semi-major axis length (distance from the center to a vertex) as a, the semi-minor and semi-major axes' lengths appear in the equation of the hyperbola relative to these axes as follows: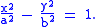


The semi-minor axis and the semi-major axis are related through the eccentricity, as follows:


Note that in a hyperbola b can be larger than a.
http://www.geom.uiuc.edu/docs/reference/CRC-formulas/node27.html

External links

• Semi-minor and semi-major axes of an ellipse With interactive animation