
Star polyhedron
Encyclopedia
In geometry
, a star polyhedron is a polyhedron
which has some repetitive quality of nonconvexity giving it a star-like visual quality.
There are two general kinds of star polyhedron:
Studies of star polyhedra are usually concerned with regular
, uniform
polyhedra, or the duals to the uniform polyhedra. All these stars are of the self-intersecting kind. So some authorities might argue that the concave kind are not proper stars. But the latter usage is sufficiently widespread that it cannot be ignored. The important thing is to be clear which kind you mean.
, or self-intersecting vertex figure
s.
There are four regular star polyhedra, known as the Kepler-Poinsot polyhedra. The Schläfli symbol {p,q} implies faces with p sides, and vertex figures with q sides. Two of them have pentagram
mic {5/2} faces and two have pentagrammic vertex figures.

These images show each form with a single face colored yellow to show the visible portion of that face.
, and their duals
.
The uniform
and dual
uniform star polyhedra are also self-intersecting polyhedra. They may either have self-intersecting faces
, or self-intersecting vertex figure
s or both.
The uniform star polyhedra have regular faces
or regular star polygon faces. The dual uniform star polyhedra have regular faces or regular star polygon vertex figures.
One class is the isohedral figures, which are like the uniform figures, but don't require regular faces.
For example, the complete stellation of the icosahedron can be interpreted as a self-intersecting polyhedron composed of 12 identical faces, each a (9/4) wound polygon. Below is an illustration of this polyhedron with one face drawn in yellow.

s are called star polytopes.
A regular polytope {p,q,r,...,s,t} is a star-polytope if either its facets {p,q,...s}, or its vertex figure {q,r,...,s,t} is a star polytope.
In four dimensions, the 10 regular star polychora, called the Schläfli-Hess polychora. Like the regular star polyhedra, these 10 are all composed of facets which are either one of the five regular Platonic solid
s or one of the four regular star Kepler-Poinsot polyhedra.
For example, the great grand stellated 120-cell, projected orthogonally into 3-space looks like this:
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, a star polyhedron is a polyhedron
Polyhedron
In elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...
which has some repetitive quality of nonconvexity giving it a star-like visual quality.
There are two general kinds of star polyhedron:
- Polyhedra which self-intersect in a repetitive way.
- Concave polyhedra of a particular kind which alternate convex and concave or saddle vertices in a repetitive way.
Studies of star polyhedra are usually concerned with regular
Regular polyhedron
A regular polyhedron is a polyhedron whose faces are congruent regular polygons which are assembled in the same way around each vertex. A regular polyhedron is highly symmetrical, being all of edge-transitive, vertex-transitive and face-transitive - i.e. it is transitive on its flags...
, uniform
Uniform polyhedron
A uniform polyhedron is a polyhedron which has regular polygons as faces and is vertex-transitive...
polyhedra, or the duals to the uniform polyhedra. All these stars are of the self-intersecting kind. So some authorities might argue that the concave kind are not proper stars. But the latter usage is sufficiently widespread that it cannot be ignored. The important thing is to be clear which kind you mean.
Regular star polyhedra
The regular star polyhedra, are self-intersecting polyhedra. They may either have self-intersecting facesFace (geometry)
In geometry, a face of a polyhedron is any of the polygons that make up its boundaries. For example, any of the squares that bound a cube is a face of the cube...
, or self-intersecting vertex figure
Vertex figure
In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...
s.
There are four regular star polyhedra, known as the Kepler-Poinsot polyhedra. The Schläfli symbol {p,q} implies faces with p sides, and vertex figures with q sides. Two of them have pentagram
Pentagram
A pentagram is the shape of a five-pointed star drawn with five straight strokes...
mic {5/2} faces and two have pentagrammic vertex figures.

These images show each form with a single face colored yellow to show the visible portion of that face.
Uniform and dual uniform star polyhedra
There are many uniform star polyhedra including two infinite series, of prisms and of antiprismsPrismatic uniform polyhedron
In geometry, a prismatic uniform polyhedron is a uniform polyhedron with dihedral symmetry. They exist in two infinite families, the uniform prisms and the uniform antiprisms...
, and their duals
Dual polyhedron
In geometry, polyhedra are associated into pairs called duals, where the vertices of one correspond to the faces of the other. The dual of the dual is the original polyhedron. The dual of a polyhedron with equivalent vertices is one with equivalent faces, and of one with equivalent edges is another...
.
The uniform
Uniform polyhedron
A uniform polyhedron is a polyhedron which has regular polygons as faces and is vertex-transitive...
and dual
Dual polyhedron
In geometry, polyhedra are associated into pairs called duals, where the vertices of one correspond to the faces of the other. The dual of the dual is the original polyhedron. The dual of a polyhedron with equivalent vertices is one with equivalent faces, and of one with equivalent edges is another...
uniform star polyhedra are also self-intersecting polyhedra. They may either have self-intersecting faces
Face (geometry)
In geometry, a face of a polyhedron is any of the polygons that make up its boundaries. For example, any of the squares that bound a cube is a face of the cube...
, or self-intersecting vertex figure
Vertex figure
In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...
s or both.
The uniform star polyhedra have regular faces
Regular polygon
A regular polygon is a polygon that is equiangular and equilateral . Regular polygons may be convex or star.-General properties:...
or regular star polygon faces. The dual uniform star polyhedra have regular faces or regular star polygon vertex figures.
Examples
| Uniform polyhedron Uniform polyhedron A uniform polyhedron is a polyhedron which has regular polygons as faces and is vertex-transitive... |
Dual polyhedron Dual polyhedron In geometry, polyhedra are associated into pairs called duals, where the vertices of one correspond to the faces of the other. The dual of the dual is the original polyhedron. The dual of a polyhedron with equivalent vertices is one with equivalent faces, and of one with equivalent edges is another... |
|---|---|
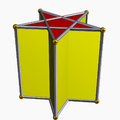 The pentagrammic prism Pentagrammic prism In geometry, the pentagrammic prism is one in an infinite set of nonconvex prisms formed by square sides and two regular star polygon caps, in this case two pentagrams.This polyhedron is identified with the indexed name U78 as a uniform polyhedron.... is a prismatic star polyhedron Prismatic uniform polyhedron In geometry, a prismatic uniform polyhedron is a uniform polyhedron with dihedral symmetry. They exist in two infinite families, the uniform prisms and the uniform antiprisms... . It is composed of two pentagram Pentagram A pentagram is the shape of a five-pointed star drawn with five straight strokes... faces connected by five intersecting square Square (geometry) In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles... faces. |
 The pentagrammic dipyramid is also a star polyhedron, representing the dual to the pentagrammic prism. It is face-transitive, composed of 10 intersecting isoceles triangles. |
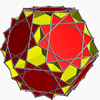 The great dodecicosahedron Great dodecicosahedron In geometry, the great dodecicosahedron is a nonconvex uniform polyhedron, indexed as U63. Its vertex figure is a crossed quadrilateral.It has a composite Wythoff symbol, 3 5/3 |, requiring two different Schwarz triangles to generate it: and .Its vertex figure 6.10/3.6/5.10/7 is also ambiguous,... is a star polyhedron, constructed from a single vertex figure Vertex figure In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:... of intersecting hexagonal and decagrammic, {10/3}, faces Face (geometry) In geometry, a face of a polyhedron is any of the polygons that make up its boundaries. For example, any of the squares that bound a cube is a face of the cube... . |
 The great dodecicosacron Great dodecicosacron In geometry, the great dodecicosacron is the dual of the great dodecicosahedron . It has 60 intersecting bow-tie-shaped faces.- External links :*... is the dual to the great dodecicosahedron. It is face-transitive, composed of 60 intersecting bow-tie shaped quadrilateral Quadrilateral In Euclidean plane geometry, a quadrilateral is a polygon with four sides and four vertices or corners. Sometimes, the term quadrangle is used, by analogy with triangle, and sometimes tetragon for consistency with pentagon , hexagon and so on... faces. |
Other star polyhedra
Beyond the forms above, there are unlimited classes of self-intersecting (star) polyhedra.One class is the isohedral figures, which are like the uniform figures, but don't require regular faces.
For example, the complete stellation of the icosahedron can be interpreted as a self-intersecting polyhedron composed of 12 identical faces, each a (9/4) wound polygon. Below is an illustration of this polyhedron with one face drawn in yellow.

Star polytopes
Higher dimensional intersecting polytopePolytope
In elementary geometry, a polytope is a geometric object with flat sides, which exists in any general number of dimensions. A polygon is a polytope in two dimensions, a polyhedron in three dimensions, and so on in higher dimensions...
s are called star polytopes.
A regular polytope {p,q,r,...,s,t} is a star-polytope if either its facets {p,q,...s}, or its vertex figure {q,r,...,s,t} is a star polytope.
In four dimensions, the 10 regular star polychora, called the Schläfli-Hess polychora. Like the regular star polyhedra, these 10 are all composed of facets which are either one of the five regular Platonic solid
Platonic solid
In geometry, a Platonic solid is a convex polyhedron that is regular, in the sense of a regular polygon. Specifically, the faces of a Platonic solid are congruent regular polygons, with the same number of faces meeting at each vertex; thus, all its edges are congruent, as are its vertices and...
s or one of the four regular star Kepler-Poinsot polyhedra.
For example, the great grand stellated 120-cell, projected orthogonally into 3-space looks like this:
See also
- Star polygon
- StellationStellationStellation is a process of constructing new polygons , new polyhedra in three dimensions, or, in general, new polytopes in n dimensions. The process consists of extending elements such as edges or face planes, usually in a symmetrical way, until they meet each other again...
- Polyhedral compoundPolyhedral compoundA polyhedral compound is a polyhedron that is itself composed of several other polyhedra sharing a common centre. They are the three-dimensional analogs of polygonal compounds such as the hexagram....
- List of uniform polyhedra
- Uniform star polyhedron/Uniform polyhedra by Wythoff constructionUniform star polyhedron/Uniform polyhedra by Wythoff constructionAccording to , there are 4 spherical triangles with angles π/p, π/q, π/r, where are integers:# - Dihedral# - Tetrahedral# - Octahedral# - Icosahedral...


