
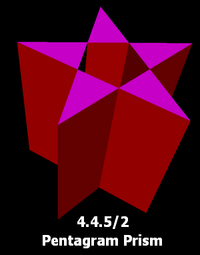
Pentagrammic prism
Encyclopedia
In geometry
, the pentagrammic prism is one in an infinite set of nonconvex prisms
formed by square sides and two regular star polygon caps, in this case two pentagram
s.
This polyhedron is identified with the indexed name U78 as a uniform polyhedron
.
It is a special case of a right prism with a pentagram as base, which in general has rectangular non-base faces.
Note that the pentagram face has an ambiguous interior because it is self-intersecting. The central pentagon region can be considered interior or exterior depending on how interior is defined. One definition of interior is the set of points that have a ray that crosses the boundary an odd number of times to escape the perimeter.
In either case, it is best to show the pentagram boundary line to distinguish it from a concave decagon.
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, the pentagrammic prism is one in an infinite set of nonconvex prisms
Prism (geometry)
In geometry, a prism is a polyhedron with an n-sided polygonal base, a translated copy , and n other faces joining corresponding sides of the two bases. All cross-sections parallel to the base faces are the same. Prisms are named for their base, so a prism with a pentagonal base is called a...
formed by square sides and two regular star polygon caps, in this case two pentagram
Pentagram
A pentagram is the shape of a five-pointed star drawn with five straight strokes...
s.
This polyhedron is identified with the indexed name U78 as a uniform polyhedron
Uniform polyhedron
A uniform polyhedron is a polyhedron which has regular polygons as faces and is vertex-transitive...
.
It is a special case of a right prism with a pentagram as base, which in general has rectangular non-base faces.
Note that the pentagram face has an ambiguous interior because it is self-intersecting. The central pentagon region can be considered interior or exterior depending on how interior is defined. One definition of interior is the set of points that have a ray that crosses the boundary an odd number of times to escape the perimeter.
In either case, it is best to show the pentagram boundary line to distinguish it from a concave decagon.
Gallery
 An alternative representation with hollow centers to the pentagrams. |
 The pentagrammic dipyramid is the dual Dual polyhedron In geometry, polyhedra are associated into pairs called duals, where the vertices of one correspond to the faces of the other. The dual of the dual is the original polyhedron. The dual of a polyhedron with equivalent vertices is one with equivalent faces, and of one with equivalent edges is another... to the Pentagrammic prism |
External links
- http://www.mathconsult.ch/showroom/unipoly/78.html
- http://bulatov.org/polyhedra/uniform/u03.html
- Paper model of pentagrammic prism
- http://www.math.technion.ac.il/~rl/kaleido/data/03.html
- http://home.comcast.net/~tpgettys/nonconvexprisms.html
- http://www.ac-noumea.nc/maths/amc/polyhedr/no_conv5_.htm
- Paper Model (net) Pentagrammic Prism

